
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Московский государственный авиационный институтСодержание книги Поиск на нашем сайте
Московский государственный авиационный институт Кафедра прикладной информатики
Лекции по дисциплине: “МЕТОДЫ ОПТИМИЗАЦИИ ”
Содержание:
- понятие САПР - процесс оптимизации
- аналитический способ - численный способ
- метод “золотого сечения”
- метод деление интервала пополам - метод Ньютона (метод касательной)
- приемущества - недостатки
- метод наискорейшего спуска - анализ метода - метод Ньютона - недостатки метода Ньютона
- метод исключения - метод множителей Лагранжа
- методы решения НЛП
Основные понятия. САПР – система автоматизированного проектирования. Проектирование сложный процесс, направленный на разработку отдельного объекта.
Способ уменьшения время проектирования – уменьшение числа разработчиков. Система – совокупность людей, задач и программ, которые взаимосвязаны друг с другом. Оптимизация – от латинского слова «оптимус» - наилучший – поиск наилучшего, поиск наилучшего проектного изделия.
Процесс оптимизации.
Имеется задача. Для решения задачи нужно формализовать объект и представить его в виде математической модели.
Модели: - физические; - геометрические (фотография, рисунок); - математические.
Математическая модель, та которая определена с помощью математических формализмов. Математическая модель не является точной, а является идеализацией. Модель характеризуется параметрами, которые могут быть и числовыми Определение параметров состояния - задача моделирования. Определение переменных проектирования – задачи проектирования или задачи оптимизации.
Допустим имеются 2 переменные
R G множество допустимых
p1 недопустимое решение – не удовлетворяющее наложенным ограничениям
Плоскость множества возможных вариантов, на нее могут быть наложены ограничения.
Отображение множества
2 вида задач оптимизации: - максимизации; - минимизации.
Для оптимизационного решения задачи требуется:
Численные методы.
а
Если из того что
Методы одномерного поиска.
Разобьем
искомый минимум
В результате остается интервал меньшего размера, к которому применяется тот же метод, и находим еще один интервал, в конце находим интервал с заведомо нужной точкой.
Интервал неопределенности – интервал, в котором заведомо находится точка минимума. Наиболее эффективное разбиение – двумя точками на 3 равных отрезка.
1) 2)
N=2n, где n – число шагов, N – число вычислений (мера эффективности данного решения).
Метод золотого сечения.
Точки должны быть расположены на равном расстоянии.
число итераций растет как логарифм функции.
Безусловная оптимизация.
Целевая функция зависит от нескольких переменных f(х1, х2, …, хn)® min. Т.к. нет дополнительных условий накладывающихся на переменные – безусловная оптимизация.
Функции 2-х переменных
x2 x1
Условия определяющие точку минимума – необходимо проанализировать поведение функции в некоторой точке.
х2
Часто под окрестностью подразумевают шар.
Рассмотрим вспомогательное построение:
линейное векторное
x2 x1
Скалярное произведение векторов
Допустим, что:
Тогда:
Допустим, что имеется 2 вектора:
Чтобы задать направление, мы задаем вектор.
Нормированный вектор имеет тоже самое направление, но
Допустим, что задан нормированный вектор
Возвращаемся к функции 2-х переменных:
Отбрасываем члены
Вектор
grad – вектор, в сторону которого функция изменяется более быстро. Антиградиент – grad направленный в другую сторону (-grad).
Допустим что мы совершаем малое перемещение * - если под прямым углом, то не изменяется; * - если под тупым углом, то приводит к уменьшению функции.
1. строим поверхности
x
2. Идет построение в плоскости х1 и х2. Берут точку – определяющую значение аргумента. Находят точку в которой функция имеет тоже самое значение, в результате получаем линию в которой функция имеет постоянное значение – изолиния (линия уровня).
Вектор grad составляет прямой угол с изолинией. Вернемся к формуле:
Квадратичная аппроксимация. (или квадратичное приращение)
Линейное отображение:
1. свойство аддитивности - 2. свойство однородности -
Линейное отображение можно задать матрицей:
п
2 задачи: - решение системы уравнений
и обратное отображение – найти х А-1 – обратное отображение;
другой матрицы - нахождение собственных значений
Используя матрицу можно найти более сложную функцию:
Рассмотрим подробнее. Есть матрица:
А и А/ определяют одну и ту же квадратичную форму следовательно значения этой формы не однозначно. Если по заданной квадратичной форме найдем симметрию, то она будет однозначная.
Без ограничения общности можно считать, что матрица определяющая квадратичную форму является симметричной.
Вернемся к квадратичной форме:
Рассмотрим функцию 2-го порядка:
Допустим, что
Допустим, что
Рассмотрим п -мерный случай. Квадратичная форма называется положительно определенной областью если она не отрицательная.
Рассмотрим 2-мерное пространство:
Рассмотрим разложение функции 2-х переменных в ряд Тейлора:
квадратичная матрица задается матрицей Н
матрица составленная из членов 2-го порядка
Матрица Н – матрица Гесса.
Если матрица (матрица Гесса) в точке локального экстремума положительно определена, то это точка – локального минимума, если матрица отрицательно определена, то это точка – локального максимума, а если не определена – седловые точки.
Седловая точка
Минимизируем:
Найти частные производные: 1. 2.
Эта система позволяет найти все точки экстремума:
Допустим, что
Необходимые условия – помогают охарактеризовать искомую точку:
Н ³ 0 – локальный минимум; Н £ 0 – локальный максимум; Н – не определена – седловая точка.
Для поиска используют численные методы.
Постановка: Требуется Есть черный ящик, который по заданным значениям х позволяет вычислить значение функции.
Методы прямого поиска.
Выбираем точку где хуже. В окрестности существующей точки выбираем точку с меньшим значением, опять в ее окрестности есть точки с меньшим значением и т.д.
В таком виде этот метод не эффективен. Пример: Шаг по х1 берем больше, а по х2 – сохраняем. Поскольку мы свободны в выборе точек, то можно менять шаг и направление. Методы:
Преимущества метода прямого поиска:
Недостатки:
Этот метод применим в простых случаях, когда эти недостатки себя не проявляют.
Метод координатного спуска.
Этот процесс повторяют до тех пор пока следующая точка не окажется близка к точке приближения.
Градиентные методы. Метод наискорейшего спуска.
Рассмотрим grad целевой функции. Движение по направлению вектора под острым углом будет приводить к уменьшению целевой функции, а движение против направления функции к увеличению целевой функции. Разумно за направление движения принять сам вектор – grad f.
Для выбора расстояния нужно применить метод одномерной оптимизации. Прекратить поиск, когда величина grad f станет достаточно малой. Этот метод гарантирует, что найдена либо точка локального минимума, либо седловая точка.
Анализ метода.
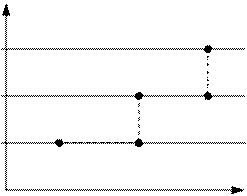
В случае когда масштаб выбирается следующим образом (линии уровня вытянуты).
Траектория
Если линии уровня
Метод Ньютона.
Метод исключения Численное решение:
g(x)
В каждый момент линия уровня будет касаться прямой условного локального min. Если в окрестности заданной точки, удовлетворяющей всем значениям равенства, значение функции больше, чем в точке, то эта точка – есть точка условного локального min. Пример:
(a,x)=0
Если (a1x)=b
Допустим,
Прямая будет проходить через некоторую точку удовлетворяющую условию и Для n переменных Рассмотрим i-ое ограничение:
При добавлении еще одного условия, уменьшаются размерности. В конечном итоге получится пространство n-m.
Для двух переменных возможно 2 случая:
В случае 2 это не точка минимума, а седловая точка.
Рассмотрим точку 3-х переменных:
Пусть существует 2 ограничения:
Рассмотрим опять случай 3-х переменных: Точка минимума должна принадлежать пересечению плоскостей. Необходимое условие – вектор антиградиента должен составлять угол 90 градусов с прямой пересечения плоскостей. Для п -мерного случая имеется п переменных следовательно рассматривая каждое ограничение, получаем п-1 гиперплоскость следовательно рассмотрев т ограничений получим п-т гиперплоскость (т<п).
Если вектор grad (п -мерный) будет ортогонален п-т – пространству.
Допустим имеется п-1 пространство, п -мерный вектор может принадлежать ему или нет. Пусть вектор не принадлежит данному подпространству следовательно его можно разложить на 2 вектора – один который принадлежит подпрост
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.87 (0.01 с.) |

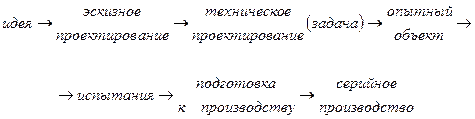
 . Их часть может характеризовать состояние объекта – параметры состояния
. Их часть может характеризовать состояние объекта – параметры состояния 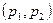 , а другие могут относиться к процессу проектирования – переменные проектирования
, а другие могут относиться к процессу проектирования – переменные проектирования  .
. . Задавая конкретные значения получаем точку.
. Задавая конкретные значения получаем точку.
 R – множество чисел
R – множество чисел вариантов
вариантов


 p2 допустимое решение
p2 допустимое решение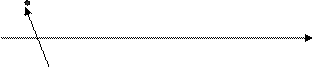
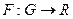 - целевая функция позволяет формировать критерий для сравнения различных решений.
- целевая функция позволяет формировать критерий для сравнения различных решений. Пусть функция
Пусть функция 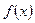 задана на интервале
задана на интервале  , при этом существует такая точка
, при этом существует такая точка  , что на
, что на 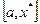 – монотонно убывает, а на
– монотонно убывает, а на  – монотонно возрастает, то функция унимодальная.
– монотонно возрастает, то функция унимодальная.
 следует, что
следует, что  , то функция называется монотонно возрастающей. Если из того что
, то функция называется монотонно возрастающей. Если из того что  следует, что
следует, что  , то функция называется монотонно убывающей.
, то функция называется монотонно убывающей. и вычислим значение функции в каждой точке.
и вычислим значение функции в каждой точке.


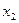







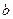

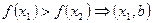
 - после выполнения n шагов сокращение исходного интервала
- после выполнения n шагов сокращение исходного интервала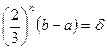
 - точность с которой надо найти решение задачи.
- точность с которой надо найти решение задачи.







 а b
а b
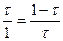 ;
;  ;
;  ;
; ;
; 
 а
а




 - величина сокращения на каждом шаге
- величина сокращения на каждом шаге
 f(x1,x2)
f(x1,x2)


 х2
х2
 пространство
пространство

 (х1,х2,х3)
(х1,х2,х3)
 , где
, где  - длина вектора (норма вектора),
- длина вектора (норма вектора),  - угол между векторами.
- угол между векторами.
 S
S

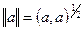
 ,
, 
 ;
; 






 a
a



 Нормируем вектор
Нормируем вектор 

 , длина.
, длина.





 Скалярное произведение равно 0, тогда года
Скалярное произведение равно 0, тогда года  прямой.
прямой.

 , приращение будет более точным.
, приращение будет более точным. х2
х2














 Þ
Þ  - формула Тейлора.
- формула Тейлора.


 х2
х2 

 - производная по направлению (вдоль данного направления)
- производная по направлению (вдоль данного направления) - направление ряда равное направлению grad (£ 0).
- направление ряда равное направлению grad (£ 0). х2
х2
 grad f
grad f
 f(x)
f(x)



 х2
-grad f
х2
-grad f
 - локальный минимум (или максимум). Точки локального экстремума.
- локальный минимум (или максимум). Точки локального экстремума.
 .
.

 y
y


 х1 х1
- изолиния
х1 х1
- изолиния
 z
z

 изолиния
изолиния



 - линейное отображение, если:
- линейное отображение, если: ;
;

 т
т

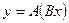 ;
;  ;
; - основная формула
- основная формула


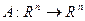 отображение
отображение 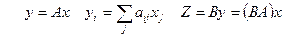

 следовательно строки матрицы ортогональны столбцам
следовательно строки матрицы ортогональны столбцам - квадратичная форма.
- квадратичная форма. - функция нескольких переменных
- функция нескольких переменных 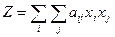 .
.
 - квадратичная форма
- квадратичная форма

 ;
; ;
; 


 , матрица диагональная.
, матрица диагональная.

 Эллипсы
Эллипсы
 Эллиптический парабалоид
Эллиптический парабалоид





 Седло
Седло
 . Тогда вся картина просто повернется на некоторый угол по оси Z.
. Тогда вся картина просто повернется на некоторый угол по оси Z. , причем обращается в ноль, в том случае если х = 0 (
, причем обращается в ноль, в том случае если х = 0 ( ). Этот случай соответствует эллиптическому параболоиду.
). Этот случай соответствует эллиптическому параболоиду. ,
, 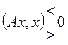 соответствует п -мерному эллиптическому гиперболоиду (п -мерное седло)
соответствует п -мерному эллиптическому гиперболоиду (п -мерное седло)



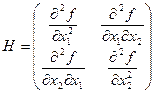 - матрица симметрична
- матрица симметрична - определение матрицы Гесса
- определение матрицы Гесса Локальный max или min
Локальный max или min
 (grad = 0);
(grad = 0);

 . Надо составить функцию второго порядка и подставить
. Надо составить функцию второго порядка и подставить  и посмотреть их.
и посмотреть их.
 , где х – вектор
, где х – вектор  - т.к. нет ограничений задача безусловной оптимизации.
- т.к. нет ограничений задача безусловной оптимизации.





 - некоторое приближение полученное после к – итераций;
вычислить значение точки в окрестности точки
- некоторое приближение полученное после к – итераций;
вычислить значение точки в окрестности точки 

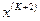






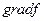





 - окружности, то приходим сразу в точку локального минимума.
- окружности, то приходим сразу в точку локального минимума.

 - один постоянный член любой точки данной функции является оптимальным – тривиальный случай;
- один постоянный член любой точки данной функции является оптимальным – тривиальный случай;
 (возможно бесконечное уменьшение и увеличение)
(возможно бесконечное уменьшение и увеличение)

 точка min должна лежать на прямой.
точка min должна лежать на прямой.







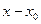


 , Ax=b
, Ax=b ,
, 
 x - все вектора, лежащие
x - все вектора, лежащие 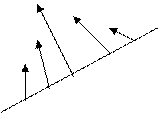 1.
1.
 2.
2.


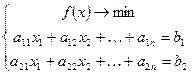

 все ограничения
независимы
все ограничения
независимы



