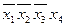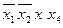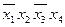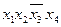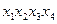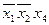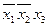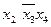Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение к СКНФ. Алгоритм приведения.
Рассматриваем только те строки таблицы, где формула принимает значение 0. Каждой такой строке соответствует дизъюнкция всех переменных (без повторений). Причем аргумент, принимающий значение 0, берется без отрицания, значение 1 – с отрицанием. Наконец, образуют конъюнкцию полученных дизъюнкций. Пример 30. Построить СКНФ для данных формул логики высказываний. 1. 2. Решение.
Таблица 15
Рассматриваем только наборы, на которых формула принимает значение ноль. СКНФ (0): № 0, 1, 2, 3, 6:
Таблица 16
СКНФ (0): № 0, 1, 2:
2.2. Булевы функции 2.2.1. Представление булевой функции формулой логики высказываний Определение. Булевой функцией f(x1, x2, …, xn) называется n-местная функция, аргументы которой принимают значения во множестве {0, 1} и сама функция принимает значения в этом же множестве. Всякую булеву функцию от n переменных можно задать таблицей из 2n строк, в которой в каждой строке записывают одну из оценок списка переменных, принимающих значение 0 или 1. Пример 31. Для n=3 булеву функцию можно задать таблицей 17. Таблица 17
Используется также задание булевой функции в виде двоичного слова, длина которого зависит от числа переменных. Пример 32. Пусть задана булева функция от трех переменных (табл. 18). Тогда число наборов Таблица 18
Номера наборов всегда нумеруются, начиная с нуля, в таблице приведено стандартное расположение всех наборов функции трех переменных (обратите внимание, что каждый набор представляет собой двоичный код числа, равный номеру соответствующего набора). Первые четыре столбца одинаковы для всех булевых функций от трех переменных. Столбец значений функции задается или вычисляется.
Эту же функцию можно записать f(х1, х2, х3)=00101101. Существует ровно Утверждение. Каждой формуле логики высказываний соответствует некоторая булева функция. Пример 33. Построить все булевы функции, зависящие от двух переменных. Решение. Поскольку n=2, различных булевых функций от двух переменных существует ровно 16 (табл. 19). Таблица 19
Теорема. Пусть f(x1, x2, …, xk) k-местная булева функция. Если f не равна тождественно нулю, то существует такая формула F, зависящая от списка переменных x1, x2, …, xn и находящаяся в СДНФ относительно этого списка, что F выражает собой функцию f. Формула F определена однозначно с точностью до перестановки дизъюнктивных членов. Теорема 2. Пусть f(x1, x2, …, xk) k-местная булева функция. Если f не равна тождественно единице, то существует такая формула F, зависящая от списка переменных x1, x2, …, xk и находящаяся в СКНФ относительно этого списка, что F выражает собой функцию f. Формула F определена однозначно с точностью до перестановки конъюнктивных членов. Поскольку каждая булева функция представима в виде формулы логики высказываний, то принцип построения СДНФ и СКНФ сохраняется такой же как и для формул логики высказываний. Пример 34. Построить СКНФ и СДНФ булевой функции f(x1, x2, x3)= 00101110. Решение. Строим таблицу значений функции (табл. 20): Таблица 20
СКНФ (0): № 0, 1, 3, 7
СДНФ (1): № 2, 4, 5, 6
2.2.2. Минимизация нормальных форм Выше было сказано, что произвольная булева функция может быть представлена формулой в дизъюнктивной и конъюнктивной нормальной форме. Равносильными преобразованиями можно получить формулу, содержащую меньшее, чем исходная, число переменных. Определение. Минимальной ДНФ (МДНФ) функции f(x1, x2, …, xn) называется ДНФ, реализующая функцию f и содержащая минимальное число символов переменных по сравнению со всеми другими ДНФ, реализующими функцию f. Минимальную ДНФ данной формулы можно найти, перебрав конечное число равносильных ей ДНФ и выбрав среди них ту, которая содержит минимальное число переменных. Однако при большом числе переменных такой перебор практически невыполним. Существуют эффективные способы нахождения минимальной ДНФ. Рассмотрим два из них. Каждый из рассмотренных ниже методов состоит из двух этапов: · построение сокращенной ДНФ; · построение матрицы покрытий. Построение МДНФ. Определение. Если для всякого набора а = (а1, а2, …, an) значений переменных условие g(a) = 1 влечет f(a) = 1, то функция g называется частью функции f (или функция f накрывает функцию g ). Если при этом для некоторого набора с = (с1, с2, …, сn)функция g(c)=1, то говорят, что функция g накрывает единицу функции f на наборе с (или что g накрывает конституенту единицы Конституента единицы функции f есть часть функции f, накрывающая единственную единицу функции f. Определение. Элементарная конъюнкция К называется импликантом функции f, если для всякого набора а = (а1, а2, …, an) из 0 и 1 условие К(а)=1 влечет f(a)=1. Определение. Импликант К функции f называется простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не импликант функции f. Всякий импликант функции f есть часть функции f. Теорема. Всякая функция реализуется дизъюнкцией всех своих простых импликант. Определение. Сокращенная ДНФ функции f есть дизъюнкция всех простых импликант функции f. Утверждение. Всякая функция f реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ. Теорема (Куайна). Если в СДНФ функции f провести все операции неполного склеивания, а затем все операции поглощения и удаления дублирующих членов, то в результате получится сокращенная ДНФ функции f. 2.2.2.1. Алгоритм Куайна построения сокращенной ДНФ 1. Получить СДНФ функции. 2. Провести все операции неполного склеивания. 3. Провести все операции поглощения. Пример 35. Минимизировать функцию f=1111010010101111. Решение. 1. Строим таблицу значения для данной функции (табл. 20). Строим СДНФ функции. При этом слагаемые нумеруем и записываем в столбец (табл. 21). Таблица 20
СДНФ (1): № 0, 1, 2, 3, 5, 8, 10, 12, 13, 14, 15.
Таблица 21
2. Проводим все операции неполного склеивания. Первый этап склеивания (табл. 22): Таблица 22
В первом этапе склеивания участвовали все слагаемые СДНФ, значит, ни одно из исходных слагаемых не войдут в сокращенную ДНФ. После первого этапа склеивания (и возможных поглощений) получаем, что
Пронумеруем дизъюнктивные члены в полученной ДНФ в порядке их следования от 1 до 15 (табл. 23). Второй этап склеивания: Таблица 23
В процедуре склеивания на втором этапе не принимали участие слагаемые № 5, 8 с предыдущего шага, поэтому после второго этапа склеивания и последующих поглощений получаем, что
Поскольку дальнейшее склеивания невозможны, то это и будет сокращенная ДНФ исходной функции.
2.2.2.2. Построение сокращенной ДНФ в классе дизъюнктивных нормальных форм Этот метод не отличается большой эффективностью, но он прост для изложения и не требует введения дополнительных понятий. Пусть булева функция задана таблицей истинности или СДНФ. Минимизирующая карта булевой функции представляет собой квадратную матрицу 2n´2n, где n – число переменных. Первые столбцы отводят для аргументов, дальнейшие – для их всевозможных конъюнкций по 2, по 3 и т. д. сомножителей, предпоследний - для конъюнкции всех аргументов, последний – для значений функции. Шаг 1. Столбцы для аргументов, как обычно в таблицах истинности, заполняются всевозможными наборами 0 и 1. В столбцах для конъюнкций проставляются десятичные значения двоичных чисел, соответствующих наборам значений аргументов. Последний столбец заполняется соответственно значению функции. Далее работа чередуется по строкам, по столбцам. Шаг 2. Вычеркиваются строки, в которых функция обращается в нуль. Шаг 3. В каждом столбце из сохранившихся чисел вычеркивают те, равные которым уже вычеркнуты в этом столбце на предыдущем шаге.
Шаг 4. В сохранившихся строках выбирают «значения» наименьших по числу множителей конъюнкций (включая и конъюнкции с одним множителем – переменные) и обводят их кружочками. Шаг 5. Если в одном столбце обведено несколько одинаковых чисел, то вычеркивают все, кроме одного. Шаг 6. С помощью оставшихся обведенных чисел образуют конъюнкции. Для этого переводят каждое число в двоичную систему. Переменную, которой соответствует 1, берут сомножителем без отрицания, которой соответствует 0 – с отрицанием. Шаг 8. Составляют дизъюнкцию полученных конъюнкций. В результате получаем сокращенную ДНФ функции. Пример 36. Построить сокращенную ДНФ для функции f=11100101. Решение. 1.Строим минимизационную карту (табл. 24): Таблица 24
2. Вычеркиваем строки, в которых функция обращается в нуль (табл. 25): Таблица 25
3. В каждом столбце из сохранившихся чисел вычеркиваем те, равные которым уже вычеркнуты в этом столбце на предыдущем шаге (табл. 26): Таблица 26
4. В сохранившихся строках выбираем «значения» наименьших по числу множителей конъюнкций (включая и конъюнкции с одним множителем – переменные) и обводим их (табл. 27): Таблица 27
5. Если в одном столбце обведено несколько одинаковых чисел, то вычеркиваем все, кроме одного (табл. 28): Таблица 28
6. С помощью оставшихся обведенных чисел образуем конъюнкции. Для этого переводим каждое число в двоичную систему. Переменную, которой соответствует 1, берем сомножителем без отрицания, 0 – с отрицанием. Составляем дизъюнкцию полученных конъюнкций. Сокращенная ДНФ имеет вид:
Пример 37. Построить сокращенную ДНФ функции f=1111010010101111 с использованием минимизационной карты. Решение. Строим минимизационную карту (табл. 29) и пошагово выполняем алгоритм. Шаг 1. Таблица 29
Шаг 2. Вычеркиваем строки, в которых функция обращается в нуль (табл. 30): Таблица 30
Шаг 3. В каждом столбце из сохранившихся чисел вычеркиваем те, равные которым уже вычеркнуты в этом столбце на предыдущем шаге (табл. 31): Таблица 31
Шаг 4. В сохранившихся строках выбираем «значения» наименьших по числу множителей конъюнкций (включая и конъюнкции с одним множителем – переменные) и обводим их (табл. 32): Таблица 32
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 768; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.242 (0.194 с.) |
 .
.

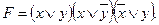
 .
. различных булевых функций от n переменных. Константы 0 и 1 считают нуль-местными булевыми функциями.
различных булевых функций от n переменных. Константы 0 и 1 считают нуль-местными булевыми функциями.
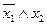



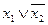
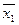



 функции f).
функции f).