
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет дискретной математикиСтр 1 из 8Следующая ⇒
ВВЕДЕНИЕ Дискретная математика – самостоятельное направление современной математики. Она изучает математические модели объектов, процессов, зависимостей, существующих в реальном мире, с которыми имеют дело в технике, информатике и других областях знаний.
ПРЕДМЕТ ДИСКРЕТНОЙ МАТЕМАТИКИ Дискретная математика, или дискретный анализ – область математики, которая занимается исследованием структур и задач на конечных множествах. Специфика задач дискретной математики в первую очередь предполагает отказ от основных понятий классической математики – предела и непрерывности. Поэтому для задач дискретной математики обычные средства классического анализа являются вспомогательными. Дискретная и непрерывная математика взаимно дополняют друг друга. Понятия и методы одной часто используются в другой. Один и тот же объект может рассматриваться с двух точек зрения. Дискретная математика предлагает: · универсальные средства (языки) формализованного представления; · способы корректной переработки информации; · возможности и условия перехода с одного языка описания явлений на другой с сохранением содержательной ценности моделей. Сегодня дискретная математика является важным звеном математического образования. Умение проводить анализ, композицию и декомпозицию информационных комплексов и информационных процессов – обязательное квалификационное требование к специалистам в области информатики.
Нормальные формы Определение. Элементарной конъюнкцией называется конъюнкция, составленная из попарно различных переменных или отрицаний переменных. Иногда будем допускать в элементарной конъюнкции наличие повторов элементов. Определение. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция попарно различных элементарных конъюнкций. Иногда будем допускать в ДНФ наличие повторов элементов. Пример 25. Следующие формулы находятся в ДНФ: Определение. Элементарной дизъюнкцией называется дизъюнкция, составленная из попарно различных переменных или отрицаний переменных. Иногда будем допускать в элементарной дизъюнкции наличие повторов элементов. Определение. Конъюнктивной нормальной формой (КНФ) называется конъюнкция попарно различных элементарных дизъюнкций.
Иногда будем допускать в КНФ наличие повторов элементов. Пример 26. Следующие формулы находятся в КНФ: Двойственные функции Определение. Двойственной для функции f(x1, x2, …, xn) называется функция
Пример 44. Построить функцию, двойственную данной: 1. f = x Ú y; 2. f = x® y. Решение. 1. 2. Определение. Функция, совпадающая со своей двойственной, называется самодвойственной. Утверждение. Если функция f(x1, x2, …, xn) самодвойственна, то функция Утверждение. Чтобы функция была самодвойственной необходимо и достаточно, чтобы на всяких двух противоположных наборах она принимала разные значения. Противоположными называются те наборы, которые в сумме дают двоичный код числа (2n-1). Пример 45. Выяснить являются ли функции самодвойственными: 1. 2. f = 01110010. Решение. 1. Строим таблицу истинности для данной функции Таблица 55
Так как наборы (0, 0, 0) и (1, 1, 1) являются противоположными, а f(0, 0, 0) = f(1, 1, 1), то данная функция не является самодвойственной. 2. Строим таблицу значений для функции f = 01110001 (табл. 56). Таблица 56
Перечислим пары противоположных наборов: (0, 7), (1, 6), (2, 5), (3, 4). Легко убедиться по таблице, что на всяких двух противоположных наборах функция принимает разные значения. Следовательно, функция является самодвойственной.
Теорема. Класс S = {f | f = f*}самодвойственных функций замкнут относительно суперпозиций.
2.2.3.2. Линейные функции Определение. Арифметические функции в алгебре логики это сложение по модулю два и умножение (конъюнкция). Определение. Многочленом Жегалкина называется многочлен, являющийся суммой константы 0 или 1 и различных одночленов, в которые все переменные входят не выше, чем в первой степени:
Теорема. Всякую булеву функцию можно представить единственным полиномом Жегалкина. Многочлен Жегалкина можно получить различными способами. Остановимся на рассмотрении построения многочлена Жегалкина с помощью треугольника Паскаля. Рассмотрим алгоритм на примере. Пример 46. Построить многочлен Жегалкина для функции f=10011110. Решение. Алгоритм построения многочлена Жегалкина: Шаг 1. Строим таблицу (табл. 57). Первый столбец содержит возможные слагаемые полинома Жегалкина. Нулевому набору всегда соответствует слагаемое 1. Остальным наборам соответствует слагаемое, представляющее собой конъюнкцию переменных, которые на данном наборе принимают значение 1. Следующие n столбцов – всевозможные наборы из 0 и 1, соответствующие переменным. Далее столбец значений функции f. Функция g является вспомогательной, поэтому изначально этот столбец не заполнен. Таблица 57
Шаг 2. Построение треугольника Паскаля. Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю два двух соседних элементов предыдущей строки. Левая сторона треугольника представляет собой значение вспомогательной функции g (табл. 58). Таблица 58
Шаг 3. Построение полинома Жегалкина. В полином войдут только те слагаемые, которым соответствует единица во вспомогательной функции g. Для данной функции многочлен Жегалкина имеет вид: f = 1 + x3 + x2 + x1 x3 + x1 x2 + x1 x2 x3.
Определение. Функция f(x1, x2, …, xn) называется линейной, если многочлен Жегалкина для нее имеет следующий линейный относительно переменных вид: f(x1, x2, …, xn) = a1x1 + … + anxn + an+1, где каждое ai равно 0 или 1. Булева функция из рассмотренного выше примера не является линейной. Теорема. Класс L = {f | f = a0+a1x1+…+anxn, aiÎ{0, 1}} линейных функций замкнут относительно суперпозиций. Монотонные функции Определение. Если a = (a1, …, an) и b = (b1, …, bn) - наборы длины n из 0 и 1, то a £ b, если a1 £ b1, …, an £ bn. Пример 47. Наборы (0, 1, 0) и (1, 1, 0) сравнимы, причем (0, 1, 0) £ (1, 1, 0). Наборы (0, 1) и (1, 0) несравнимы. Также несравнимы наборы (0, 1) и (1, 1, 0). Определение. Функция f(x1, x2, …, xn) называется монотонной, если для всяких наборов a = (a1, …, an) и b = (b1, …, bn) условие a £ b влечет f(a) £ f(b). Утверждение. Функция монотонна тогда и только тогда, когда ее сокращенная ДНФ не содержит отрицаний. Следствие. Функция монотонна тогда и только тогда, когда ее МДНФ не содержит отрицаний. Пример 48. Выяснить, являются ли функции монотонными:
Решение. 1. Сокращенная ДНФ для функции f = 00100110 имеет вид
2. Сокращенная ДНФ для функции f = 00110111 имеет вид Теорема. Класс M = {f | a£ b Þ f(a)£ f(b)} монотонных функций замкнут относительно суперпозиций. 2.2.3.4. Теорема Поста о функциональной полноте Теорема Поста (признак полноты системы булевых функций). Для того чтобы система булевых функций {f1, …, fm} была полной, необходимо и достаточно, чтобы для каждого из пяти функционально замкнутых классов T0, T1, L, M, S нашлась хотя бы одна функция fi из системы, не принадлежащая этому классу. Пример. Выяснить к каким функционально замкнутым классам принадлежит булева функция f=01001110, используя теорему Поста. Решение. Строим таблицу значений и треугольник Паскаля (табл. 59): Таблица 59
Полином Жегалкина имеет вид: f = x3 + x2x3 + x1 + x1 x3.
Сведем полученные данные:
Пример 49. Доказать полноту системы {+, Ú, 1}. Решение. Введем обозначения: f1 = x1 + x2, f2 = x1 Ú x2, f3 = 1. Построим единую таблицу для функций (табл. 60). Таблица 60
Полином Жегалкина:
Поскольку для каждого из пяти функционально замкнутых классов нашлась функция, не принадлежащая этому классу (в каждом столбце имеется хотя бы один минус), то система булевых функций {+, Ú, 1} является полной.
2.2.4. Существенные и несущественные переменные. Производная булевой функции первого порядка. Вес переменной
Определение. Булева функция fÎPn существенно зависит от переменной xi, если существует такой набор значений a1, …, ai-1, ai+1, …, an, что
В этом случае xi называют существенной переменной, в противном случае xi называют несущественной переменной. Определение. Производная первого порядка
где f(x1, x2, …, xi-1, 1, xi+1, …, xn) – единичная остаточная функция; f(x1, x2, …, xi-1, 0, xi+1, …, xn) – нулевая остаточная функция; Å - сумма по модулю 2. Единичная остаточная функция получается в результате приравнивания переменной xi единице, нулевая – приравниванием xi нулю. Определение. Весом производной Утверждение. Чем больше вес производной Пример 50. Определить переменную xi, по которой производная
имеет минимальный (максимальный) вес, т. е. функция f(x1, x2, x3, x4, x5) зависит от нее менее (более) существенно. Решение. Определим вес каждой переменной, найдя сначала соответствующую производную. Имеем
 зависящей от четырех переменных х2, х3, х4, х5, представим 4-мерное пространство с образующими {x2, x3, x4, x5} в виде декартова произведения двух двумерных пространств {x2, x3}´ {x4, x5} с образующими {x2, x3} и {x4, x5} соответственно. Тогда производную зависящей от четырех переменных х2, х3, х4, х5, представим 4-мерное пространство с образующими {x2, x3, x4, x5} в виде декартова произведения двух двумерных пространств {x2, x3}´ {x4, x5} с образующими {x2, x3} и {x4, x5} соответственно. Тогда производную  можно задать в виде двумерной таблицы (табл. 61). Вес производной можно задать в виде двумерной таблицы (табл. 61). Вес производной  равен числу единиц в этой таблице. равен числу единиц в этой таблице.
Итак, Аналогично вычислим вес производных
Таблица 64
Таблица 65
Выяснили, что минимальное значение
2.3. Исчисление высказываний Таблицы истинности позволяют ответить на многие вопросы, касающиеся формул логики высказываний, например на вопрос о тождественной истинности формулы или на вопрос о равносильности двух формул. Однако более сложные вопросы логики высказываний уже не могут быть решены с помощью таблиц истинности. Наряду с алфавитом и правилами построения сложных высказываний – логических формул, языки логики высказываний содержат правила преобразования логических формул. Правила преобразования реализуют общелогические законы и обеспечивают логически правильные рассуждения. Корректность допустимых в логике преобразований является фундаментальным свойством формальной (математической) логики.
Если описание системы (процесса, явления и т.п.) представлено совокупностью сложных высказываний – логических формул, истинных для данной системы (в данной интерпретации ее простых высказываний), то с помощью допустимых преобразований имеющихся логических представлений о системе может быть выполнен их анализ (синтез), могут быть получены новые представления, характеризующие указанную систему (истинные для данной системы) и т.п. Таким образом, с помощью допустимых в логике преобразований появляется возможность получения новых знаний из имеющихся. Определение. Процесс получения новых знаний, выраженных высказываниями, из других знаний, также выраженных высказываниями, называется рассуждением (умозаключением). Исходные высказывания называются посылками (гипотезами, условиями), а получаемые высказывания – заключением (следствием). Логика – это наука о способах доказательства. В логике высказываний все доказательства строятся на отношении порядка, т.е. на отношении, которое существует между причиной и следствием. Отдельные звенья цепи связаны символом импликации «®» при логическом выводе мы будем заменять на символ «Þ», подобно тому, как используются два символа эквивалентности «»» и «=». Во избежании путаницы вместо конъюнкции «Ù» будем использовать символ запятой «,», а вместо дизъюнкции «Ú» - символ точка с запятой «;». Тогда утверждение, которое требуется доказать, в логике высказываний оформляется в виде следующего причинно-следственного отношения: P1, P2, …, Pn-1, Pn Þ C, где Pi – посылка, С – заключение. Условимся формальную запись такого рода называть клаузой. Смысловой текст, отвечающий некоторой конкретной клаузе, будем называть её легендой. Пример 51. Для данной легенды построить соответствующую клаузу: «Если фирма приглашает на работу крупного специалиста в области новейшей технологии, то она считает ее привлекательной и разворачивает работы по изменению технологии производства своего традиционного продукта или начинает разработку нового продукта. Конкурирующая фирма пригласила на работу крупного специалиста в области новейшей технологии. Следовательно, она разворачивает работы по изменению технологии производства выпускаемого продукта или разработке нового продукта». Решение. Выделим простые высказывания и введем обозначения: А – «фирма приглашает на работу крупного специалиста в области новейшей технологии»; B – «фирма считает данную новейшую технологию привлекательной»; С – «фирма разворачивает работу по изменению технологии производства своего традиционного продукта»; D - «фирма начинает разработку нового продукта». С учетом принятых обозначений умозаключение примет вид: «Если А, то В и (С или D). А. Следовательно, С или D.» Используя логические связки, получим окончательно: ((А®(ВÙ(СÚD)))ÙA)Þ(CÚD). Используя равносильности логики высказываний получаем:
Если клауза верна, то она является некоторой логической теоремой. В логике высказываний существует несколько способов доказательств теорем. В логике высказываний существуют аксиоматический и конструктивный подходы доказательств логических выражений. Рассмотренные ниже метод Вонга и метод резолюций относится к смешанной стратегии доказательств.
2.3.1. Основные схемы логически правильных рассуждений Приведем примеры наиболее употребимых схем логически правильных рассуждений (некоторые их них приведем без пояснений) (табл. 62): Таблица 62
Пример 52. Следующие рассуждения не являются правильными:
2.3.2. Метод Вонга Пусть дана клауза в своей наиболее общей форме: В1, В2, …, Вn Þ А1, А2, …,An Шаг 1. Снятие отрицаний с посылок и заключений. С этой целью нужно опустить знак отрицаний у Ai и Bj и перенести их в противоположные стороны относительно символа Þ. Шаг 2. Если слева от символа Þ встречается конъюнкция, а справа дизъюнкция, то их следует заменить на запятые. Шаг 3. Если после предыдущих шагов оказалось, что связкой, расположенной слева от Þ, является дизъюнкция, а справа – конъюнкция, то образуются две новые клаузы, каждая из которых содержит одну из двух подформул, заменяющих исходную клаузу. Шаг 4. Если одна и та же буква находится с обеих сторон символа Þ, то такая строка считается доказанной. Исходная клауза является теоремой, если все ветви оканчиваются истинными клаузами. В противном случае переходим к шагу 3. Пример 53. Выяснить, является ли клауза теоремой:
Решение. Шаг 1. Избавляемся от отрицаний. В результате получаем: Шаг 2. Поскольку слева от символа Þ не встречается конъюнкция, а справа не встречается дизъюнкция, то шаг 2 как таковой отсутствует.
Так как есть не доказанные строки, то исходная клауза теоремой не является. Пример 54. Выяснить, является ли клауза теоремой:
Решение. Представим ход доказательства в виде дерева (рис. 12). Поскольку все строки доказаны, то исходная клауза является теоремой.
2.3.3. Метод резолюций Методику продемонстрируем на примере. Пусть требуется доказать:
Сначала поступают точно так же, как и по методике Вонга, только необходимо преобразовать клаузу таким образом, чтобы слева от символа Þ был ноль Æ:
Затем из дизъюнктов составляют резолюции до тех пор, пока не получится ноль. Выпишем по порядку все посылки и далее начнем их «склеивать». Дизъюнкты можно перебирать автоматически в соответствии с возрастанием порядковых номеров. Такая стратегия поиска нуля очень непродуктивна. К решению данной задачи можно подойти творчески. В итоге получим:
Иначе, произведенные раннее преобразования, можно представить в следующем виде:
2.4. Логика предикатов 2.4.1. Основные понятия, связанные с предикатами В высказывании все четко: это конкретное утверждение о конкретных объектах – истинное или ложное. Предикат – предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить истинно оно или ложно. Логика предикатов представляет собой развитие логики высказываний. С помощью формул логики высказываний можно описать и исследовать структуру сложных высказываний, установить их истинность или ложность в зависимости от истинности или ложности входящих в нее простых высказываний. Для описания внутренней логической структуры простых высказываний используется понятие предиката. Определение. N-местным предикатом, определенном на множествах М1, М2, …, Мn, называется предложение, содержащее n переменных х1, х2, …, хn, превращающееся в высказывание при подстановке вместо этих переменных любых конкретных элементов из множеств М1, М2, …, Мn соответственно. Обозначение. Чаще всего предикаты обозначают большими латинскими буквами, а число переменных указывает на его размерность: P(x1, x2, …, xn). Предикат также называют функцией-высказыванием. Пример 55. Рассмотрим три высказывания: А – «Рубль – валюта России»; В – «Доллар – валюта России»; С – «Доллар – валюта США». Высказывания А и С – истинны, В – ложно. Если вместо конкретных наименований валюты в выражениях А, В подставить предметную переменную х и определить ее на множестве наименований денежных единиц М, то получим одноместный предикат P(x): «х – валюта России», где х Î М. Если же в высказывания подставить не только предметную переменную х, определенную на множестве М, но и вместо наименований стран ввести предметную переменную у, определенную на множестве названий стран У, то получим двуместный предикат: Q(x, у): «х - валюта страны у», где х Î М, у Î У. Чаще всего предикаты задают высказывательными формами, как показано выше. Однако предикат можно задать таблицей. Такой способ пригоден только для предикатов, область определения которых – конечное множество. Пример 56. Пусть задан одноместный предикат P(x), хÎМ, где М = {1, 2, 3, 4, 5}. Значение предиката можно задать таблицей (табл. 63): Таблица 63
Пример 57. Предикат задан высказывательной формой Р(х): «в слове х буква «а» встречается не более двух раз», хÎМ, где М = {конь, стол, карандаш, зал, чаша, барабан}. Построим таблицу значений для данного предиката (табл. 64): Таблица 64
Определение. Множеством истинности предиката Р(х1, х2, …, хn), заданного на множествах М1, М2, …, Мn, называется совокупность всех упорядоченных n-систем (а1, а2, …, аn), в которых Это множество будем обозначать Р+. Пример 58. Определить множество истинности предикатов, заданных на соответствующих множествах: 1. Р(х): «х кратно 3», хÎМ, где М = {1, 2, 3, 4, 5, 6, 7, 8, 9}; 2. G(x, y): «
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 703; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.178 (0.202 с.) |
 .
.



 тоже самодвойственна.
тоже самодвойственна. ;
;


 , причем на каждом наборе <i1, …, ik> все аij (j = 1, …, k) различны, aj Î {0, 1}.
, причем на каждом наборе <i1, …, ik> все аij (j = 1, …, k) различны, aj Î {0, 1}. Поскольку сокращенная ДНФ содержит отрицания, то функция не является монотонной.
Поскольку сокращенная ДНФ содержит отрицания, то функция не является монотонной. Поскольку сокращенная ДНФ не содержит отрицаний, то функция является монотонной.
Поскольку сокращенная ДНФ не содержит отрицаний, то функция является монотонной. , так как она содержит отрицания, то f Ï M.
, так как она содержит отрицания, то f Ï M. 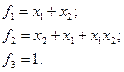

 от булевой функции f по переменной xi есть сумма по модулю 2 соответствующих остаточных функций:
от булевой функции f по переменной xi есть сумма по модулю 2 соответствующих остаточных функций: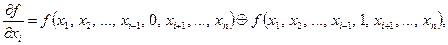
 от булевой функции называется число конституент этой производной.
от булевой функции называется число конституент этой производной.

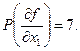










 получено при дифференцировании функции f по переменным х2 и х4, максимальное значение
получено при дифференцировании функции f по переменным х2 и х4, максимальное значение  получено при дифференцировании функции f по переменной х3.
получено при дифференцировании функции f по переменной х3.






 , то неверно А
, то неверно А



 следует
следует 







 .
.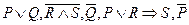 .
. .
.
 .
.
 .
.





 таких, что данный предикат обращается в истинное высказывание при подстановке х1=а1, х2=а2, …, хn=аn.
таких, что данный предикат обращается в истинное высказывание при подстановке х1=а1, х2=а2, …, хn=аn.


