
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равносильность формул логики предикатов
Пусть формулы А и В имеют одно и то же множество свободных переменных. Определение. Формулы А и В равносильны в данной интерпретации, если на любом наборе значений свободных переменных они принимают одинаковые значения (т. е. если формулы выражают в данной интерпретации один и тот же предикат). Определение. Формулы А и В равносильны на множестве М, если они равносильны во всех интерпретациях, заданных на множестве М.. Определение. Формулы А и В равносильны в логике предикатов, если они равносильны на всех множествах (АºВ). Укажем несколько правил перехода от одних формул к другим, им равносильным. Для формул логики предикатов сохраняются все равносильности и правила равносильных преобразований логики высказываний. Утверждение. Всякую формулу логики предикатов, содержащую символы ® и», можно преобразовать в равносильную ей формулу, не содержащую этих символов. Кроме этого, существуют следующие правила: 1. Перенос квантора через отрицание
2. Вынос квантора за скобки
3. Перестановка одноименных кванторов "х "у А(х, у) º "у "х А(х, у), $х $у А(х, у) º $у $х А(х, у). 4. Переименование связанных переменных. Заменяя связанную переменную формулы А другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора получаем формулу, равносильную А. Определение. Формула А, равносильная формуле В, и не содержащая символов ®,», а также составных формул под знаком отрицания, называется приведенной формой формулы В. Теорема. Для любой формулы существует равносильная ей приведенная формула, причем множества свободных и связанных переменных этих формул совпадают. Пример 66. Преобразовать в приведенную форму формулу Решение.
Определение. Приведенная формула называется нормальной (ПНФ), если она не содержит символов кванторов или все кванторы стоят в ее начале, а область действия каждого из них распространяется до конца формулы. Пример 67. Преобразовать в ПНФ формулы: 1. 2. Решение. 1.
2.
3. ТЕОРИЯ ГРАФОВ Графические представления в широком смысле – любые наглядные отображения исследуемой системы, процесса, явления на плоскости. К ним могут быть отнесены рисунки, чертежи, графики зависимостей характеристик, планы-карты местностей, блок-схемы процессов, диаграммы и т.п. Такие изображения наглядно представляют различные взаимосвязи и взаимообусловленности: топологические, хронологические, логические, структурные, причинно-следственные и др.
В последние несколько лет теория графов стала важнейшим математическим инструментом, широко используемым во многих областях науки, начиная с исследования операций и лингвистики и кончая химией и генетикой. В то же самое время она выросла в самостоятельную математическую дисциплину. Для ее понимания требуется только знание элементарной теории множеств и теории матриц.
3.1. Основные определения Определение. Пара (V(G), E(G)) называется простым графом, если V(G) – непустое конечное множество элементов, называемых вершинами (или узлами, или точками), а E(G) – конечное множество неупорядоченных пар различных элементов из V(G), называемых ребрами (или линиями). В простом графе данную пару вершин может соединять не более чем одно ребро. Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v1, v2, если оно соединяет эти вершины и наоборот, каждая из вершин v1, v2 инцидентна ребру е. Рассмотрим графическое представление графов (табл. 66). Таблица 66 Графическое представление графов
Многие результаты, полученные для простых графов, без труда модно перенести на более общие объекты, в которых две вершины могут быть соединены более чем одним ребром. Кроме того, часто бывает удобно снять ограничение, состоящее в том, что ребро должно соединять две различные вершины, и допустить существование петель. Получающийся при этом объект, в котором могут быть и кратные ребра и петли называется графом (псевдографом). Псевдограф без петель называется мультиграфом.
Определение. Если ребро задаётся упорядоченной парой вершин, то оно является ориентированным. Если каждое ребро графа ориентированное, то граф называется ориентированным или орграфом. Иногда удобно преобразовать неориентированный граф в ориентированный – заменой одного неориентированного ребра парой ребер с противоположной ориентацией. Приведем ряд понятий и определений для ориентированных и неориентированных графов. Там, где это специально не оговорено, те же понятия и определения переносятся без изменений на ориентированные и неориентированные псевдографы.
3.1.1. Смежность, инцидентность, степени Определение. Если е = {v, w} – ребро графа, то вершины v, w называются концами ребра е; в этом случае также говорят, что ребро е соединяет вершины v, w. Определение. Если е = {v, w} – дуга орграфа, то вершина v называется началом, а вершина w – концом дуги е; в этом случае также говорят, что дуга е исходит из вершины v и заходит в вершину w. Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v, w, если оно соединяет эти вершины и наоборот, каждая из вершин v, w инцидентна ребру е. Определение. Две вершины называются смежными, если существует ребро, концами которого они являются. Два ребра называются смежными, если они имеют общую вершину. Определение. Степенью вершины v графа G называется число d(v) ребер графа, которым инцидентна эта вершина. Определение. Вершина, локальная степень которой равна 0, называется изолированной; степень которой равна 1 – висячей. Замечание. В случае неориентированного псевдографа обычно считается, что вклад каждой петли, инцидентной некоторой вершине v, равен 2 (тогда как вклад любого другого ребра, инцидентного вершине v, равен 1). Определение. Полустепенью исхода (захода) вершины v орграфа D называется число d+(v) (d -(v)) дуг орграфа D, исходящих из вершины v (заходящих в вершину v). Замечание. В случае ориентированного псевдографа вклад каждой петли, инцидентной некоторой вершине v, равен 1, как в d+(v), так и в d -(v). Количество вершин и ребер в графе G обозначим соответственно через n(G) и m(G), а количество вершин и дуг в орграфе D – через n(D) и m(D). Утверждение. Для любого псевдографа G выполняется равенство Утверждение. Для любого ориентированного псевдографа D выполняется равенство Пример 69. Найти локальные степени графа (рис. 19) и орграфа (рис. 20). Решение.
d (u) = 2; d (v) = 2; d (z) = 3; d (m) = 1. 3.1.2. Изоморфизм, гомеоморфизм Определение. Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2. Из определения следует, что изоморфные графы можно одинаково изображать графически и отличаться они будут только метками вершин. Изоморфизм графов есть отношение эквивалентности. Пример 70. На рисунке 21 изображены три изоморфных графа. На рисунке 22 изображены два неизоморфных графа.
Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма.
Пример 71. С точностью до изоморфизма существует ровно четыре простых графа с тремя вершинами и одиннадцать с четырьмя вершинами. Постройте эти графы. Решение. 1. Построим четыре простых графа с тремя вершинами с точностью до изоморфизма (рис. 23):
2. Построим одиннадцать простых графов с четырьмя вершинами с точностью до изоморфизма (рис. 24):
Определение. Орграф D1 называется подразбиением орграфа D2, если орграф D1 можно получить из D2 путем последовательного применения операции подразбиения дуг. Аналогично определяется подразбиение графа. Определение. Орграфы D1, D2 называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными. 3.1.3. Матричное задание графов. Матрицы смежности, инцидентности Пусть D = (V, Х) – орграф, где V={v1, v2, …,vn}, X={x1, x2, …, xm}. Определение. Матрицей смежности орграфа D называется квадратная матрица A(D)=[aij] порядка n, у которой
Определение. Матрицей инцидентности орграфа D называется (n´m) –матрица B(D)=[bij], у которой
Введем также матрицы смежности и инцидентности для неориентированных графов. Пусть G = (V, X) – граф, где V={v1, v2, …,vn}, X={x1, x2, …, xm}. Определение. Матрицей смежности графа G называется квадратная матрица A(G)=[aij] порядка n, у которой
Определение. Матрицей инцидентности графа G называется (n´m) –матрица B(G)=[bij], у которой
С помощью введенных матриц удобно задавать графы для обработки на ЭВМ. Используя матрицу смежности легко определить локальные степени вершин графа: сумма элементов матрицы по строке равна локальной степени соответствующей вершины. Для орграфов по строке определяются полустепени исхода, по столбцам – полустепени захода. Пример 72. Построить матрицы смежности и инцидентности для графа G = (V, X) (рис. 25). Решение.
Поскольку граф не имеет петель, то на главной диагонали стоят все нули. Для любого графа матрица смежности симметрична относительно главной диагонали.
Напомним, что в строках указываются вершины, в столбцах – ребра. Матрица инцидентности может быть как квадратной, так и прямоугольной.
Пример 73. Построить матрицы смежности и инцидентности для орграфа D= (V, X) (рис. 27). Решение.
Матрица инцидентности имеет вид
3.1.4. Примеры графов. Операции над графами
Определение. Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают Nn. Заметим, что у вполне несвязного графа все вершины изолированы. Определение. Простой граф, в котором любые две вершины смежны, называется полным. Полный граф обозначают Кn.
Заметим, что для полного графа выполняется равенство Определение. Граф, у которого все вершины имеют одну и ту же локальную степень n, называется регулярным (или однородным) степени n. Регулярные графы степени 3 называются кубическими (или трехвалентными). Пример 75.
Среди регулярных графов особенно интересны так называемые платоновы графы – графы, образованные вершинами и ребрами пяти правильных многогранников – Платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра. Пример 76.
Определение. Допустим, что множество вершин графа G можно разбить на два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-нибудь вершиной из V2, тогда данный граф называется двудольным. Двудольный граф можно определить и по-другому – в терминах раскраски его вершин двумя цветами, скажем красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы каждое ребро имело один конец красный, а другой – синий. Определение. Если в двудольном графе каждая вершина из V1 соединена с каждой вершиной из V2, то граф называется полным двудольным. Обозначение. Кm. n Заметим, что граф Кm. n имеет ровно m + n вершин и mn ребер. Пример 77.
На рис. 31 изображены двудольные графы. Определение. Объединением графов Определение. Пересечением графов Определение. Соединением графов G1 и G2 является новый граф, у которого V=V1ÈV2, а множеством ребер являются все ребра первого и второго графа и ребра, соединяющие между собой каждую вершину первого графа с первой вершиной второго графа. Определение. Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае. Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой связности графа. Определение. Связный регулярный граф степени 2 называется циклическим графом. Обозначается Сn (рис. 32). Определение. Соединение графов N1 и Cn-1 (n³3) называется колесом с n вершинами. Обозначается Wn (рис. 32).
Пример 78.
Определение. Дополнением простого графа G называется простой граф с множеством вершин V(G), в котором две вершины смежны тогда и только тогда, когда они не смежны в исходном графе. Обозначение. Другими словами, дополнением графа является граф, содержащий все вершины исходного графа и только те ребра, которых не хватает исходному графу для того, чтобы он стал полным. Определение. Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа.
3.1.5. Маршруты, цепи, циклы Введем понятие маршрута для графа G = (V, E) (и соответственно понятие пути для орграфа D = (V, E)). Определение. Маршрутом в данном графе G называется конечная последовательность ребер вида {v0, v1}, {v1, v2}, …, {vm-1, vm} (обозначаемая также v0®v1®v2®…®vm). Каждому маршруту соответствует последовательность вершин v0v1v2…vm; v0 – начальная вершина, а vm – конечная вершина маршрута.Одна и та же вершина может одновременно оказаться начальной, конечной и внутренней. Таким образом, мы будем говорить о маршруте из v0 в vm. Определение. Длиной маршрута называется число ребер в нем. Определение. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все вершины тоже различны (кроме, может быть, начальной и конечной вершин). Определение. Цепь или простая цепь замкнуты, если начальная и конечная вершины совпадают. Определение. Замкнутая простая цепь, содержащая, по крайней мере, одно ребро, называется циклом. Определение. Обхватом графа называется длина его кратчайшего цикла. 3.1.6. Связность. Компоненты связности Определение. Вершина w орграфа D (графа G) достижима из вершины v, если либо v=w, либо существует путь из v в w(маршрут, соединяющий v, w). Дадим более удобное определение связных графов. Определение. Граф называется связным, если для любых двух его вершин v, w существует простая цепь из v в w. Определение. Граф (орграф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v, w (из v и w). Определение. Орграф называется односторонне связным, если для любых его двух вершин, по крайней мере, одна достижима из другой. Определение. Если граф не является связным, то он называется несвязным. Определение. Компонентой связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа. В дальнейшем количество компонент связности графа будем обозначать k.
Данный граф не является связным: k = 3.
Данный граф является связным: k = 0.
Теорема. Пусть G – простой граф с n вершинами и k компонентами. Тогда число m его ребер удовлетворяет неравенствам
Следствие. Любой простой граф с n вершинами и более чем (т-1)(т-2)/2 ребрами связен.
При исследовании графов возникает вопрос: насколько сильно связен связный граф? Этот вопрос можно сформулировать и так: сколько ребер нужно удалить из графа, чтобы он перестал быть связным? Под операцией удаления вершин из графа будем понимать операцию, заключающуюся в удалении некоторой вершины вместе с инцидентными ей ребрами. Определение. Вершина графа, удаление которой увеличивает число компонент связности, называется разделяющейся. Определение. Разделяющим множеством связного графа G называется такое множество его ребер, удаление которого приводит к несвязному графу. Определение. Разрезом называется такое разделяющее множество, никакое собственное подмножество которого не является разделяющим. Определение. Разрез, состоящий из одного ребра, называется мостом (перешейком). Пример 80.
Разрезом является множество ребер {e1, e2}. В графе возможно выделить несколько разделяющих множеств и разрезов.
3.2. Задачи поиска маршрутов (путей) в графе (орграфе) 3.2.1. Поиск путей (маршрутов) с минимальным числом дуг (ребер) При решении некоторых прикладных задач нередко возникает необходимость найти маршрут, соединяющий заданные вершины в графе G. Данная задача решается при использовании алгоритма Тэрри. Рассмотрим более сложную задачу: нахождение пути (маршрута) с минимальным числом дуг (ребер). Определение.Путь в орграфе D из вершины v в вершину w, где v ¹ w, называется кратчайшим, если он имеет минимальную длину среди всех путей орграфа D из v и w. Аналогично определяется и кратчайший маршрут в графе G. Утверждение. Любой кратчайший путь (маршрут) является простой цепью. Рассмотрим задачу поиска минимального пути (маршрута). Введем некоторые обозначения. Пусть D=(V, X) – орграф, vÎV, V1ÌV. Обозначим D(v)={wÎV| (v, w)ÎX} – образ вершины v; D-1(v)={wÎV| (w,v)ÎX} – прообраз вершины v; Пусть D=(V, X) – орграф с n ³ 2 вершинами и v, w – заданные вершины из V, где v ¹ w. Опишем алгоритм поиска кратчайшего пути из v в w в орграфе D. Алгоритм фронта волны. Шаг 1. Помечаем вершину v индексом 0. Затем помечаем вершины, принадлежащие образу вершины v, индексом 1. Множество вершин с индексом 1 обозначаем FW1(v). Полагаем k=1. Шаг 2. Если FWk(v)=Æ или выполняется k=n-1, wÏFWk(v), то вершина w не достижима из v, и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3. Шаг 3. Если wÏFWk(v), то переходим к шагу 4. В противном случае существует путь из v в w длины k, и этот путь является кратчайшим. Последовательность вершин vw1w2…wk-1w, где
и есть искомый кратчайший путь из v и w. На этом работа алгоритма заканчивается. Шаг 4. Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом k. Множество вершин с индексом k+1 обозначаем FWk+1(v). Присваиваем k:=k+1 и переходим к шагу 2. Замечание. Множество FWk(v) обычно называют фронтом волны k -го уровня. Замечание. Вершины w1w2…wk-1, вообще говоря, могут быть выделены неоднозначно. Эта неоднозначность соответствует случаям, когда существует несколько различных кратчайших путей из v и w. Пример 81. Определить кратчайший путь из v1 и v6 в орграфе D, заданном матрицей смежности (табл. 67). Таблица 67
Решение. Согласно алгоритму Фронта волны, последовательно определяем FW1(v1) = {v4, v5}; FW2(v1) = D(FW1(v1))\{v1, v4, v5} = {v2, v3}; FW3(v1) = D(FW2(v1))\{v1, v2, v3, v4, v5} = {v6}. Таким образом, v6 Î FW3(v1), а значит, существует путь из v1 в v6 длины 3, и этот путь является кратчайшим. Найдем теперь кратчайший путь из v1 в v6. Определим множество
Выберем любую вершину из найденного множества, например вершину v3. Определим далее множество
Выберем любую вершину из найденного множества, например вершину v5. Тогда v1v5v3v6 – искомый кратчайший путь из v1 в v6 (длины 3) в орграфе D.
3.2.2. Расстояния в графе. Диаметр, центр, радиус графа Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w). Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами. Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Для графа G, изображенного на рисунке 34, найти радиус, диаметр и центры. Решение. Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали. С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения:
3.2.3. Нахождение минимального пути в нагруженном графе Определение. Назовём орграф Тем самым и нагруженном орграфе Для любого пути Определение. Путь в нагруженном орграфе Рассмотрим теперь задачу поиска минимальных путей (маршрутов) в нагруженном орграфе (графе). При этом для определенности рассуждения будем проводить для орграфа (для графа они аналогичны). Пусть
Введем также в рассмотрение квадратную матрицу
которую будем называть матрицей длин дуг нагруженного орграфа Следующее утверждение дает простые формулы для вычисления величин Утверждение.
Используя данное утверждение, нетрудно описать алгоритм нахождения таблицы значений величин Алгоритм Форда – Беллмана нахождения минимального пути в нагруженном орграфе Шаг 1. Пусть мы уже составили таблицу величин Шаг 2. Пусть Шаг 3. Последовательно определяем номера
...... (4)
Из (4) с учётом того, что
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.123 (0.183 с.) |



 .
.
 ;
; .
.

 - точка в пространстве
- точка в пространстве
 - направленный отрезок, ориентированное
ребро
- направленный отрезок, ориентированное
ребро
 - отрезок, неориентированное ребро
- отрезок, неориентированное ребро
 - замкнутый отрезок, петля
- замкнутый отрезок, петля
 Пример 68.
Пример 68.









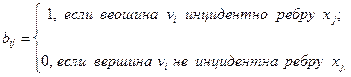
 Матрица смежности имеет вид
Матрица смежности имеет вид .
. Для того, чтобы построить матрицу инцидентности необходимо пронумеровать ребра графа (рис. 26). Матрица инцидентности имеет вид:
Для того, чтобы построить матрицу инцидентности необходимо пронумеровать ребра графа (рис. 26). Матрица инцидентности имеет вид:
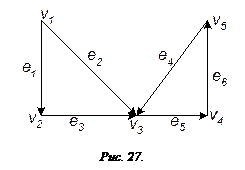 Матрица смежности имеет вид:
Матрица смежности имеет вид:

 Рассмотрим некоторые важные типы графов.
Рассмотрим некоторые важные типы графов. Пример 74.
Пример 74.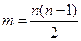 , где m – число ребер, n – число вершин графа.
, где m – число ребер, n – число вершин графа. Известным примером кубического графа является граф Петерсона (рис. 29).
Известным примером кубического графа является граф Петерсона (рис. 29). На рис. 30 приведен граф, соответствующий кубу.
На рис. 30 приведен граф, соответствующий кубу.
 называется граф
называется граф 
 , называется граф
, называется граф 


 Пример 79.
Пример 79.

 Для графа, изображенного на рис.33, каждое из множеств {e1, e2, e5} и {e3, e6, e7, e8} является разделяющим.
Для графа, изображенного на рис.33, каждое из множеств {e1, e2, e5} и {e3, e6, e7, e8} является разделяющим. - образ множества вершин V1;
- образ множества вершин V1;  - прообраз множества вершин V1. Пусть G=(V, X) – граф, vÎV, V1ÌV. Обозначим G(v)={wÎV|{v, w}ÎX} – образ вершины v;
- прообраз множества вершин V1. Пусть G=(V, X) – граф, vÎV, V1ÌV. Обозначим G(v)={wÎV|{v, w}ÎX} – образ вершины v;  - образ множества вершин V1.
- образ множества вершин V1.


 Пример 82.
Пример 82.
 для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4. нагруженным, если на множестве дуг
нагруженным, если на множестве дуг  определена некоторая функция
определена некоторая функция  , которую часто называют весовой функцией.
, которую часто называют весовой функцией. каждой дуге
каждой дуге  поставлено в соответствие некоторое действительное число
поставлено в соответствие некоторое действительное число  . Значение
. Значение  .
. нагруженного орграфа
нагруженного орграфа  сумму длин входящих в
сумму длин входящих в  в вершину
в вершину  , где
, где  , называется минимальным, если он имеет минимальную длину среди всех путей орграфа
, называется минимальным, если он имеет минимальную длину среди всех путей орграфа  .
. ,
,  . Введем величины
. Введем величины  , где
, где  ,...,
,...,  ,
,  ,
,  ,... Для каждых фиксированных
,... Для каждых фиксированных  и
и  величина
величина  в
в  , содержащих не более
, содержащих не более  . Кроме того, если произвольную вершину
. Кроме того, если произвольную вершину 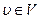 считать путем из
считать путем из  , при этом
, при этом (1)
(1) порядка
порядка 



 .
. - номер столбца). Действительно, используя рекуррентные соотношения (2), (3) и исходя из (1), последовательно определяем набор величин
- номер столбца). Действительно, используя рекуррентные соотношения (2), (3) и исходя из (1), последовательно определяем набор величин  ((
(( , а затем шаг за шагом увеличиваем значение
, а затем шаг за шагом увеличиваем значение 

 . Если
. Если  не достижима из
не достижима из  конечны). В этом случае работа алгоритма заканчивается.
конечны). В этом случае работа алгоритма заканчивается. . Тогда число
. Тогда число  выражает длинны любого минимального пути из
выражает длинны любого минимального пути из  , при котором выполняется равенство
, при котором выполняется равенство  . По определению чисел
. По определению чисел  получим, что
получим, что  - минимальное число дуг в пути среди всех минимальных путей из
- минимальное число дуг в пути среди всех минимальных путей из  такие что
такие что


 , имеем
, имеем  , откуда, используя (1), получаем
, откуда, используя (1), получаем (5)
(5)


