Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойств выборочных вариаций (дисперсий) и ковариаций.
Для дальнейшего изложения нам понадобится установить ряд правил, которые можно использовать при преобразовании выражений, содержащих выборочные вариации и ковариации. Пусть а — некоторая постоянная, а х, у, z — переменные, принимающие в i-м наблюдении значения xi,yi,zi,i=1,..., п (n — количество наблюдений). Тогда а можно рассматривать как переменную, значение которой в i-м наблюдении равно а, и
откуда следует свойство: 1. Cov(x, a) = 0. Далее, нетрудно видеть, что имеют место равенства: 2. Cov(x, у) = Cov(y, х); 3. Cov(x. x) = Var(x). Кроме того,
откуда следует свойство:
4. Cov(ax. у) = aCov(x, у).
5. Cov(x. у + z) =Cov(x, у) + Cov(x,z). На основе вышеназванных свойств находим, что 6. Var(a)=0, т. е. постоянная не обладает изменчивостью и 7. Var(ax)=a2Var(x). Таким образом, при изменении единицы измерения переменной в раз, во столько же раз преобразуется и величина стандартного отклонения этой переменной (напомним, что стандартное отклонение равно квадратному корню из дисперсии). 8. Var(x+a)=Var(x) т. е. сдвиг начала отсчета не влияет на вариацию переменной. Далее, имеем: Var(x+y)=Cov(x+y,x+y)= Cov(x, х) + Cov(x, у) + Cov(y, x) + Cov(x, у). Таким образом, доказано свойство 9.Var(x+y)=Var(x)+Var(y)+2Cov(x,y), означающее, что вариация суммы двух переменных отличается от суммы вариаций этих переменных на величину, которая равна удвоенному значению ковариации между названными переменными.
Свойства остатков Теперь установим почти очевидные соотношения, которые следуют из условии минимума критерия наименьших квадратов. Определим величину ŷi=a +bx,
— оценку переменной у при оптимальных значениях коэффициентов регрессии и фиксированном значении х в i-ом наблюдении. Такую оценку называют прогнозом зависимой переменной. Тогда, очевидно, ошибка модели в i-ом наблюдении будет равна e i=yi- ŷi и из условия следует, что
т. е сумма квадратов ошибок оценок переменной у (остатков модели) при оптимальных параметрах регрессии а и b равна нулю. Далее, вытекает, что т. е., при оптимальных параметрах регрессии ошибки ортогональны наблюдениям независимой переменной.
Несмещенность МНК-оценок Статистическая оценка некоторого параметра называется несмещенной, если ее математическое ожидание равно истинному значению этого параметра.
Для случая парной линейной регрессии это означает, что опенки а и b будут несмещенными, если М{а} = α, M{b}=β.
Применив формулу для коэффициента,а также полученное выше соотношение, составим выражение:
Далее, поскольку х — неслучайная величина, будем иметь:
и, таким образом, оценка b является несмещенной. Несмещенность оценки а следует из цепочки равенств:
Замечание. Свойство несмещенности оценок можно доказать и при более слабой форме 4-го условия Гаусса-Маркова, когда х—случайная, но некоррелированная со случайной переменной u, величина.
Состоятельность оценок Свойство состоятельности оценок заключается в том, что при неограниченном возрастании объема выборки, значение оценки должно стремиться (по вероятности) к истинному значению параметра, а дисперсии оценок должны уменьшаться и в пределе стремиться к нулю. Дисперсии оценок коэффициентов регрессии определяются выражениями:
Или. используя равенство
Вывод: чем больше число наблюдений n, тем меньше будут дисперсии ошибок.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.62.45 (0.005 с.) |
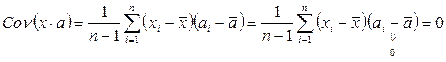
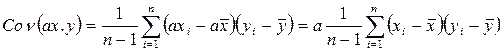 ,
, ;
; 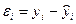




 ;
; 
 , можно записать в виде:
, можно записать в виде: