
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанное соединение элементов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
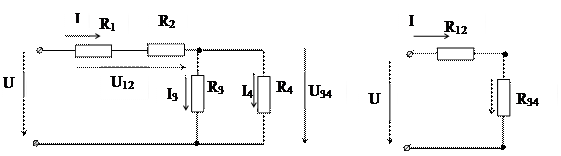
Смешанным соединением элементов называют все возможные сочетания последовательного и параллельного соединений. В такой цепи может быть различное число узлов и ветвей. Один из примеров смешанного соединения представлен на схеме (рис. 1.3, а).
а) б)
в) Рис.1.3 Схема смешанного соединения элементов (а) и ее эквивалентные схемы (б, в)
Для расчета такой схемы необходимо сначала определить эквивалентные сопротивления тех частей схемы, которые представляют собой только последовательное или только параллельное соединение. В предложенной схеме элементы R1 и R2 соединены между собой последовательно, а элементы R3 и R4 – параллельно. Используя приведенные ранее соотношения (1.7) и (1.13), можно заменить R1 и R2 эквивалентным сопротивлением R12, а элементы R3 и R4 –эквивалентным сопротивлением R34:
R12 = R1+R2 (1.18)
R34 = В результате такой эквивалентной замены получится схема, изображенная рис.1.3 (б), в которой элементы R12 и R34 соединены между собой последовательно. Для этой схемы эквивалентное сопротивление
Rэкв=R12 + R34 (1.20)
В результате такой эквивалентной замены получим схему, изображенную на рис.1.3 (в). Определим ток, протекающий в этой цепи:
Это ток источника питания и ток в элементах R1 иR2 реальной цепи. Найдем напряжения на участке цепи с сопротивлением R12 и на участке цепи с сопротивлением R34: U12 = I · R 12; U34 = I · R 34 (1.22)
Токи I3 и I4 можно найти по закону Ома:
Для проверки правильности расчета схемы смешанного соединения элементов можно воспользоваться 1-м и 2-м законами Кирхгофа, а также законом баланса мощности. Должны выполняться соотношения: I = I3 + I4;
Uист = U12 + U34;
Рист=ΣРпр= Р1 + Р2 + Р3 + Р4 Здесь Р1 =
Подобным образом можно рассчитать и другие, более сложные схемы электрических цепей со смешанным соединением элементов. Существуют и другие схемы эквивалентных преобразований, так как не все схемы сводятся к комбинации последовательно и параллельно соединенных элементов. Такие схемы будут рассмотрены в следующем подразделе.
ЛЕКЦИЯ 2.
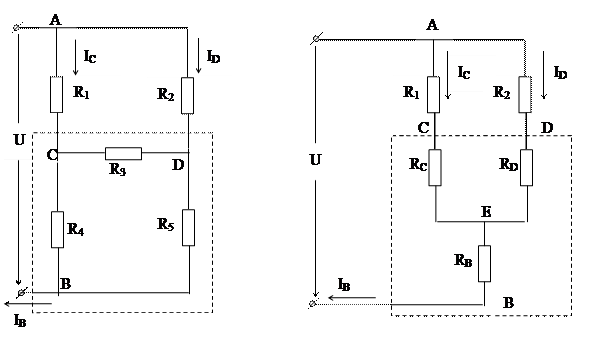
1.3.4 Преобразование «треугольник» - «звезда». На рис. 1.5 показана одна из разновидностей мостовых схем, называемая четырехплечий мост или мост Уитстона. Ни одну пару сопротивлений в этой схеме нельзя квалифицировать как последовательно или параллельно включенные. Следовательно, к ней неприменимы основные правила нахождения эквивалентных сопротивлений. Расчет эквивалентного сопротивления схем такого типа осуществляется методом эквивалентных преобразований.
При эквивалентном преобразовании часть цепи заменяется новыми элементами с другим их соединением. При этом сопротивления новых элементов должны быть такими, чтобы проведенная замена не привела к изменению распределения токов и напряжений в участках цепи, не подвергшихся изменениям. В этом случае новую цепь можно считать эквивалентной старой. Рассмотрим одно из широко распространенных эквивалентных преобразований - преобразование "треугольник - звезда". Участок цепи "трехлучевая звезда" и подключенными к тем же точкам исходной цепи В, С, D (рис. 1.4, справа); при этом в новой схеме, называемой схемой замещения, добавляется еще один узел - Е.
Рис. 1.4 Применим это преобразование для расчета эквивалентного сопротивления четырехплечего моста. Заменим резисторы R3, R4и R5, включенные "треугольником" между узлами В, С и D (выделенная область на рис. 1.5), новыми резисторами RB,RC,RD, соединенными в трехлучевую звезду (выделенная область на рис. 1.6. В результате замены элементов ток, вытекающий из узла В, и токи, втекающие в узлы С и D (токи IB, ICи IDсоответственно), не должны измениться. Это значит, что не должна измениться проводимость схемы между узлами В-С, B-D и C-D.
Рис. 1.5 Рис.1.6
Рассмотрим проводимость обеих схем между узлами В-С. В исходной схеме эта проводимость осуществляется по двум каналам протекания тока: через резистор RA (его проводимость равна Суммарная проводимость обоих каналов составляет Аналогично рассматриваются проводимости в обеих схемах между узлами B-D и C-D. В итоге получаем систему из трех линейных уравнений с тремя неизвестными, которую можно разрешить относительно RB, RC, RD, т.е. выразить последние через R3, R4,R5:
Рассчитанная таким образом схема замещения по своим свойствам эквивалентна исходной схеме. Расчет эквивалентного сопротивления схемы замещения не представляет труда. Заменим последовательную цепочку R1RC на один резистор R1C, сопротивление которого равно сопротивлению этой цепочки, т.е.R1+Rc. Аналогично заменим цепочку R2RD один резистор R2D, сопротивление которого равно R2+RD. В схеме теперь можно выделить два параллельных элемента: R1Cи R2RD. Заменим этот фрагмент схемы одним резистором R 1C2D . Эквивалентное сопротивление находится из уравнения
т.е. Теперь наша схема свелась к последовательному соединению элементов RB и R1C2D. Окончательно получаем
2. ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА.
Предварительные сведения. Параметры переменного тока. В электрических цепях, электро-, радио- и других установках широко применяются периодически изменяющиеся электродвижущие силы (э.д.с.), напряжения и токи. В электротехнике переменным током принято называть ток, изменяющий по закону:
i = Imaxsin(ωt + φ0i) (2.1)
Аналогично, переменным напряжением называют напряжение, изменяющееся по закону:
u = Umaxsin(ωt + φ0u) (2.2)
Здесь Imax и Umax – максимальные (или амплитудные) значения тока и напряжения соответственно, i и u – их мгновенные значения, φ0u, φ0i – начальная фаза колебания напряжения и тока,
f - частота переменного тока, равная числу полных колебаний в 1с. f = Здесь Т – период колебания. В европейских странах в качестве стандарта частоты принята частота f = 50 Гц, в США и Японии стандарт частоты f = 60 Гц. Такие частоты обеспечивают получение оптимальных частот вращения электродвигателей переменного тока и отсутствие заметного для глаза мигания осветительных ламп накаливания. Следует отметить, что иногда бывает оправданным применение электротехнических устройств повышенной или пониженной частоты. Графики переменного тока и переменного напряжения изображены на рис. 2.1.
Рис.2.1 Синусоидальный ток, так же как и постоянный, используется для совершения какой-либо работы, при этом электрическая энергия преобразуется в другие виды энергии (механическую, тепловую, и т.д.). Для того чтобы количественно оценить синусоидальный ток, используют значение постоянного тока, эквивалентного синусоидальному по совершаемой работе. Таким образом, вводится понятие действующего значения переменного тока. Действующим значением переменного синусоидального тока называется значение такого постоянного тока, при прохождении которого в одном и том же резисторе сопротивлением R за время одного периода Т выделяется столько же теплоты, сколько и при прохождении синусоидального тока. При синусоидальном токе i = Imaxsinωt количество теплоты, выделяемое в резисторе R за время Т, согласно закону Джоуля-Ленца Q~ = При постоянном токе количество теплоты, выделяемое за время Т Q = I2RT (2.5)
Согласно определению, Q~ = Q, тогда
Вычислим интеграл:
Подставив (2.7) в (2.6), получим: или: действующее значение синусоидального переменного тока
Аналогично, действующее значение синусоидального напряжения
Таким образом, действующие значения синусоидальных величин в Электроизмерительные приборы всегда показывают действующие значения тока и напряжения. Зная их, всегда можно вычислить амплитудные значения. Так, например, если вольтметр показывает 220В синусоидального напряжения, то амплитуда такого напряжения равна
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 3188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.186 (0.008 с.) |


 (1.19)
(1.19)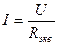 (1.21)
(1.21)
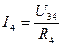 (1.23)
(1.23) · R1 ; Р2 =
· R1 ; Р2 =  · R2 ; Р3 =
· R2 ; Р3 = 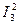 · R3 ; Р4 =
· R3 ; Р4 = 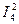 · R4.
· R4. 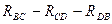 .,ограниченный узлами В, С, D (рис. 1.4, слева), заменяется новыми элементами
.,ограниченный узлами В, С, D (рис. 1.4, слева), заменяется новыми элементами 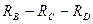 соединенными по схеме
соединенными по схеме
 ) и через цепочку резисторов
) и через цепочку резисторов 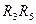 (её проводимость равна
(её проводимость равна  ).
).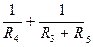 . В схеме замещения проводимость между этими же узлами осуществляется по цепочке резисторов RB RC и равна
. В схеме замещения проводимость между этими же узлами осуществляется по цепочке резисторов RB RC и равна  . Проводимости в обеих схемах должны быть равными.
. Проводимости в обеих схемах должны быть равными.
 =>
=> 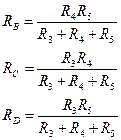 (1.24)
(1.24)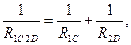 (1.25)
(1.25)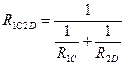 . (1.26)
. (1.26)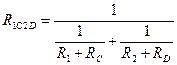 (1.27)
(1.27) - циклическая частота,
- циклическая частота,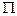 f,
f,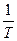 (2.3)
(2.3)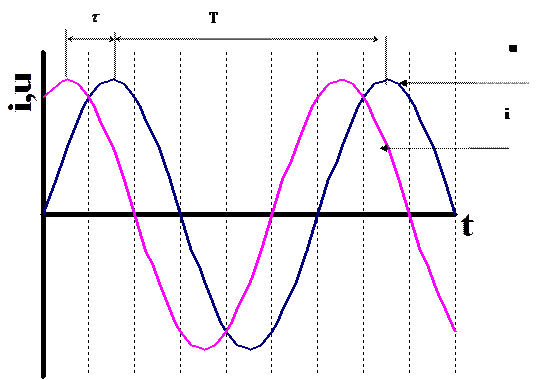
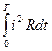 , (2.4)
, (2.4)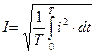 (2.6)
(2.6)
 (2.7)
(2.7)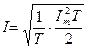 =
=  ,
,
 (2.9)
(2.9) раз меньше их амплитудных значений.
раз меньше их амплитудных значений.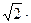 220 = 311 В.
220 = 311 В.


