
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для забезпечення конфіденційності »Содержание книги
Поиск на нашем сайте Для забезпечення конфіденційності» Навчальні питання Основні властивості еліптичних кривих Основні методи побудування загальних параметрів еліптичних кривих Аналіз основних проблемних питань відносно побудування загально системних параметрів для еліптичних кривих Крипто перетворення в гіпереліптичних кривих Додаток А ТаблицяА.1 – Параметри кривих над полем Завдання для самостійної роботи: - доопрацювати лекцію; - повторити матеріал що стосується афінного та проективного базисів. - довести що шифрування в в групі точок еліптичної кривої є оборотним.
Джерела, що рекомендуються до самостійної роботи 1. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Монографія. Харків, ХНУРЕ, Форт, 2012 р., 878 с. 2. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний конспект лекцій. Харків, ХНУРЕ, 2012 р. 3. Горбенко І. Д. Гриненко Т. О. Захист інформації в інформаційно-телекомунікаційних системах: Навч. посібник. Ч.1. Криптографічний захист інформації - Харків: ХНУРЕ, 2004 - 368 с. 4. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний носій до підручника. Харків, ХНУРЕ, 2012 р. Додаткова література 1.В. Задірака. Компьютерная криптологія. Підручник. К, 2002,504с. 2. А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с 3. Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с
Основні властивості еліптичних кривих Порядок еліптичної кривої Еліптична крива E над полем F(q) має бінарну операцію «+» складання точок E × E → E, для якої двом точкам Q1, Q2 на E може бути обчислена третя точка Q1 + Q2 на E. Еліптична крива E є абелевою групою щодо операції «+». Число точок еліптичної кривої E (включаючи точку нескінченності 0E) називається порядком E і позначається як #E(F(q)). Порядок кривої #E(F(q)) визначається згідно з теоремою Хасе [ ]: q + 1 – 2√q ≤ #E (F(q)) ≤ q + 1 + 2√q. (1.28) Ціле число t, визначене як t = q +1 – #E(F(q)), називається слідом. Теорема Хасе визначає межу по сліду. Аномальні та супер сингулярні криві Еліптична крива E, що визначена над полем F(q) з порядком #E(F(q))= pm, де q = pm, називається аномальною. Еліптична крива E, визначена над F(q) зі слідом t, кратним p, називається супер сингулярною. Аномальні криві вразливі до атак з використанням алгоритмів Аракі-Сатока, Смарта і Сімаіва [49]. Відносно супер сингулярних кривих існують вразливості, засновані на алгоритмах Фрея-Рюка та Менезіса-Окамото-Ванстона [47 - 49]. Параметри області еліптичної кривої Параметри області еліптичної кривої над F(q) Параметри еліптичної кривої над F(q), включаючи особливі випадки F(p) і F(2m), повинні визначати: – розмір поля q = pm, який визначає базове скінченне поле F(q), де p повинно бути простим числом, і вказує на базис, що використовується для представлення елементів поля у випадку m > 1; – якщо q = pm, причому p > 3, два елементи поля a і b у F(q), які визначають рівняння еліптичної кривої E: y2 = x3+ ax+ b; ⎯ якщо q = 2m, то два елементи поля a і b у F(2m), які визначають рівняння еліптичної кривої E: y2 + xy = x3 + ax2 + b; ⎯ якщо q = 3m, то два елементи поля a і b у F(3m), які визначають рівняння еліптичної кривої E: y2 = x3 + ax2 + b; ⎯ елементи поля xG і yG у F(q), які визначають базову точку G = (xG, yG) порядку n на еліптичній кривій E; ⎯ порядок n базової точки G; ⎯ значення кофактора h = #E(F(q))/n, якщо воно вимагається базовою схемою криптографічного перетворення. Генерація ключів еліптичної кривої Для заданого дійсного набору параметрів еліптичної кривої особистий ключ і відповідний відкритий ключ можуть бути генеровані таким чином: Вибирається випадкове або псевдовипадкове ціле d на відрізку [2, n–2], яке має бути захищене від несанкціонованого розкриття й бути непередбачуваним. Обчислюється точка P = (xP, yP) = dG. (1.31) Як ключова пара вибирається (P, d), де P – відкритий ключ, і d – особистий ключ. У деяких застосуваннях відкритий ключ обчислюється як e G, за умови, що de = 1 mod n. Недоліком метода P. Скуфа є велика степінь поліномів ділення, на основі яких виконано обчислення значення сліду відображення ендоморфізма Фробеніуса. Один зі шляхів подолання даного недоліку полягає в використанні поліномів меншого ступеня або розкладення поліномів ділення на множники, що дозволяє визначити координати точок крутіння використовуючи менший об’єм пам’яті в порівнянні з методом Р. Скуфа. В зв’язку з вказаним недоліком, метод P. Скуфа є методом, для програмної реалізації якого необхідно використовувати великі об’єми оперативної пам’яті, незважаючи на його поліноміальну складність. Тому цей метод недоцільно використовувати для полів з великою характеристикою. На основі метода, запропонованого Р. Скуфом, було розроблено вдосконалений метод обчислення порядку кривої під назвою SEA [4,5], який може бути застосовано, як над полем характеристики Можна зробити висновок, що вдосконалення Аткіна та Ілкіса, на основі яких побудований метод під назвою SEA, дозволяють зменшити обчислювальну складність методу Р. Скуфа шляхом використання поліномів степеня Обчислювальна складність алгоритму, який базується на методі SEA, та має таку ж назву дорівнює Застосування алгоритму Скуфа для обчислення порядку еліптичної кривої в стандарті ISO/IEC 15946-5 замість інших швидкодійних, в порівнянні з ним, алгоритмів пояснено тим, що цей алгоритм застосовано при розробці алгоритму перевірки числа на простоту Голдвассером і Килиана [8,9]. Алгоритм перевірки числа на простоту за допомогою еліптичних кривих Голдвассера і Килиана також включено до стандарту ISO/IEC 15946-5. Вказаний ймовірнісний алгоритм випадковим чином обирає еліптичну криву і перевіряє виконання деяких умов. На виході видається відповідь є число простим або складним, або знову здійснюється випадковий вибір. Вказаний алгоритм працює доти доки перевірка на простоту буде виконана чи закінчиться час відведений для прогону цього алгоритму. Якщо за допомогою алгоритму Голдвассера—Килиана доведено простоту числа, тоді він також видає «сертифікат» простоти. 2) Метод комплексного множення, який запропоновано в роботі [13] взятий за основу методу, що запропонований в даному стандарті. Він передбачає: 1. По заданому порядку еліптичної кривої, яка визначена над полем 2. Знайти коефіцієнти мінімального полінома 3. Обчислити корені полінома Гільберта по модулю порядку поля 4. Визначити коефіцієнти еліптичної кривої над полем 5. Обирати випадкову точку на еліптичній кривій 6. При умові невиконання рівності
3) Стандартом ISO/IEC 15946-5 також передбачено застосування еліптичних кривих, які побудовано за допомогою білінійного спарювання, а саме Miyaji-Nakabayashi-Takano curve, Barreto-Naehrig curve, Freeman curve, Cocks-Pinch curve. Вказані методи побудування еліптичних кривих, що наведено в даному стандарті, базуються на розв’язанні порівняння 4) В стандарті ISO/IEC 15946-5 наведено алгоритм обчислення порядку еліптичної кривої за допомогою підняття. Вказаний алгоритм дозволяє, застосовуючи рівняння еліптичної кривої над полем
Таким чином, стандарт ISO/IEC 15946-5 забезпечує: 1. Базові методи побудови еліптичних кривих та перевірки їх на придатність до застосування в криптографічних перетвореннях були застосовані з стандартів IEEE P1363-2000, Standard Specifications for Public-Key Cryptography, ISO/IEC 9796 Information technology — Security techniques — Digital signature schemes, ISO/IEC 18032:2005, Information technology — Security techniques — Prime number generation; 2. Застосовані способи побудування еліптичних кривих за допомогою спарювання Вейля; 3. Методи, які застосовані для обчислення порядку еліптичної кривої та методи перевірки порядку еліптичної кривої на простоту є методами Скуфа та комплексного множення. 4. Метод побудування еліптичних кривих за допомогою піднняття, на відміну від методів Сатоо, алгебраїчно-геометричних значень, спроможний обчислити порядок кривої над розширенням поля малої характеристики за допомогою за допомогою рекурентних співвідношень, не виконуючи побудування еліптичної кривої над розширенням поля.
Основна література до 12.3 1. Schoof R. Counting points on an elliptic curve over finite fields / Schoof R. // Proc. Journees Arithmetiques. – 1995. – № 93. – P. 219–252.2. Бухштаб А.А. Теория чисел / А.А. Бухштаб М. Просвещение, 1996. ‑ 386с. 3. Бессалов А. Криптосистемы на эллиптических кривых / А. Бессалов, А. Телиженко. – К.: Політехніка, 2004. – 224 с. 4. Henri Cohen Handbook of Elliptic and Hyperelliptic Curve Cryptography / Henri Cohen Gerhard Frey.‑ Taylor & Francis Group, LLC, 2006 ‑ 843 P 5. Fouquet M. Isogeny volcanoes and the SEA algorithm In Algorithmic number theory / Fouquet M., Morain F. // Notes in Comput. Sci. – 2000, – Vol. 2369 – P. 276– 291.6. Skjernaa B. Satoh’s algorithm in characteristic 2 / Skjernaa B. // Mathematics of computation. – 2003. – № 72. – P. 477–487.
7. Blake. Ian F. Elliptic Curves in Cryptography / Blake. Ian F., Seroussi G, Nigel P. // Cambridge University Press – 1999. – P.121–130. 8. Morain F. Primality proving using elliptic curves: an update // Proceedings of ANTS III. 1998. (Lect. Notes in Comput. Sci.; V. 1423). P. 111—127. 9. Adleman L., Huang M.-D.A. Primality testing and abelian varietes over finite fields. 1992. (Lect. Notes in Math.; V. 1512). 10. Atkin A. O.L., Morain F. Elliptic curves and primality proving // Math. Comp. 1993. V. 61 (203). P. 29—67. 11. Satoh T. Canonical lifting of elliptic curves and p – adic point counting. (theoretical background) / Satoh T. // Department of Mathematics, Faculty of Science, Saitame University. – 2001. – P. 1–21. 12. Н. Соhen, C Frey Handbook of elliptic end hyperelliptic curve cryptografy // Carman end hall / CRC – 2006, – 843 p.13. L.C. Washington, “Elliptic Curves-Number Theory and Cryptography”, Chapman &Hall/CRC, edition, 2008
для забезпечення конфіденційності» Навчальні питання
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 , що рекомендовані FIPS 186-2-2000
, що рекомендовані FIPS 186-2-2000 , так і над розширенням поля характеристики два. Метод SEA базується на пошуку значення сліду ендоморфізму Фробеніуса з рівняння
, так і над розширенням поля характеристики два. Метод SEA базується на пошуку значення сліду ендоморфізму Фробеніуса з рівняння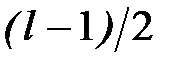 або поліномів степеня
або поліномів степеня  .
. . Недоліком цього метода є зростання коефіцієнтів поліномів
. Недоліком цього метода є зростання коефіцієнтів поліномів  при зростанні значення
при зростанні значення  . Наприклад, вільний член полінома
. Наприклад, вільний член полінома  дорівнює 157 000 000 000, а вільний член полінома
дорівнює 157 000 000 000, а вільний член полінома  дорівнює 1855425871872000000000 [3]. Обчислення порядку кривої, для полів вимірності від
дорівнює 1855425871872000000000 [3]. Обчислення порядку кривої, для полів вимірності від  до
до  за допомогою даного методу неможливо здійснити за прийнятний час завдяки наведеного недоліку.
за допомогою даного методу неможливо здійснити за прийнятний час завдяки наведеного недоліку. , з кофактором
, з кофактором  та великим простим порядком
та великим простим порядком  (160 біт та більше) визначити параметр
(160 біт та більше) визначити параметр  , де
, де 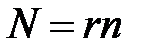 та квадратичний лишок
та квадратичний лишок  по модулю порядку поля;
по модулю порядку поля; -ого інваріанта (полінома Гільберта);
-ого інваріанта (полінома Гільберта); );
); та перевірити умову
та перевірити умову  , де
, де  - нескінчено віддалена точка. Якщо умова виконана, тоді криву знайдено. Якщо ні, тоді будують криву крутіння та виконують алгоритм знову;
- нескінчено віддалена точка. Якщо умова виконана, тоді криву знайдено. Якщо ні, тоді будують криву крутіння та виконують алгоритм знову; для кривої крутіння, де
для кривої крутіння, де  - випадкова точка кривої крутіння повторюють процедуру побудови еліптичної кривої для іншого кореня полінома Гільберта.
- випадкова точка кривої крутіння повторюють процедуру побудови еліптичної кривої для іншого кореня полінома Гільберта. , де
, де  є поліномом Гільберта для дискримінанту
є поліномом Гільберта для дискримінанту  , яке було застосованого для обчислення порядку еліптичної кривої методом комплексного множення.
, яке було застосованого для обчислення порядку еліптичної кривої методом комплексного множення.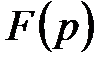 та його порядок, отримати значення порядку еліптичної кривої, яка визначена над полем
та його порядок, отримати значення порядку еліптичної кривої, яка визначена над полем  , базову точку цієї кривої. Даний алгоритм обчислення порядку еліптичної кривої відрізняється від ймовірнісних алгоритмів Сатоха та алгебраїчно-геометричних значень тим, що в вказаному алгоритмі обирають еліптичну криву, яка визначена над простим полем
, базову точку цієї кривої. Даний алгоритм обчислення порядку еліптичної кривої відрізняється від ймовірнісних алгоритмів Сатоха та алгебраїчно-геометричних значень тим, що в вказаному алгоритмі обирають еліптичну криву, яка визначена над простим полем  .
.


