
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Крипто перетворення в гіпереліптичних кривих
Першими пропозиціями щодо застосування гіпереліптичних кривих вочевидь необхідно вважати пропозиції Neal Koblitz – професора математики Вашингтонського університету [144]. Він є визнаним математиком, у тому числі з алгебраїчної геометрії, що включає й розділи теорії еліптичних і гіпереліптичних кривих. Деякий час вважалося, що застосування перетворень на гіпереліптичних кривих в криптографії суттєво обмежено через складності необхідних обчислень і, як наслідок, незадовільний рівень швидкодії. Значні результати у вирішенні цього протиріччя вніс професор Christof Paar (Германія). Ним вирішені задачі оптимізації обчислень на гіпереліптичних кривих 1–4 родів [146]. Так, він виконав оптимізацію формул складання та подвоєння дивізорів з використанням узагальненого метода Карацуби. Це дозволило підвищити швидкодії перетворень на гіпереліптичних кривих, досягти результатів, порівнюваних зі складністю перетворень на еліптичних кривих, а в деяких випадках і перевершити їх. Він також вів модифіковану метрику, більш точну. Останні дослідження значною мірою присвячені оптимізації складання та подвоєння за критерієм складності. В останні роки значні зусилля були спрямовані й на розробку теорії та практики криптографічної стійкості відносно криптографічних перетворень на гіпереліптичних кривих [145 - 150].
Таблиця 9.1 - Асиметричні криптографічні перетворення для реалізації направленого шифрування
Визначено, що основним параметром, від значення якого залежить криптографічна стійкість перетворень на еліптичних кривих, є порядок групи дивізорів гіпереліптичної кривої. На сьогодні для визначення порядку еліптичної кривої можуть бути застосовані два класи методів – l - адичні та p - адичні. В обох випадках теоретичною основою є поняття Дзета-функції та гіпотези Вейля. Чисельником Дзета-функції є характеристичний поліном ендоморфізма Фробеніуса. Далі, якщо гіпереліптична крива визначена над кінцевим полем Наведемо деякі поняття й визначення, що стосуються гіпереліптичних кривих, орієнтуючись на [145 150]. Визначення 1.1 Нехай F - кінцеве поле та нехай
де Коли g = 1, то ми маємо звичайну еліптичну криву. У цьому випадку нормований поліном За цієї умови еліптична крива Е в канонічній формі Веєрштрасса в афінних координатах може бути подана в такому вигляді:
причому коефіцієнти a, b, c Î F. Також відомо, що гіпереліптична крива не має особливих точок. Нехай На рис. 1.2 наведено приклад гіпереліптичної кривої над полем дійсних чисел. Для такої кривої точка на нескінченності лежить у проективній площині
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.40.207 (0.007 с.) |
 , то для визначення її порядку достатньо знати число точок, які задовольняють рівнянню кривої над усіма розширеннями поля
, то для визначення її порядку достатньо знати число точок, які задовольняють рівнянню кривої над усіма розширеннями поля  включно, де g - рід кривої. Нині найбільше розповсюдження отримали Р- адичні методи визначення порядку гіпереліптичних кривих.
включно, де g - рід кривої. Нині найбільше розповсюдження отримали Р- адичні методи визначення порядку гіпереліптичних кривих. - алгебраїчне замикання F. Тоді рівняння вигляду
- алгебраїчне замикання F. Тоді рівняння вигляду
 , (1.57)
, (1.57) - поліном степені не більше
- поліном степені не більше  ,
,  - нормований поліном степені
- нормований поліном степені  і немає розв’язків
і немає розв’язків  , які одночасно задовольняли б рівнянню
, які одночасно задовольняли б рівнянню  , і рівняння приватних похідних задовольняють умовам
, і рівняння приватних похідних задовольняють умовам 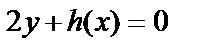 та
та  , визначає гіпереліптичну криву C роду
, визначає гіпереліптичну криву C роду  ) над F.
) над F. , (1.58)
, (1.58) – кінцева точка на гіпереліптичній кривій
– кінцева точка на гіпереліптичній кривій  . Протилежною точці
. Протилежною точці  є точка
є точка  . Також точка на нескінченності
. Також точка на нескінченності  є протилежною сама собі, тобто
є протилежною сама собі, тобто  . Якщо кінцева точка задовольняє умові
. Якщо кінцева точка задовольняє умові  , то така точка називається точкою спеціального вигляду, усі інші називаються звичайними.
, то така точка називається точкою спеціального вигляду, усі інші називаються звичайними. . Це єдина точка, що лежить на прямій у нескінченності, що задовольняє рівнянню, однорідному рівнянню гіпереліптичної кривої. Якщо
. Це єдина точка, що лежить на прямій у нескінченності, що задовольняє рівнянню, однорідному рівнянню гіпереліптичної кривої. Якщо  , то
, то 


