
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні труднощі розв’язування задач нелінійного програмуванняСодержание книги
Поиск на нашем сайте
Часто задачу нелінійного програмування намагаються звести до лінійного вигляду, що призводить до значних похибок. Наприклад, як правило, собівартість продукції y визначають за формулою:
Рисунок 8.3 У точках х 1 і х 3 величина собівартості для двох цих функцій однакова. Однак у всіх інших точках ці значення відрізняються, причому у точці х 2 у значній мірі, тобто на величину:
Отже, лінеаризація нелінійних процесів є досить складною математичною задачею. Зведення нелінійної задачі до лінійної дає змогу отримати симплексним методом розв’язок, близький до розв’язку початкової нелінійної задачі. Однак з вище розглянутого прикладу бачимо, що при побудові наближених лінійних задач можна отримати надто неточний розв’язок, який непридатний для використання. Навіть питання щодо існування розв’язку задачі нелінійного програмування потребує окремого дослідження. Розглянемо основні труднощі розв’язування нелінійних задач. 1. Для лінійних задач можна завжди знайти оптимальний розв’язок універсальним методом – симплексним. При цьому не існує проблеми стосовно доведення існування такого розв’язку, тобто в результаті застосування алгоритму симплексного методу завжди отримують один з таких варіантів відповіді: а) отримали оптимальний розв’язок; б) умови задачі суперечливі, тобто розв’язку не існує; в) цільова функція необмежена, тобто розв’язку також не існує. Для задач нелінійного програмування не існує універсального методу розв’язання, що зумовило розроблення значної кількості різних методів розв’язування окремих типів задач нелінійного програмування. Для кожного специфічного методу необхідно доводити існування розв’язку задачі та його єдиність, що також є досить складною математичною задачею. Відомі точні методи розв’язування нелінійних задач, але в такому разі існують труднощі обчислювального характеру, тобто навіть для сучасних ЕОМ такі алгоритми є досить трудомісткими, тому здебільшого для розв’язування нелінійних задач виправданим є застосування наближених методів.
2. Для задач лінійного програмування доведено наявність єдиного екстремуму, що досягається в одній (або кількох одночасно) з вершин багатогранника допустимих розв’язків задачі. Однак у задачах нелінійного програмування існують кілька локальних оптимумів, що потребує пошуку серед них глобального. На рис.8.4 маємо на відрізку, що зображений, локальні оптимуми у точках
Рисунок 8.4 Більшість наближених методів уможливлюють, як правило, знаходження локального оптимуму. Можна, звичайно, користуючись простим способом, визначити всі локальні оптимуми, а потім їх зіставленням знайти глобальний. Однак для практичних розрахунків такий метод є неефективним. Часто глобальний оптимум наближені методи «не уловлюють». Наприклад, у разі, коли глобальний оптимум знаходиться досить близько біля локального. Якщо відрізок 3. У задачах лінійного програмування точка оптимуму завжди була граничною точкою багатогранника допустимих планів. Для нелінійних задач точка, яка визначає оптимальний план, може бути як граничною, так і знаходитися всередині допустимої області розв’язків (планів), що було проілюстровано в прикладі 8.1. 4. Доведено, що множина допустимих планів задачі лінійного програмування завжди є опуклою. У разі, коли система обмежень задачі є нелінійною, вона може визначати множину допустимих розв’язків як неопуклу, або навіть складатися з довільних, не зв’язаних між собою частин (приклад 8.2). Одним з найпоширеніших прикладів зазначеної особливості є задачі цілочислового програмування. Нагадаємо, що вимога цілочисловості змінних задачі приводить до множини допустимих розв’язків, утвореної окремими точками, що зумовлює розглянуті вище ускладнення відшукання розв’язків такого типу задач. Кожна із зазначених особливостей задач вимагає застосування специфічних методів пошуку розв’язку, тому безперечно найскладнішими для розв’язування є задачі нелінійного програмування, в яких поєднується кілька або всі згадані особливості.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.241.124 (0.008 с.) |

 де х – обсяг виробництва. Ввівши заміну:
де х – обсяг виробництва. Ввівши заміну:  , маємо:
, маємо:  тобто приходимо до лінійної функції. За такої заміни похибок не допускають. Однак, якщо функцією собівартості буде
тобто приходимо до лінійної функції. За такої заміни похибок не допускають. Однак, якщо функцією собівартості буде  то використання замість неї деякої лінійної функції
то використання замість неї деякої лінійної функції 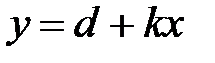 невиправдане, що видно з рис.8.3.
невиправдане, що видно з рис.8.3.
 .
.



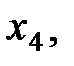




 глобальний – у точках
глобальний – у точках  та
та  .
.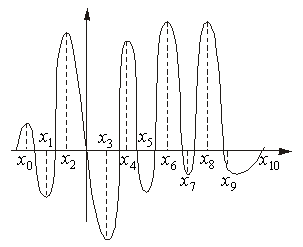
 поділити на десять підвідрізків і глобальний оптимум попаде у відрізок
поділити на десять підвідрізків і глобальний оптимум попаде у відрізок  (рис.8.4), а зліва від
(рис.8.4), а зліва від  та справа від
та справа від  крива
крива  буде зростати, то глобальний оптимум буде пропущеним.
буде зростати, то глобальний оптимум буде пропущеним.


