
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Економічна і математична постановка задачі нелінійного програмуванняСодержание книги
Поиск на нашем сайте
Класичний метод оптимізації. Метод множників Лагранжа Як уже згадувалось, для розв’язування задач нелінійного програмування не існує універсального методу, тобто до них необхідно застосовувати широке коло різних методів і обчислювальних алгоритмів. Вони в основному базуються на застосуванні диференційного числення і залежать від конкретної постановки задачі та форми економіко-математичної моделі. Методи розв’язування задач нелінійного програмування бувають прямі та непрямі. За допомогою прямих методів знаходження оптимальних планів здійснюють у напрямку найшвидшого збільшення (зменшення) значення цільової функції. Типовим представником цієї групи методів є градієнтні. Методика застосування непрямих методів передбачає зведення задачі до такої, оптимум якої слід знаходити простішими методами. Серед непрямих найкраще розробленими є методи розв’язування задач квадратичного та сепарабельного програмування. Найпростішими для розв’язування є задачі нелінійного програмування, в яких система обмежень складається лише з рівнянь. Метод множників Лагранжа Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення подальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних. У попередньому пункті наведена необхідна умова існування локального екстремуму неперервної та диференційовної функції двох змінних. Узагальнення необхідної умови існування локального екстремуму функції n змінних має аналогічний вигляд. Отже, для розв’язування задачі необхідно знайти вирази частинних похідних нової цільової функції за кожною змінною і прирівняти їх до нуля. В результаті отримаємо систему рівнянь. Її розв’язок визначає так звані стаціонарні точки, серед яких є і шукані екстремальні значення функції. Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:
за умов:
де функції Задача (8.6)-(8.7) полягає в знаходженні екстремуму функції Переходимо до задачі пошуку безумовного екстремуму. Теоретично доведено, що постановки та розв’язання таких задач еквівалентні. Замінюємо цільову функцію (8.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:
де Знайдемо частинні похідні і прирівняємо їх до нуля:
Друга група рівнянь системи (8.9) забезпечує виконання умов (8.7) початкової задачі нелінійного програмування. Система (8.9), як правило, нелінійна. Розв’язками її є Для діагностування стаціонарних точок і визначення типу екстремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій Узагальнення достатньої умови існування локального екстремуму для функції n змінних приводить до такого правила: за функцією Лагранжа виду (8.8) будується матриця Гессе, що має блочну структуру розмірністю
де О – матриця розмірністю Р – матриця розмірністю
Q – матриця розмірністю
Розглянемо ознаки виду екстремуму розв’язку системи (8.9). Нехай стаціонарна точка має координати 1. Точка 2. Точка Розглянемо задачу, розв’язок якої знайдемо методом множників Лагранжа. Приклад 8.3. Акціонерне товариство з обмеженою відповідальністю виділило 1200 га ріллі під основні сільськогосподарські культури – озиму пшеницю і цукрові буряки. У табл.8.1 маємо техніко-економічні показники вирощування цих культур: Таблиця 8.1
Необхідно знайти оптимальні площі посіву озимої пшениці та цукрових буряків. Нехай: х 1 – площа ріллі під озимою пшеницею, сотні га; х 2 – площа ріллі під цукровими буряками, сотні га. Звернемо увагу на те, що собівартість тонни пшениці та цукрових буряків залежить від відповідної площі посіву. Запишемо економіко-математичну модель цієї задачі. Критерієм оптимальності візьмемо максимізацію чистого доходу:
за умов:
Запишемо функцію Лагранжа:
Візьмемо частинні похідні і прирівняємо їх до нуля:
З цієї системи рівнянь визначаємо координати сідлових точок. З першого та другого рівняння знаходимо l1 і, прирівнюючи вирази, маємо:
або, скоротивши на 100 обидві частини і розкривши дужки, отримаємо:
Із останнього рівняння системи маємо: Підставимо вираз для
або
Отже,
Відповідно дістаємо:
Тобто отримали дві сідлові точки:
Перевіримо за допомогою достатньої умови існування екстремуму спочатку сідлову точку Матриця Гессе має такий вигляд:
За вищезазначеним правилом визначаємо головні мінори, починаючи з 2-го порядку (
Отже, головні мінори утворюють знакозмінний ряд та, починаючи з головного мінору 2-го порядку, наступний мінор визначається знаком Обчислимо значення цільової функції в цій точці:
Аналогічні обчислення для точки Отже, цільова функція набуде максимального значення, якщо озима пшениця вирощуватиметься на площі 647 га, а цукрові буряки – на площі 553 га. Метод множників Лагранжа може застосовуватися також у разі наявності обмежень на знаки змінних і обмежень-нерівностей. Розглянемо таку задачу в загальному вигляді:
причому всі функції, що входять у задачу, мають бути диференційовними хоча б один раз. Очевидно, що введення в ліві частини нерівностей системи обмежень задачі додаткових невід’ємних змінних Теорема Куна-Таккера Розглянутий метод множників Лагранжа уможливлює знаходження лише локальних сідлових точок функції Лагранжа. Теорема Куна-Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки. Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:
(Очевидно, що знак нерівності можна змінити на протилежний множенням лівої і правої частин обмеження на (– 1)). Теорема 8.1. (Теорема Куна-Таккера). Вектор Х* є оптимальним розв’язком задачі (8.22)-(8.24) тоді і тільки тоді, коли існує такий вектор
і функція мети Умови теореми Куна — Таккера виконуються лише для задач, що містять опуклі функції. Опуклі й вогнуті функції Наведемо основні означення та теореми. Нехай задано n -вимірний лінійний простір Rn. Функція
Якщо нерівність строга і виконується для Функція
Якщо нерівність строга і виконується для Слід зазначити, що опуклість та угнутість функції визначаються лише відносно опуклих множин у Теорема 8.2. Нехай Теорема 8.3. Нехай Як наслідок теореми можна показати, що коли Х замкнена, обмежена знизу, опукла множина, то глобального максимуму опукла функція f (X) досягає на ній у одній чи кількох точках (при цьому допускається, що в точці Х значення функції скінченне). Застосовуючи за розв’язування таких задач процедуру перебору крайніх точок, можна отримати точку локального максимуму, однак не можна встановити, чи є вона точкою глобального максимуму. Для угнутих функцій отримані результати формулюють так. Нехай f (X) – угнута функція, що задана на замкненій опуклій множині Градієнт угнутої функції f (X) у точках максимуму дорівнює нулю, якщо f (X) – диференційовна функція. Глобальний мінімум угнутої функції, якщо він скінченний на замкненій обмеженій зверху множині, має досягатися в одній чи кількох її крайніх точках за умови скінченності функції f (X) у кожній точці цієї множини. Опукле програмування Опукле програмування розглядає методи розв’язування задач нелінійного програмування, математичні моделі яких містять опуклі або угнуті функції. Загальний вигляд задачі опуклого програмування такий:
де Аналогічний вигляд має задача для опуклих функцій. Позначимо:
де Оскільки ці задачі еквівалентні, то нижче розглянемо задачу (8.27)-(8.29). Множина допустимих планів задачі, що визначається системою (8.28), є опуклою. Як наслідок теорем 8.2 та 8.3 справджується таке твердження: точка локального максимуму (мінімуму) задачі опуклого програмування (8.27)-(8.29) є одночасно її глобальним максимумом (мінімумом). Отже, якщо визначено точку локального екстремуму задачі опуклого програмування, то це означає, що знайдено точку глобального максимуму (мінімуму). У разі обмежень-нерівностей задачу опуклого програмування розв’язують, застосовуючи метод множників Лагранжа. Функція Лагранжа для задачі (8.27)-(8.29) має вид:
де Використовуючи теорему Куна-Таккера, маємо необхідні та достатні умови існування оптимального плану задачі опуклого програмування. Теорема 8.4. Якщо задано задачу нелінійного програмування виду (8.27)-(8.29), де функції (І) (ІІ) (ІІІ) (IV) Для задачі мінімізації (8.30)-(8.32), де всі функції
Економічна і математична постановка задачі нелінійного програмування Раніше було розглянуто методи розв’язування задач лінійного програмування. Ці методи найкраще розроблені, легко реалізуються на ПЕОМ, а тому набули широкого застосування в багатьох галузях науки, техніки та економіки. Проте лінійні моделі відображають лише певну й вельми обмежену сукупність властивостей навколишнього світу. Адже, скажімо, соціально-економічні процеси переважно не є лінійними. Галузі, об’єднання та окремі підприємства народного господарства функціонують і розвиваються за умов невизначеності, а тому адекватно їх можна описати нелінійними, стохастичними, динамічними моделями. Отже, для ефективного управління народним господарством в цілому, його галузями і окремими об’єктами господарювання потрібне застосування нелінійних економіко-математичних моделей та методів. Зауважимо, що сучасний рівень розвитку комп’ютерної техніки і методів математичного моделювання створює передумови для застосування нелінійних методів, а це може суттєво підвищити якість розроблюваних планів, надійність та ефективність рішень, які приймаються. Досить детально розглянута в лекціях, присвячених лінійному програмуванню, задача пошуку оптимальних обсягів виробництва ґрунтується на допущеннях про лінійність зв’язку між витратами ресурсів і обсягами виготовленої продукції; між ціною, рекламою та попитом тощо. Але такі зв’язки насправді є нелінійними, тому точніші математичні моделі доцільно формулювати в термінах нелінійного програмування. Нехай для деякої виробничої системи необхідно визначити план випуску продукції за умови найкращого способу використання її ресурсів. Відомі загальні запаси кожного ресурсу, норми витрат кожного ресурсу на одиницю продукції та ціни реалізації одиниці виготовленої продукції. Критерії оптимальності можуть бути різними, наприклад, максимізація виручки від реалізації продукції. Така умова подається лінійною залежністю загальної виручки від обсягів проданого товару та цін на одиницю продукції. Однак, загальновідомим є факт, що за умов ринкової конкуренції питання реалізації продукції є досить складним. Обсяг збуту продукції визначається передусім її ціною, отже, як цільову функцію доцільно брати максимізацію не всієї виготовленої, а лише реалізованої продукції. Необхідно визначати також і оптимальний рівень ціни на одиницю продукції, за якої обсяг збуту був би максимальним. Для цього її потрібно ввести в задачу як невідому величину, а обмеження задачі мають враховувати зв’язки між ціною, рекламою та обсягами збуту продукції. Цільова функція в такому разі буде виражена добутком двох невідомих величин: оптимальної ціни одиниці продукції на оптимальний обсяг відповідного виду продукції, тобто буде нелінійною. Отже, маємо задачу нелінійного програмування. Також добре відома транспортна задача стає нелінійною, якщо вартість перевезення одиниці товару залежить від загального обсягу перевезеного за маршрутом товару. Тобто коефіцієнти при невідомих у цільовій функції, що в лінійній моделі були сталими величинами, залежатимуть від значень невідомих (отже, самі стають невідомими), що знову приводить до нелінійності у функціоналі. І нарешті, будь-яка задача стає нелінійною, якщо в математичній моделі необхідно враховувати умови невизначеності та ризик. Як показник ризику часто використовують дисперсію, тому для врахування обмеженості ризику потрібно вводити нелінійну функцію в систему обмежень, а мінімізація ризику певного процесу досягається дослідженням математичної моделі з нелінійною цільовою функцією. Загальна задача математичного програмування формулюється так: знайти такі значення змінних xj
за умов:
Якщо всі функції
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.24.148 (0.012 с.) |

 (8.6)
(8.6)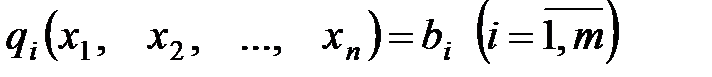 , (8.7)
, (8.7) і
і 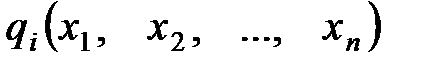 мають бути диференційовними.
мають бути диференційовними.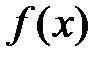 за умов виконання обмежень
за умов виконання обмежень  .
. (8.8)
(8.8) – деякі невідомі величини, що називаються множниками Лагранжа.
– деякі невідомі величини, що називаються множниками Лагранжа.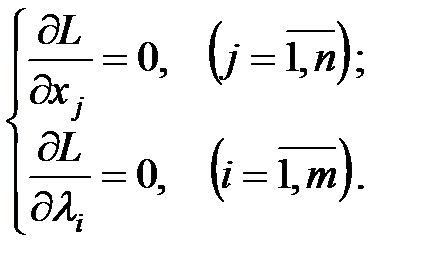
 (8.9)
(8.9)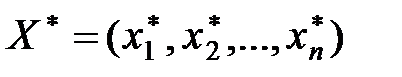 і
і  – стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (8.6)-(8.7) або можуть бути точками перегину (сідловими точками).
– стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (8.6)-(8.7) або можуть бути точками перегину (сідловими точками). існують другі частинні похідні і вони неперервні).
існують другі частинні похідні і вони неперервні). :
: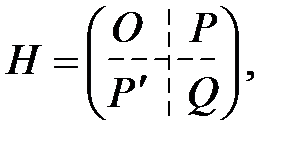
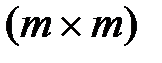 , що складається з нульових елементів,
, що складається з нульових елементів,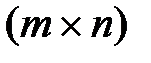 , елементи якої визначаються так:
, елементи якої визначаються так: ,
, – транспонована матриця до Р розмірністю
– транспонована матриця до Р розмірністю 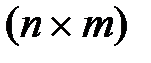 ,
,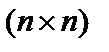 виду:
виду: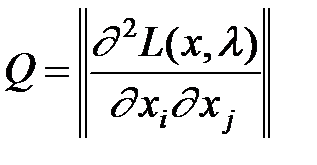 , де
, де  .
. і
і  .
.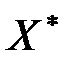 є точкою максимуму, якщо, починаючи з головного мінору порядку (m +1), наступні (n – m) головних мінорів матриці Н утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником
є точкою максимуму, якщо, починаючи з головного мінору порядку (m +1), наступні (n – m) головних мінорів матриці Н утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником  .
.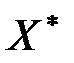 є точкою мінімуму, якщо, починаючи з головного мінору порядку (m +1), знак наступних (n – m) головних мінорів матриці Н визначається множником
є точкою мінімуму, якщо, починаючи з головного мінору порядку (m +1), знак наступних (n – m) головних мінорів матриці Н визначається множником  .
.

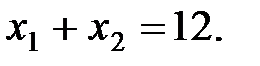


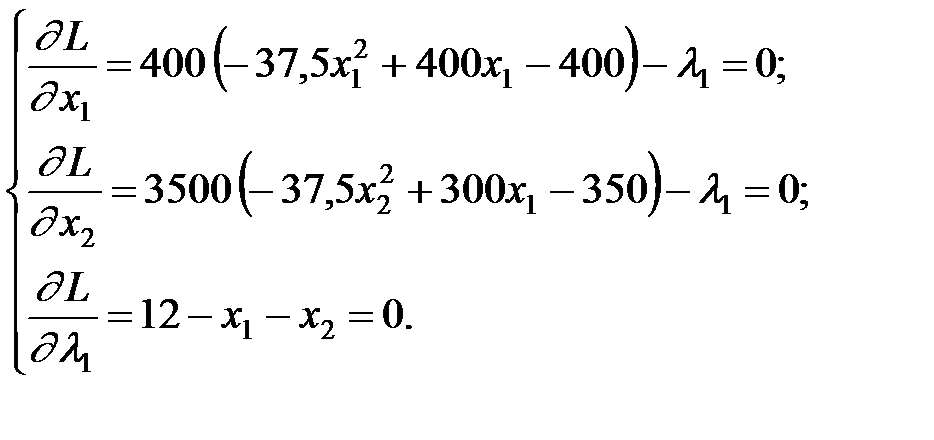
 (8.10)
(8.10) . (8.11)
. (8.11) .
. у рівність (8.11). Отримаємо:
у рівність (8.11). Отримаємо: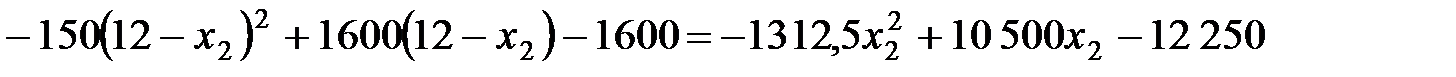
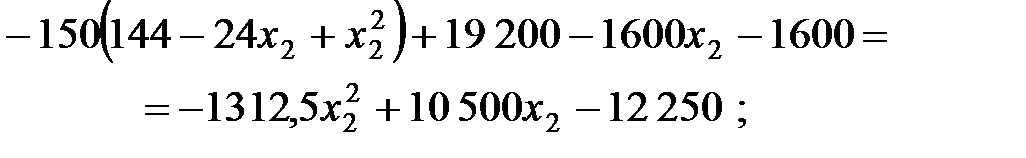

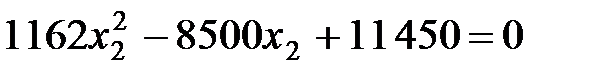 ;
;
 .
. (553 га);
(553 га);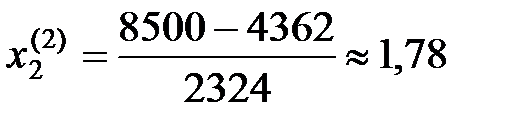 (178 га).
(178 га). га);
га); га).
га).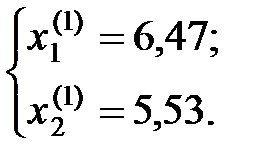

 .
. .
.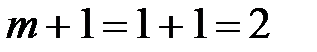 ):
): ,
,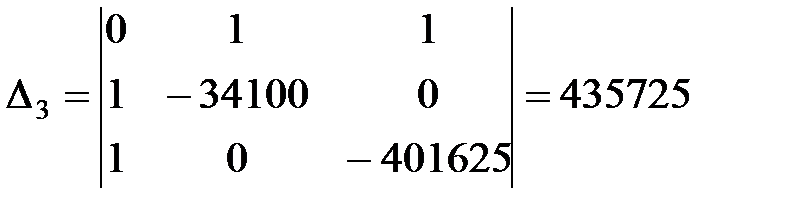 .
.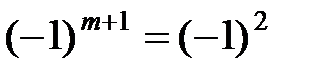 , тобто
, тобто  є точкою максимуму.
є точкою максимуму.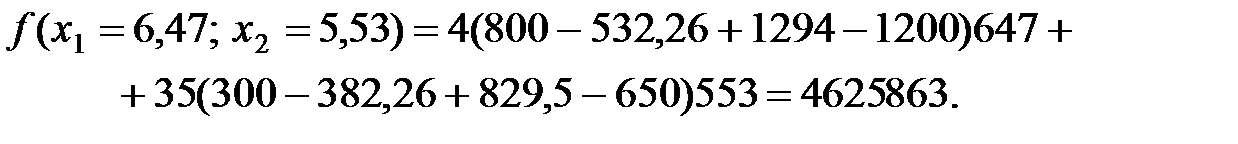
 показують, що вона не є екстремальною.
показують, що вона не є екстремальною. ,
,
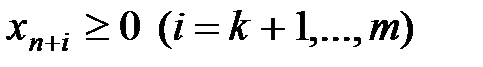 перетворює початкову задачу в таку, що містить лише обмеження-рівності, тобто яка за формою та методом розв’язування збігатиметься з задачею (8.6)-(8.7).
перетворює початкову задачу в таку, що містить лише обмеження-рівності, тобто яка за формою та методом розв’язування збігатиметься з задачею (8.6)-(8.7).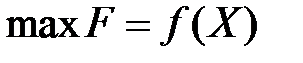 , (8.22)
, (8.22) , (8.23)
, (8.23) . (8.24)
. (8.24) , що при
, що при  для всіх
для всіх  точка
точка  є сідловою точкою функції Лагранжа
є сідловою точкою функції Лагранжа ,
, для всіх
для всіх  угнута, а функції
угнута, а функції  – опуклі.
– опуклі. , що задана на опуклій множині
, що задана на опуклій множині  , називається опуклою, якщо для будь-яких двох точок
, називається опуклою, якщо для будь-яких двох точок  та
та  з множини X і будь-яких значень
з множини X і будь-яких значень  виконується співвідношення:
виконується співвідношення: . (8.25)
. (8.25) , то функція
, то функція  називається строго опуклою.
називається строго опуклою. , яка задана на опуклій множині
, яка задана на опуклій множині  , називається вогнутою, якщо для будь-яких двох точок
, називається вогнутою, якщо для будь-яких двох точок  та
та  з множини X і будь-якого
з множини X і будь-якого  справджується співвідношення:
справджується співвідношення: . (8.26)
. (8.26) , то функція
, то функція  називається строго угнутою.
називається строго угнутою. , оскільки за наведеними означеннями разом з двома будь-якими точками
, оскільки за наведеними означеннями разом з двома будь-якими точками  та
та  множині X належать також точки їх лінійної комбінації:
множині X належать також точки їх лінійної комбінації:  для всіх значень
для всіх значень  , що можливо лише у разі, коли множина X є опуклою.
, що можливо лише у разі, коли множина X є опуклою. – опукла функція, що задана на замкненій опуклій множині X, тоді будь-який локальний мінімум
– опукла функція, що задана на замкненій опуклій множині X, тоді будь-який локальний мінімум 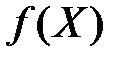 на цій множині є і глобальним.
на цій множині є і глобальним. – опукла функція, що визначена на опуклій множині Х, і крім того, вона неперервна разом з частинними похідними першого порядку в усіх внутрішніх точках Х. Нехай
– опукла функція, що визначена на опуклій множині Х, і крім того, вона неперервна разом з частинними похідними першого порядку в усіх внутрішніх точках Х. Нехай  – точка, в якій
– точка, в якій  . Тоді в точці
. Тоді в точці  досягається локальний мінімум, що збігається з глобальним.
досягається локальний мінімум, що збігається з глобальним. . Тоді будь-який локальний максимум f (X) на множині Х є глобальним. Якщо глобальний максимум досягається в двох різних точках множини, то він досягається і на нескінченній множині точок, що лежать на відрізку, який сполучає ці точки. Для строго угнутої функції існує єдина точка, в якій вона досягає глобального максимуму.
. Тоді будь-який локальний максимум f (X) на множині Х є глобальним. Якщо глобальний максимум досягається в двох різних точках множини, то він досягається і на нескінченній множині точок, що лежать на відрізку, який сполучає ці точки. Для строго угнутої функції існує єдина точка, в якій вона досягає глобального максимуму. , (8.27)
, (8.27) ,
,  ; (8.28)
; (8.28) , (8.29)
, (8.29) ,
,  – угнуті функції.
– угнуті функції. , тоді
, тоді  , і маємо:
, і маємо: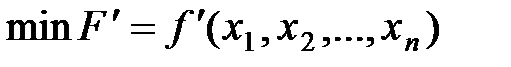 , (8.30)
, (8.30)
 ; (8.31)
; (8.31) , (8.32)
, (8.32) ,
,  – опуклі функції.
– опуклі функції. (8.33)
(8.33) – множники Лагранжа.
– множники Лагранжа.
 диференційовні і вгнуті по Х, то для того, щоб вектор
диференційовні і вгнуті по Х, то для того, щоб вектор  був розв’язком цієї задачі, необхідно і достатньо, щоб існував такий вектор
був розв’язком цієї задачі, необхідно і достатньо, щоб існував такий вектор 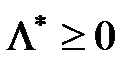 , що пара (
, що пара ( ,
, 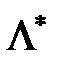 ) була б сідловою точкою функції Лагранжа, тобто щоб виконувалися умови:
) була б сідловою точкою функції Лагранжа, тобто щоб виконувалися умови: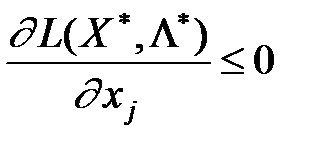 ,
,  ; (8.34)
; (8.34) ,
,  ; (8.35)
; (8.35) ,
,  ; (8.36)
; (8.36) ,
,  . (8.37)
. (8.37)
 диференційовні і опуклі по Х, маємо умови, аналогічні вищенаведеним, але зі знаком «≥» в нерівностях (8.35) та (8.37).
диференційовні і опуклі по Х, маємо умови, аналогічні вищенаведеним, але зі знаком «≥» в нерівностях (8.35) та (8.37). , щоб цільова функція набувала екстремального (максимального чи мінімального) значення:
, щоб цільова функція набувала екстремального (максимального чи мінімального) значення: (8.1)
(8.1) (
( ); (8.2)
); (8.2)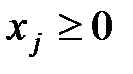
 . (8.3)
. (8.3) та
та  ,
, 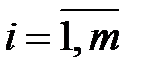 є лінійними, то це задача лінійного програмування, інакше (якщо хоча б одна з функцій є нелінійною) маємо задачу нелінійного програмування.
є лінійними, то це задача лінійного програмування, інакше (якщо хоча б одна з функцій є нелінійною) маємо задачу нелінійного програмування.


