
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 10. Линейные неоднородные уравнения с постоянными коэффициентами и с правой частью специального вида. Метод подбора или метод неопределенных коэффициентов.
Дано уравнение
С постоянными вещественными коэффициентами Общее решение неоднородного уравнения или уравнения с правой частью
Для правых частей специального вида частное решение можно найти так называемым методом подбора. Общий вид правой части
где В этом случае частное решение
где Частные случаи I. 1) если число
где 2) число
II. если 1)
2) число
III. если 1) число
2) число
Замечание. Первые два вида являются частными случаями III вида. Пример 16. Найти общее решение уравнения Решение. Характеристической уравнение (х.у.)
Находим частное решение
А, В, С – неопределенные (неизвестные) коэффициенты. Подставляя
Откуда
Решая систему, находим
Пример 17. Решить уравнение Решение.
Подставляя
Приравнивая коэффициенты при
Замечание. Если правая часть уравнения Упражнения. Определить вид частного решения. 1) 2) 3) 4)
Для следующих линейных неоднородных дифференциальных уравнений определить вид частного решения не находя числовых значений коэффициентов:
Упражнения. Решить уравнения. 1) 2) 3) 4) Замечание. Следует найти отдельно два частных решения Задача 11. Решить следующие линейные неоднородные уравнения с правой частью специального вида методом подбора частного решения по виду правой части.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.190.144 (0.011 с.) |
 (1)
(1) .
. равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения
равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения 
 .
. (2),
(2), многочлены степени
многочлены степени  соответственно.
соответственно. (3),
(3), – многочлены от
– многочлены от  –й степени общего вида с неопределенными коэффициентами, а
–й степени общего вида с неопределенными коэффициентами, а  – кратность корня
– кратность корня  характеристического уравнения (если
характеристического уравнения (если 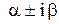 не является корнем характеристического уравнения, то
не является корнем характеристического уравнения, то  ).
). .
. не является корнем х.у., то
не является корнем х.у., то ,
, – многочлен той же степени, что и
– многочлен той же степени, что и  , но с неопределенными коэффициентами.
, но с неопределенными коэффициентами. кратности
кратности  .
. , то
, то не является корнем х.у., то
не является корнем х.у., то ,
,  .
. .
. , то
, то не является корнем х.у., то
не является корнем х.у., то .
. .
. .
. имеет различные корни
имеет различные корни  , поэтому общее решение
, поэтому общее решение .
. ; это многочлен
; это многочлен 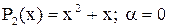 – не является корнем х.у., поэтому
– не является корнем х.у., поэтому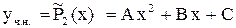 ,
,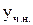 в уравнение, получим
в уравнение, получим .
.
 . Следовательно,
. Следовательно,  и общее решение будет
и общее решение будет .
.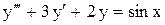 .
.
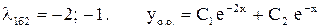 .
. – нее является корнем х.у., поэтому
– нее является корнем х.у., поэтому .
. .
. слева и справа, получим систему уравнений относительно неизвестных А и В.
слева и справа, получим систему уравнений относительно неизвестных А и В.

 .
. .
. .
. (1) имеет вид:
(1) имеет вид:  , то частное решение уравнения (1)
, то частное решение уравнения (1)  , где
, где  – частное решение уравнения
– частное решение уравнения  ;
;  – частное решение уравнения
– частное решение уравнения  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ: 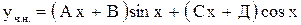 .
. .
.
 .
.
 .
.
 .
.
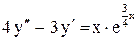 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
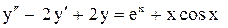 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. соответствующие
соответствующие  , но можно найти их и вместе.
, но можно найти их и вместе.


