
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обыкновенные дифференциальные уравненияСтр 1 из 5Следующая ⇒
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Методические указания и варианты расчётной работы для студентов 1-2 курсов технических специальностей.
Для выполнения типового расчета по обыкновенным дифференциальным уравнения (д. у.) рекомендуется изучить теоретический материал по следующим вопросам: Дифференциальные уравнения первого и высших порядков [1-10]. 1. Основные понятия теории д.у. Задача Коши для д.у. первого порядка. Формулировка теоремы существования и единственности решения задачи Коши. 2. Д.у. первого порядка: с разделяющимися переменными, однородные и приводящиеся к однородным. 3. Линейные уравнения первого порядка, уравнения Бернулли. 4. Уравнения в полных дифференциалах. 5. Д.у. высших порядков, допускающие понижение порядка. 6. Линейный дифференциальный оператор, его свойства. Линейное однородное дифференциальное уравнение, свойства его решений. 7. Условие линейной независимости решений линейного однородного дифференциального уравнения. 8. Линейное однородное д.у. Фундаментальная система решений. Структура общего решения. 9. Линейное неоднородное д.у. Структура общего решения. 10. Метод Лагранжа вариации произвольных постоянных. 11. Линейные однородные д.у. с постоянными коэффициентами (случай простых и кратных корней характеристического уравнения вещественных и комплексных). 12. Линейные неоднородные д.у. с постоянными коэффициентами с правыми частями специального вида. Метод подбора частного решения по виду правой части с помощью неопределенных коэффициентов. 13. Решение линейных неоднородных уравнений с правой частью неспециального вида методом Коши.
ЗАДАЧИ № 1-15
Задачи № 1-№ 5. Уравнения первого порядка: с разделяющимися переменными и приводящиеся к ним, однородные и приводящиеся к однородным, линейным уравнения, уравнение Бернулли, уравнение в полных дифференциалах. Задача № 6. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и указать в общем виде метод решения. Задача № 7. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и решить. Задача № 8. Уравнения, допускающие понижение порядка. Задача № 9. Однородные линейные д.у. второго и высших порядков. Задача № 10 - №11. Неоднородные линейные уравнения с постоянными коэффициентами с правой частью специального вида.
Задача № 12. Метод Лагранжа, метод вариации постоянных. Задача № 13. Решить методом Коши задачу Коши для линейных неоднородных д.у. с непрерывной правой частью неспециального вида. Задача № 14. Решить методом Коши задачу Коши. Задача № 15. Решить методом Коши задачу Коши для д.у. с разрывной правой частью. Задача № 16. Решить неоднородную систему ОДУ методом вариации произвольных постоянных.
Пример 1. Решить уравнение Решение. Разделим обе части уравнения на произведение
Получим уравнение с разделенными переменными. Интегрируя его, найдем
После потенцирования получим
Откуда Обозначая Получили общий интеграл этого уравнения. Функции Ответ: Пример 2. Найти частное решение уравнения Решение. Имеем Разделяем переменные, для этого обе части уравнения делим на произведение
Интегрируя, найдем общий интеграл
в качестве производной константы После потенцирования, получим Найдем константу
Искомое частное решение или решение задачи Коши Ответ: Упражнения. Решить уравнения 1. 2. 3. 4. Решить уравнения с разделяющимися переменными:
Пример 3. Решить уравнение Решение. Запишем уравнение в виде Разделяя переменные, будем иметь Отсюда интегрированием находим
Ответ: Упражнения. Решить уравнения 1. 2. 3. 4.
Решить однородные дифференциальные уравнения.
Пример 4. Решить уравнение Решение. Вид уравнения нормальный
Ответ:
Упражнения. Решить уравнения 1. 2. Приводим к виду 3. 4.
Уравнение линейное относительно функции
Решить линейные дифференциальные уравнения первого порядка:
Пример 5. Решить уравнение Бернулли Приведем уравнение к виду
Обе части уравнения умножим на
Получили Поэтому Ответ: Упражнения. Решить уравнения 1. 2. 3. Уравнение следует переписать в виде
4. Обе части уравнения следует умножить на Решить уравнения Бернулли:
Пример 6. Решить уравнение Решение. Проверим является ли данное уравнение уравнением в полных дифференциалах
Получили, что Найдем функцию
Из первого уравнения, интегрированием по
где Частная производная
Отсюда
Ответ:
Упражнения. Решить уравнения 1. 2. 3. 4.
Проинтегрировать уравнения в полных дифференциалах:
Пример 8. Найти общее решение уравнения Решение.
Пример 9. Решить уравнение Решение. Данное уравнение не содержит искомой функции Разделяя переменные, найдем
Ответ: Пример 10. Решить уравнение Решение. Данное уравнение III типа. Введем обозначение
Заменяя
Замечание. При решении задачи Коши для уравнений высших порядков целесообразно определять значения постоянных
Пример 11. Решить задачу Коши Решение. Полагая Разделяя переменные, найдем ного бинома, случай неберущегося интеграла. Но если использовать начальные условия
Ответ: Упражнения. Решить уравнения. 1) 2) 3) 4)
Решить уравнения, допускающие понижение порядка
Геометрические приложения.
В геометрических задачах, в которых требуется найти уравнение кривой по данному свойству ее касательной, нормали или площади криволинейной трапеции, используется геометрическое истолкование производной (угловой коэффициент касательной) и интеграл с переменным пределом (площадь криволинейной трапеции с подвижной ограничивающей ординатой), а так же следующие общие формулы для определения длин отрезков касательной t, нормали n, подкасательной St и поднормали Sn.
Пример 21. Найти такую кривую, проходящую через точку (0, - 2), чтобы угловой коэффициент касательной в любой ее точке равнялся ординате этой точки, увеличенной в три раза. Решение. Допустим, что искомая кривая описывается функций Пример 22. материальная точка массой Решение. По второму закону Ньютона Имеем Найдем скорость, которая будет спустя минуту после начала движения:
Пример 23. Тело массы
Решение. Уравнение движения имеет вид
Пример 24. К источнику с э. д. с. равной Решение. По условию задачи
Уравнение (4) аналогично уравнению свободных механических колебаний с учетом сопротивления среды. Решим уравнение (4). Характеристическое уравнение имеет корни Если Если же где положено
и, таким образом, начальные условия запишутся в виде
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.20.56 (0.122 с.) |


 .
. .
. или
или  .
. .
. , будем иметь
, будем иметь  или
или  .
. ,
,  и
и  - являются частными решениями.
- являются частными решениями. - общий интеграл.
- общий интеграл. , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  .
. или
или  .
.
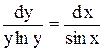 .
.
 взяли
взяли  .
. или
или  - общее решение исходного уравнения.
- общее решение исходного уравнения.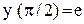 ,
,  или
или отсюда
отсюда  .
. .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  или
или  .
. .
.
 .
.
 .
.
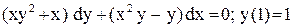 .
.
 .
.
 .
.
 .
.
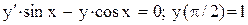 .
.
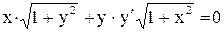 .
.
 .
.
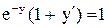 .
.
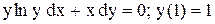 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
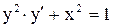 .
.
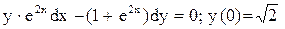 .
.
 .
.
 .
.
 .
.
 .
.
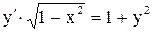 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
. , разделив на
, разделив на  обе части уравнения. Сделаем замену
обе части уравнения. Сделаем замену 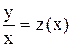 . Тогда
. Тогда  ,
,  . Получим
. Получим  или
или  .
. .
.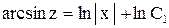
 или
или , так как
, так как  , то обозначая
, то обозначая  , получим
, получим . Заменяя
. Заменяя  на
на  , будем иметь общий интеграл
, будем иметь общий интеграл , отсюда
, отсюда  - общее решение.
- общее решение. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Соберем коэффициенты при
. Соберем коэффициенты при 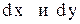
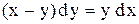 . Ответ:
. Ответ:  .
. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
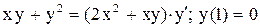 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.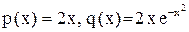 .
.
 .
.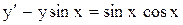 . Ответ:
. Ответ:  .
. .
. ,
,  и решаем по формуле, которая была выведена на лекциях (повторить, потому, что вывод спрашивают!)
и решаем по формуле, которая была выведена на лекциях (повторить, потому, что вывод спрашивают!)  . Ответ:
. Ответ: 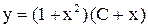 .
. . Ответ:
. Ответ:  .
.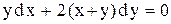 . Ответ:
. Ответ:  .
.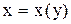 . Приводим его к виду
. Приводим его к виду или
или  .
. .
.
 .
.
 ;
;  .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
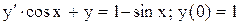 .
.
 .
.
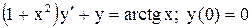 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
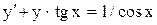 .
.
 .
.
 .
.
 .
.
 .
.
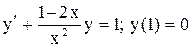 .
.
 .
.
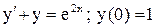 .
.
 .
.
 .
.
 .
. и сделаем замену
и сделаем замену 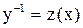 , причем,
, причем,  , получим
, получим 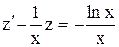 - это линейное уравнение относительно
- это линейное уравнение относительно  .
.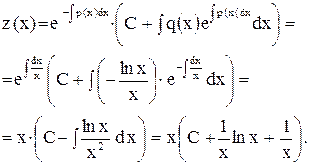
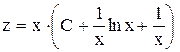 .
. .
. .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. или
или  - это уравнение Бернулли относительно функции
- это уравнение Бернулли относительно функции 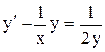 . Ответ:
. Ответ:  .
. и сделать замену
и сделать замену  .
. .
.
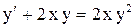 .
.
 .
.
 .
.
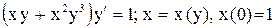 .
.
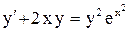 .
.
 .
.
 .
.
 .
.
 .
.
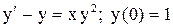 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
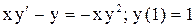 .
.
 .
.
 .
.
 .
.
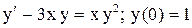 .
.
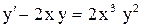 .
.
 .
.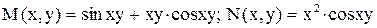 .
.
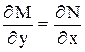 , условие (2) выполнено, значит данное уравнение в полных дифференциалах.
, условие (2) выполнено, значит данное уравнение в полных дифференциалах.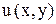 . Для этого имеем систему:
. Для этого имеем систему:

 ,
, - произвольная функция (вместо постоянной интегрирования С берем функцию
- произвольная функция (вместо постоянной интегрирования С берем функцию  , найденной функции
, найденной функции 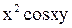 , что дает
, что дает ,
,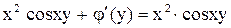 .
. ,
, - общий интеграл.
- общий интеграл. , где
, где  .
. . Ответ:
. Ответ: 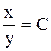 .
.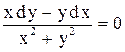 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.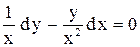 . Ответ:
. Ответ: 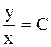 .
.
 ,
, уравнение в полных дифференциалах.
уравнение в полных дифференциалах. .
.
 .
.
 .
.
 .
.
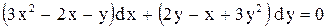 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
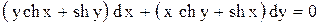 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
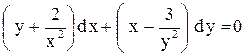 .
.
 .
.
 .
.
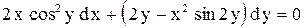 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.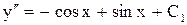 ,
, ,
, .
. .
. , тогда
, тогда  . После этого уравнения примет вид
. После этого уравнения примет вид  .
. , заменяя на
, заменяя на  , получим
, получим  . Интегрируя последовательно, будем иметь
. Интегрируя последовательно, будем иметь
 .
. .
. , получим
, получим  - уравнение Бернулли. Подстановкой
- уравнение Бернулли. Подстановкой  оно сводится к линейному уравнению
оно сводится к линейному уравнению  .
.
 , получим
, получим  . Интегрируя, будем иметь
. Интегрируя, будем иметь или
или  ;
;  .
. в процессе решения, а не после нахождения общего решения уравнения.
в процессе решения, а не после нахождения общего решения уравнения.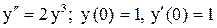 .
. , получим
, получим  или
или  откуда
откуда  ;
;  .
. . Интеграл в правой части в элементарных функциях не вычисляется, как интеграл от дифференциаль-
. Интеграл в правой части в элементарных функциях не вычисляется, как интеграл от дифференциаль- , то
, то  и тогда
и тогда
 .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ: 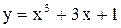 .
. .
.
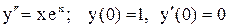 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
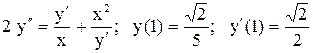 .
.
 .
.
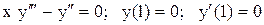 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
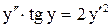 .
.
 .
.
 .
.
 .
.
 .
.
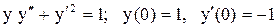 .
.
 .
.
 .
.

 ,
,  ,
,

 .
.
 . Найдем ее. Угловой коэффициент
. Найдем ее. Угловой коэффициент  равен
равен  . Имеем
. Имеем  и начальное условие
и начальное условие  . Решим уравнение
. Решим уравнение  или
или  . Используя начальное условие, получим
. Используя начальное условие, получим  .
. кг движется прямолинейно под действием силы, прямо пропорциональной времени, отсчитываемому от момента
кг движется прямолинейно под действием силы, прямо пропорциональной времени, отсчитываемому от момента  , и обратно пропорционально скорости движения точки. В момент
, и обратно пропорционально скорости движения точки. В момент  м/с, а сила
м/с, а сила  Н. Какова будет скорость спустя минуту после начала движения?
Н. Какова будет скорость спустя минуту после начала движения? , где k – коэффициент пропорциональности. Найдем k из условия, что в момент
, где k – коэффициент пропорциональности. Найдем k из условия, что в момент  скорость равнялась
скорость равнялась  .
. . Решим уравнение
. Решим уравнение  .Произвольную постоянную С найдем из условия: в момент
.Произвольную постоянную С найдем из условия: в момент  , т.е.
, т.е.  ,
,  .
. .
. скользит по горизонтальной плоскости под действием толчка, давшего начальную скорость
скользит по горизонтальной плоскости под действием толчка, давшего начальную скорость 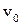 . На тело действует сила трения, равная
. На тело действует сила трения, равная  . Найти расстояние, которое тело способно пройти.
. Найти расстояние, которое тело способно пройти. . Найдем решение этого уравнения при начальных
. Найдем решение этого уравнения при начальных  . Имеем
. Имеем 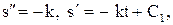
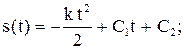
 найдем из начальных условий:
найдем из начальных условий:  . Получим
. Получим  . Найдем момент времени t, при котором тело остановится:
. Найдем момент времени t, при котором тело остановится:  . За время
. За время 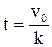 пройденный путь
пройденный путь  .
. подключается контур, состоящий из последовательно соединенных катушки индуктивности L, омического сопротивления R и емкости С. Найти ток I в цепи как функцию времени t, если в начальный момент ток в контуре и заряд конденсатора равны нулю.
подключается контур, состоящий из последовательно соединенных катушки индуктивности L, омического сопротивления R и емкости С. Найти ток I в цепи как функцию времени t, если в начальный момент ток в контуре и заряд конденсатора равны нулю. . В этом случае
. В этом случае  и уравнение (2) получается однородным
и уравнение (2) получается однородным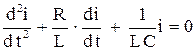 (4)
(4)
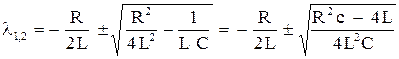 .
. , то оба корня
, то оба корня  действительные и общее решение есть функция непериодическая. Соответственно апериодическим будет и ток. Никаких электрических колебаний в цепи не произойдет так же и при
действительные и общее решение есть функция непериодическая. Соответственно апериодическим будет и ток. Никаких электрических колебаний в цепи не произойдет так же и при  .
. , то корни х.у. будут комплексно-сопряженными и общее решение
, то корни х.у. будут комплексно-сопряженными и общее решение  ,
, , определяет электрические колебания.
, определяет электрические колебания.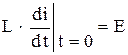 , откуда
, откуда  ,
, . (5)
. (5) найдем, используя начальные условия (5)
найдем, используя начальные условия (5)


