
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое представление детерминированных искусственных динамических систем
Временные характеристики системы В динамической системе при одном и том же входном значении в разные моменты времени выходной сигнал зависит от того, в какой последовательности подавались входные значения. Динамические системы, в отличие от статических, помнят свое прошлое состояние, то есть обладают памятью. Поэтому в записи модели динамических систем должна присутствовать производная по времени, связывающая прошлое состояние системы с настоящим. Чем большей памятью обладает система, тем больше состояний из прошлого влияют на настоящее, тем большая степень производной используется в записи модели. Детерминированные динамические системы- это прежде всего технические системы, созданные человеком на основе тех или иных физических законов, описываемых в виде уравнений Ньютона, Кирхгофа, Максвелла и т.п. Сигналы, исходная информация для моделирования может быть получена в аналоговом или дискретном виде.
Для численного представления на компьютере аналоговый сигнал переводят в дискретный вид и далее используют в виде таблицы, таблица 2.1.
Таблица 2.1- Табличное представление временного сигнала
Таблица отсчтетов может быть получена также и в процессе эксперимента, снимаются показания приборов в отдельные моменты времени. Совокупность значений переменной, упорядоченных во времени, называют динамическим рядом. Частоту дискретизации принимают такой, чтобы, если это необходимо, не потерять высокочастотные составляющие в сигнале, т.к. она может иметь определенную ценность для описания системы. Дискретные значения аппроксимируют зависмостью в виде дифференциального уравнения. Чем большая степень старшей производной присутствует в записи модели, тем больший порядок динамической системы, тем глубже ее память, и тем больше коэффициентов (параметров) надо определить, чтобы идентифицировать систему. Допустим, что на вход системы, до этого находившейся в нулевых начальных условиях, подали единичный сигнал X (t), как показано на рисунке 2.2 [3].
Рисунок 2.2- Входной и выходной сигнал системы первого порядка
Принято считать, что выходной сигнал системы будет экспоненциальным, т.е. системой первого порядка (или звеном первого порядка). Для ее описания достаточно одной производной (а в решении модели будет присутствовать один интеграл):
У такой системы два параметра — T и k. Чтобы определить, является ли кривая экспонентой, в каждой ее точке проводится касательная до пересечения с линией установившегося уровня (на рисунке 2.2 - это линия y (t) = k): в случае, если кривая является экспонентой, величина T в любой точке будет постоянной. T характеризует инерционность системы (память). При ее малой величине система слабо зависит от предыстории и вход мгновенно заставляет измениться выход. При большом значении T система медленно реагирует на входной сигнал, а при очень большом значении T система выдает неизменный выходной сигнал, практически не реагируя на входные воздействия. Коэффициент k характеризует способность системы к усилению (при k < 1 — к ослаблению) уровня входного сигнала. Чтобы определить коэффициент k на графике, достаточно дождаться успокоения сигнала на выходе системы и вычислить отношение уровня выходного сигнала к уровню входного. Для оценки динамических свойств системы и отдельных ее звеньев принято исследовать их реакцию на типовые входные воздействия, которые наиболее полно отражают особенности реальных возмущений. Это позволяет сравнивать отдельные элементы между собой с точки зрения их динамических свойств и, зная реакцию системы на типовые воздействия, можно судить о том, как она будет вести себя при сложных изменениях входной величины. Наиболее распространенными типовыми воздействиями являются: ступенчатое, импульсное и гармоническое воздействия.
Любой сигнал x(t), имеющий сложную форму, можно разложить на сумму типовых воздействий ui(t) и исследовать реакцию системы на каждую из составляющих, а затем, пользуясь принципом суперпозиции, получить результирующее изменение выходной величины y (t), суммируя полученные таким образом составляющие выходного сигнала yi(t). Обычно для воздействия на систему используют ступенчатый сигнал
Все остальные воздействия могут быть сведены к нему. Зависимость h(t) изменения выходной величины системы от времени при подаче на ее вход единичного ступенчатого воздействия при нулевых начальных условиях называется переходной характеристикой системы. Не менее важное значение в построении технических систем уделяется импульсной переходной характеристике ω(t), которая описывает реакцию системы на единичное импульсное воздействие при нулевых начальных условиях. Единичный импульс физически представляет из себя, ограничивающий единичную площадь, очень узкий импульс, ширина которого стремится к нулю, а высота - к бесконечности. Математически он описывается дельта - функцией d(t) = u'(t). Взяв производную от переходной функции, можно получить выражение для импульсной переходной функции ω(t) = h'(t). Переходная и импульсная переходная характеристики называются временными характеристиками системы. Каждая из них является исчерпывающей характеристикой системы и любого ее звена при нулевых начальных условиях. По ним можно однозначно определить выходную величину при произвольном входном воздействии. Еще одной важной характеристикой динамической системы является передаточная функция системы, определяющая отношение выходной величины звена y(t) к входной x(t) в каждый момент времени t:
где Передаточную функцию W(p) еще называют динамическим коэффициентом усиления.
Безынерционная (пропорциональная, усилительная) система нулевого порядка Типовое уравнение взаимосвязи выходного и входного сигналов этого звена является алгебраическим:
где k - постоянный коэффициент. Передаточная функция:
Переходная характеристика:
Пропорциональное звено мгновенно (без инерции) реагирует на возмущающее воздействие. Выходной сигнал пропорционален входному сигналу. Ордината выходного сигнала равна коэффициенту пропорциональности k. В ответ на единичное ступенчатое воздействие сигнал на выходе мгновенно достигает величины в k раз большей, чем на входе, и сохраняет это значение (рисунок 2.3.). При k = 1 звено никак себя не проявляет, а при k = - 1 - инвертирует входной сигнал.
Рисунок 2.3- Примеры безынерционного (пропорционального, усилительного) звена
Любое реальное звено обладает инерционностью, но с определенной точностью некоторые реальные звенья могут рассматриваться как безынерционные, например, жесткий механический рычаг (рисунок 4.б), редуктор (рисунок 4.2в), потенциометр (рисунок 4.г) и т.п.
Инерционное звено первого порядка (апериодическое) Звено первого порядка обладает двумя параметрами: инерционностью T и коэффициентом усиления При постоянном (единичном) входном сигнале X будет получен график, как на рисунке 3. Уравнение динамики инерционного звена первого порядка:
Передаточная функция:
Переходная характеристика имеет вид экспоненты (рисунок.2.4а), по которой можно определить передаточный коэффициент k, равный установившемуся значению h (ассимтота), и постоянную времени То по времени t, соответствующему точке пересечения касательной к кривой в начале координат с ее асимптотой.
Рисунок 2.4 – Инерционное звено первого порядка (апериодическое).
Рисунок 2.5 – Пример реализации апериодического звена при наполнении и истечении емкости с равным расходом.
Регулируемый параметр Хвых - уровень Н в баке. При «единичном скачке» Q1 уровень Н повышается, увеличивается гидростатическое давление, возрастает Q2 и затем уровень Н стабилизируется (экспонента приближается к асимптоте). Инерционные звенья второго порядка(колебательное звено) Уравнение инерционного звена второго порядка:
Передаточная функция:
Решение уравнения зависит от соотношения постоянных времени T1 и T2, которое определяет коэффициент затухания r = Можно записать
где T = T1. Если r ≥ 1, то знаменатель W(p) имеет два вещественных корня p1 и p2 и раскладывается на два сомножителя: T2p2 + 2rTp + 1 = T2 (p - p1)(p - p2). (2.14) Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.
Рисунок 2.6 – Переходная характеристика инерционного звена второго порядка: А1; А2 – амплитуда колебаний в разное время t; Тк – период колебаний; 1(t) – единичная функция; h(t) – переходная характеристика.
При r<1 корни полинома знаменателя W(p) комплексно сопряженные:
Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс (рис.2.6а), с затуханием α и частотой ω. Такое звено называется колебательным. При r = 0 колебания носят незатухающий характер. Такое звено является частным случаем колебательного звена и называется консервативным. Примерами колебательного звена могут служить пружина, имеющая успокоительное устройство (рис.2.6б), электрический колебательный контур с активным сопротивлением (рис.2.6в) и т.п. Зная характеристики реального устройства можно, определить его параметры как колебательного звена. Передаточный коэффициент k равен установившемуся значению переходной функции.
Интегрирующее (астатическое) звено Уравнение интегрирующего звена имеет следующий вид:
Передаточная функция: W(p) = k/p. (2.17) Переходная характеристика (рис.4.3.):
При k = 1 звено представляет собой “чистый” интегратор W(p) =1/p. Интегрирующее звено неограниченно "накапливает" входное воздействие. Введение его в САУ превращает систему в астатическую (рисунок 2.7а), то есть ликвидирует статическую ошибку. Примерами интегрирующих звеньев могут быть поршневой гидравлический двигатель (рис. 2.7б), электродвигатель (рис.2.7в), электрическая емкость (рис. 2.7г) и т.п.
Рисунок 2.7 – Примеры интегрирующих (астатических) звеньев.
Примером реализации астатического ТДЗ может быть любой накопитель - бак равного по высоте сечения с жидкостью, на выходе которого работает насос с постоянной производительностью (рис. 2.8).
Рисунок 2.8 – Пример реализации астатического звена – бак с жидкостью и выходным насосом.
Объекты, которые аппроксимируют астатическим или интегрирующим звеном, называют астатическими объектами.
Дифференцирующее звено Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики идеального звена:
Здесь выходная величина пропорциональна скорости изменения входной величины. Передаточная функция:
При k=1 звено осуществляет чистое дифференцирование Переходная характеристика:
Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала. Его уравнение:
Передаточная функция:
При малых Т звено можно рассматривать как идеальное дифференцирующее. Переходная характеристика имеет вид:
По переходной характеристике, имеющей вид экспоненты (рис.2.9а), можно определить передаточный коэффициент k и постоянную времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости (рис.2.9б) и демпфер, (рис.2.9в). При подаче на вход единичного ступенчатого воздействия выход оказывается ограничен по величине и растянут во времени (рис.2.9а).
Рисунок 2.9 – Разновидность типовых дифференцирующих звеньев Запаздывающее (чистого или транспортного запаздывания) звено Запаздывающее звено имеет переходную характеристику
и воспроизводит входное воздействие с запаздыванием по времени Т. Примером реализации запаздывающего звена может быть ленточный транспортёр длиной L, перемещающийся со скоростью V (рис. 2.10). Поток сыпучего материала в начале ленточного транспортёра Q1 = Хвх, поток материала, ссыпающегося в конце - Q2 = Хвых. Время движения материала по ленточному транспортёру будет равно:
Если на вход ленточного транспортёра подать возмущение типа «единичного скачка» (открыть подачу материала), то этот же «единичный скачок» появится на выходе транспортёра через отрезок времени равный времени запаздывания. Переходная характеристика запаздывающего звена изображена на рис. 2.11.
Рисунок 2-10 – Пример реализации запаздывающего звена – перемещение продукта по транспортеру.
Xвх(Τ) = Xвых(Τ + Τо). (2.27) Реальные объекты управления могут состоять из нескольких типовых звеньев ТДЗ, которые соединяются последовательно, параллельно и смешанно.
Рисунок 2.11 – Переходная характеристика запаздывающего звена.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.161.222 (0.068 с.) |
 При нулевых начальных условиях, если входной сигнал X (t=0) отсутствует, выходной сигнал Y (t=0) = 0- система находится в покое. Если подать на вход единичный сигнал, то система на выходе попытается подчиниться ему, начнет отклоняться от нулевого состояния. Ожидается, что система на выходе должна дойти до значения kx, то есть увеличить сигнал x в k раз (k — коэффициент усиления входного сигнала). Происходит это не сразу, а с некоторой задержкой, сигнал на выходе нарастает постепенно за определенное время t. Насколько замедленно реагирует система, зависит от параметра T- постоянной времени системы. Система достигнет значения y = kx на выходе и будет держать этот сигнал, пока на входе имеется единичный сигнал.
При нулевых начальных условиях, если входной сигнал X (t=0) отсутствует, выходной сигнал Y (t=0) = 0- система находится в покое. Если подать на вход единичный сигнал, то система на выходе попытается подчиниться ему, начнет отклоняться от нулевого состояния. Ожидается, что система на выходе должна дойти до значения kx, то есть увеличить сигнал x в k раз (k — коэффициент усиления входного сигнала). Происходит это не сразу, а с некоторой задержкой, сигнал на выходе нарастает постепенно за определенное время t. Насколько замедленно реагирует система, зависит от параметра T- постоянной времени системы. Система достигнет значения y = kx на выходе и будет держать этот сигнал, пока на входе имеется единичный сигнал. . (2.1)
. (2.1) (2.2)
(2.2) (2.3)
(2.3) - дифференциальный оператор, символ дифференцирования.
- дифференциальный оператор, символ дифференцирования. , (2.4)
, (2.4) . (2.5)
. (2.5) . (2.6)
. (2.6)
 .
. . (2.7)
. (2.7) . (2.8)
. (2.8) . (2.9)
. (2.9) При достаточно больших То звено на начальном участке может рассматриваться как интегрирующее, при малых Т звено приближенно можно рассматривать как безынерционное. Пример апериодического звена - четырехполюсник из сопротивления R и емкости C (рисунок 2.4б).
При достаточно больших То звено на начальном участке может рассматриваться как интегрирующее, при малых Т звено приближенно можно рассматривать как безынерционное. Пример апериодического звена - четырехполюсник из сопротивления R и емкости C (рисунок 2.4б). Еще одним примером реализации апериодического звена может быть установка - емкость равного по высоте сечения, которая изображена на рисунке 2.5. Бак на входе заполняет поток воды с расходом Q1, из бака вытекает свободно поток с расходом Q2.
Еще одним примером реализации апериодического звена может быть установка - емкость равного по высоте сечения, которая изображена на рисунке 2.5. Бак на входе заполняет поток воды с расходом Q1, из бака вытекает свободно поток с расходом Q2. (2.10)
(2.10) . (2.11)
. (2.11) . (2.12)
. (2.12) , (2.13)
, (2.13)
 (2.15)
(2.15)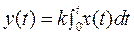 . (2.16)
. (2.16) .(2.18)
.(2.18)

 u. (2.19)
u. (2.19) . (2.20)
. (2.20)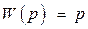 .
. (2.21)
(2.21) (2.22)
(2.22) . (2.23)
. (2.23) . (2.24)
. (2.24)
 (2.25)
(2.25) (2.26)
(2.26) Теперь представим, что на вход транспортёра подан «единичный импульс»- единица материала. Через время запаздывания мы его получим на выходе - в конце ленточного транспортёра. То же будет и с изменением входного потока по синусоиде или другому закону изменения во времени.
Теперь представим, что на вход транспортёра подан «единичный импульс»- единица материала. Через время запаздывания мы его получим на выходе - в конце ленточного транспортёра. То же будет и с изменением входного потока по синусоиде или другому закону изменения во времени. Следовательно, выходной сигнал запаздывающего звена повторяет входной сигнал, но позже на время запаздывания. Исходя из этого, можно записать общее уравнение взаимосвязи входного и выходного сигналов запаздывающего звена в динамическом режиме работы:
Следовательно, выходной сигнал запаздывающего звена повторяет входной сигнал, но позже на время запаздывания. Исходя из этого, можно записать общее уравнение взаимосвязи входного и выходного сигналов запаздывающего звена в динамическом режиме работы:


