
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аппроксимация данных регрессионными зависимостями
Одномерная линейная регрессия Регрессионные модели относятся к аналитическим моделям, получаемым в процессе исследования объекта. Часто бывает удобно представить исследуемый объект в виде серого или черного ящика, имеющего входы и выходы, не рассматривая детально его внутренней структуры. Регрессионный анализ основывается на трех математических составляющих: - методе аппроксимации; - плане эксперимента; - статистической оценке. Регрессия- это некоторая функция, построенная по экспериментальным данным и проходящая по средней траектории среди них. Регрессионный анализ основывается на методе наименьших квадратов (МНК). Парной регрессией называется уравнение связи двух переменных у и х вида
где у – зависимая переменная (результативный признак, выходная переменная); х – независимая, входная, объясняющая переменная (признак-фактор). Различают линейные и нелинейные регрессии. Линейная регрессия описывается уравнением:
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ входных переменных (объясняющие переменные), но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Примеры регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам: - полиномы разных степеней
- равносторонняя гипербола
Примеры регрессий, нелинейных по оцениваемым параметрам: - степенная
-показательная
-экспоненциальная
Построение уравнения регрессии Постановка задачи. По имеющимся данным n наблюдений (например, за производством молока и энергопотреблением животноводческой фермы x и y){(xi, yi), i=1,2,...,n} необходимо определить аналитическую (теоретическую) зависимость ŷ =f(x), наилучшим образом описывающую данные наблюдений. Построение уравнения регрессии осуществляется в два этапа (предполагает решение двух задач): – спецификация модели (определение вида аналитической зависимости)
– оценка параметров выбранной модели. Спецификация модели Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Применяется три основных метода выбора вида аналитической зависимости:
– графический (на основе анализа поля корреляций); – аналитический, т. е. исходя из теории изучаемой взаимосвязи; – экспериментальный, т. е. путем сравнения величины остаточной дисперсии D ост или средней ошибки аппроксимации A, рассчитанных для различных моделей регрессии. Оценка параметров модели Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.
В случае линейной регрессии параметры а и b находятся из следующей системы нормальных уравнений метода МНК:
Коэффициент b при факторной переменной x имеет следующую интерпретацию: он показывает, на сколько изменится в среднем величина y при изменении фактора x на 1 единицу измерения. Гиперболическая регрессия имеет вид и параметры a0 и a1:
Путем подстановки
уравнение (1.2) можно преобразовать к линейному виду:
Тогда параметры принимают вид:
Экспоненциальная регрессия:
Параметры экспоненциальной регрессии можно просчитать по формулам:
Появление знака логарифма обусловлено необходимостью линеаризации. Степенная функция:
Параметры степенной функции расчитываются по формулам:
Показательная функция:
Параметры показательной функции расчитываются по формулам:
.Логарифмическая функция:
Параметры логарифмической функции расчитываются по формулам:
Парабола второго порядка:
Парабола второго порядка имеет 3 параметра a 0, a 1, a 2, которые определяются из системы трех уравнений:
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации r2xy (для линейной регрессии) или индекс детерминации R 2 = ρ 2 xy (для нелинейной регрессии). Для оценки качества построенной модели регрессии можно использовать показатель (коэффициент, индекс) детерминации R 2 либо среднюю ошибку аппроксимации. Чем выше показатель детерминации или чем ниже средняя ошибка аппроксимации, тем лучше модель описывает исходные данные.
Средняя ошибка аппроксимации – среднее относительное отклонение расчетных значений от фактических
Построенное уравнение регрессии считается удовлетворительным, если значение Оценка значимости уравнения регрессии, его коэффициентов, коэффициента детерминации Оценка значимости уравнения регрессии в целом осуществляется с помощью F -критерия Фишера. По его значению осуществляется проверка гипотезы Но о статистической незначимости уравнения регрессии. Для этого выполняется сравнение фактического F факт и критического (табличного) F табл значений F- критерия Фишера. F факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы
где n – число единиц совокупности; m – число параметров при переменных. Для линейной регрессии m = 1. Для нелинейной регрессии вместо r 2 xy используется R 2. F табл – максимально возможное значение критерия под влиянием случайных факторов при степенях свободы k1 = m, k2 = n – m – 1 (для линейной регрессии m = 1) и уровне значимости α. Уровень значимости α – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно величина α принимается равной 0,05 или 0,01. Если F табл < F факт, то Но -гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F табл > F факт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии. Для оценки статистической значимости коэффициентов линейной регрессии и линейного коэффициента парной корреляции xy r применяется t- критерий Стьюдента и рассчитываются доверительные интервалы каждого из показателей. Согласно t- критерию выдвигается гипотеза Но о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия t факт для оцениваемых коэффициентов регрессии и коэффициента корреляции xy r путем сопоставления их значений с величиной стандартной ошибки
Стандартные ошибки параметров линейной регрессии и коэффициента кореляции определяются по формулам Сравнивая фактическое и критическое (табличное) значения t- статистики t табл и t факт принимают или отвергают гипотезу Но. t табл – максимально возможное значение критерия под влиянием случайных факторов при данной степени свободы k = n– 2 и уровне значимости α. Связь между F- критерием Фишера (при k 1 = 1; m =1) и t- критерием Стьюдента выражается равенством
Если t табл < t факт, то гипотеза Но отклоняется, т. е. a, b и rxy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t табл > t факт, то гипотеза Но не отклоняется и признается случайная природа формирования а, b или rxy. Значимость коэффициента детерминации R 2 (индекса корреляции) определяется с помощью F- критерия Фишера. Фактическое значение критерия F факт определяется по формуле
F табл определяется из таблицы при степенях свободы k 1 = 1, k 2 = n –2 и при заданном уровне значимости α. Если F табл < F факт, то признается статистическая значимость коэффициента детерминации. В формуле (3.56) величина m означает число параметров при переменных в соответствующем уравнении регрессии.
Расчет доверительных интервалов Рассчитанные значения показателей (коэффициенты a, b, rxy) являются приближенными, полученными на основе имеющихся выборочных данных. Для оценки того, насколько точные значения показателей могут отличаться от рассчитанных, осуществляется построение доверительных интервалов. Доверительные интервалы определяют пределы, в которых лежат точные значения определяемых показателей с заданной степенью уверенности, соответствующей заданному уровню значимости α. Для расчета доверительных интервалов для параметров a и b уравнения линейной регрессии определяем предельную ошибку Δ для каждого показателя:
Величина t табл представляет собой табличное значение t- критерия Стьюдента под влиянием случайных факторов при степени свободы k = n –2 и заданном уровне значимости α. Формулы для расчета доверительных интервалов имеют следующий вид:
Точечный и интервальный прогноз по уравнению линейной регрессии
Точечный прогноз заключается в получении прогнозного значения уp, которое определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения x p
Интервальный прогноз заключается в построении доверительного интервала прогноза, т. е. нижней и верхней границ уpmin, уpmax интервала, содержащего точную величину для прогнозного значения ŷp (у pmin,y< у pmax). Доверительный интервал всегда определяется с заданной вероятностью (степенью уверенности), соответствующей принятому значению уровня значимости α. Предварительно вычисляется стандартная ошибка прогноза, и затем строится доверительный интервал прогноза, т. е. определяются нижняя и верхняя границы интервала прогноза
где
Приведем пример одномерной регрессии. Пусть перед нами стоит задача определить, как количество потребляемой электроэнергии зависит от производства молока на животноводческой ферме. Результаты наблюдений отобразим на графике (см. рисунок 3.7). Всего на графике n= 24 экспериментальных точек Yiэ, которые соответствуют n наблюдениям – в каждом месяце по одному. Выдвижение гипотезы о структуре модели Рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно (рисунок 3.7), тогда гипотеза имеет вид:
Это одномерная регрессионная модель.
Рисунок 3.7- Графический вид уравнения регрессии потребления электроэнергии от производства молока Y=A0+ A1*X.
Определение неизвестных коэффициентов b0 и b1 одномерной линейной модели Для каждой из n снятых экспериментально точек вычислим ошибку (Ei) между экспериментальным значением (Yi э) и теоретическим значением (Yi Т), лежащим на гипотетической прямой b 1 X + b 0 (см. рисунок 3.8):
Ошибки необходимо сложить для всех исходных экспериментальных данных, тогда они будут характеризовать степень их приближения к теоритическим. Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку F:
Суммарная ошибка F должна быть минимальной за счет подбора коэффициентов b 0, b 1 линейной функции Y = b 1 X + b 0, чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Поэтому данный метод называется методом наименьших квадратов, который для линейной функции имеет вид:
Суммарная ошибка F, являясь функцией двух переменных b 0 и b 1, может принимать минимальное значение. Чтобы суммарную ошибку минимизировать, найходят частные производные от функции F по каждой переменной и приравнивают их к нулю (условие экстремума), в результате получают решение этой системы имеет вид:
Проверка правильности принятия линейной гипотезы о структуре модели Чтобы определить, принимается гипотеза или нет, нужно рассчитать ошибку между точками заданной экспериментальной и полученной теоретической зависимости и суммарную ошибку, а также необходимо найти значение среднеквадратической ошибки σ по формуле
где F — суммарная ошибка, n — общее число экспериментальных точек. Определим доверительный интервал S через среднеквадратическую ошибку σ:
На рисунке 3.8 приведены доверительные интервалы для представленноых на рисунке 3.7 данных по потреблению электроэнергии при производстве молока, аппроксимированных линейным уравнением Y=b0+ b1*X. Верхний Ymax и нижний Ymin доверительные интервалы
Если в зону, ограниченную линиями Y Т – S и Y Т + S (рисунок 3.8), попадает 68.26% и более экспериментальных точек Yi Э, то выдвинутая нами гипотеза об аппроксимации данных линейной зависимостью принадлежности принимается. В противном случае выбирают более сложную гипотезу или проверяют исходные данные. Если требуется большая уверенность в результате, то используют дополнительное условие: в зону, ограниченную линиями Y Т – 2 S и Y Т + 2 S, должны попасть 95.44% и более экспериментальных точек Yi Э. При увеличении доверительного интервала S зона доверительного интервала растет и растет вероятность того, что экспериментальная точка попадет в него, а это значит, что уравнения (3.69) адекватно описывают эти экспериментьальные данные.
Рисунок 3.8- Исследование допустимости принятия гипотезы о линейности модели
Условие принятия гипотезы выведено из нормального закона распределения случайных ошибок.
Линейные многомерные регрессионные модели Предположим, что функциональная структура модели с количеством входных переменных m имеет линейный вид:
Пусть в процессе эксперимента мы получаем данные о всех X1…Xm входах и выходе Y черного ящика. Тогда можно вычислить ошибку между экспериментальным (Yi Эксп.) и теоретическим (Yi Теор.) значением Y для каждой i -ой точки с повторностью n:
Минимизируем суммарную ошибку F:
Ошибка F зависит от выбора параметров b 0, b 1, …, bm. Для нахождения экстремума необходимо приравнять все частные производные F по неизвестным b 0, b 1, …, bm к нулю:
Полученная система из m + 1 уравнения с m + 1 неизвестными, которую следует решить, содержит коэффициенты линейной множественной модели b 0, b 1, …, bm. Для нахождения коэффициентов методом Крамера систему можно представить в матричном виде:
Далее, по аналогии с одномерной моделью, для каждой точки вычисляется ошибка Ei, затем находится суммарная ошибка F и значения σ и S с целью определить, принимается ли выдвинутая гипотеза о линейности многомерной модели или нет.
Точечный и интервальный прогноз по уравнению линейной регрессии Точечный прогноз - это получение прогнозного значения уp, которое определяется путем подстановки в уравнение регрессии
соответствующего (прогнозного) значения xp
Интервальный прогноз предполагает построение доверительного интервала прогноза- его нижней и верхней границ уpmin, уpmax, содержащего точную величину для прогнозного значения ŷ p (ypmin < ŷp < ŷpmax). Доверительный интервал определяется с заданной вероятностью, соответствующей принятому значению уровня значимости α. Предварительно вычисляется стандартная ошибка прогноза m ŷ p
где Далее строится доверительный интервал прогноза, т. е. определяются нижняя
и верхняя
границы интервала прогноза, где
Множественная регрессия и корреляция
Общие положения Множественная регрессия – это математическая модель, имеющая несколько входных факторов и некоторые из них необходимо учитывать. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, и их совместное воздействие на моделируемый показатель. Множественная регрессия – уравнение связи с несколькими независимыми переменными:
где у – зависимая переменная (результативный признак); Постановка задачи множественной регрессии. По имеющимся данным n наблюдений за совместным изменением n +1 параметра y и xj и ((yi, xj,i); (j = 1, 2,..., p; i = 1, 2,..., n) необходимо определить аналитическую зависимость При нахождении уравнения множественной регрессии осуществляют спецификацию модели и оценку ее параметров. Спецификация модели включает в себя решение двух задач: – отбор p факторов xj, наиболее влияющих на величину y; – выбор вида уравнения регрессии Отбор факторов при построении множественной регрессии Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого показателя (выход модели) с входными факторами модели, описывающие те или иные явления моделируемого объекта (процесса). Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели эффективности работы оборудования, например, трактора, задается его класс по силе тяги); 2. Факторы не должны быть взаимно коррелированы и тем более находиться в точной функциональной связи. Если между факторами существует высокая корреляция, то нельзя определить их влияние на результативный показатель в отдельности, и параметры уравнения регрессии оказываются не интерпретируемыми. Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации R 2, который фиксиру ет долю объясненной вариации моделируемого показателя за счет этих факторов. Влияние других, не учтенных в модели, факторов оценивается как 1 – R 2 с соответствующей остаточной дисперсией S 2. При дополнительном включении в регрессию фактора х p+1 , значимо влияющего на моделируемый показатель, коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться, т. е.
Если данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор хp +1 не улучшает модель и практически является лишним фактором. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t- критерию Стьюдента. Отбор факторов производится на основе качественного теоретико-смыслового анализа и обычно осуществляется в две стадии: – на первой подбираются факторы исходя из сущности проблемы; – на второй – на основе матрицы показателей корреляции определяют t- статистики для параметров регрессии. Коэффициенты корреляции между входными факторами позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарные, т. е. находятся между собой в линейной зависимости, если В использовании аппарата множественной регрессии возникают трудности при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой зависимостью, т. е. имеет место совокупное воздействие факторов друг на друга. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее модель регрессии. Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных:
с Через коэффициенты множественной детерминации можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение коэффициента множественной детерминации к единице, тем сильнее проявляется мультиколлинеарность факторов. Сравнивая между собой коэффициенты множественной детерминации факторов
можно выделить переменные, ответственные за мультиколлинеарность и оставить в уравнении набор факторов с минимальной величиной коэффициента множественной детерминации. Для преодоления сильной межфакторной корреляции можно использовать ряд приемов: – исключение из модели одного или нескольких факторов; – преобразование факторов, при котором уменьшается корреляция между ними. Например, переходят от исходных переменных к их линейным комбинациям, не коррелированным друг с другом (метод главных компонент). При построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней
где t- время, шаг, интервал и т.п., чтобы исключить влияние тенденции (тренда); – переход к совмещенным уравнениям регрессии, т. е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если
то возможно построение следующего совмещенного уравнения:
Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Часть этих взаимодействий могут оказаться не существенными. Поэтому необходимо провести анализ совмещенного уравнения на значимость взаимодействия факторов х1 и x 2, х1 и x 3, х2 и x 3. После исключения коллинеарных факторов осуществляется процедура отбора факторов, наиболее влияющих на изменение выхода модели (факторов, включаемых в регрессию) на основе показателей корреляции. Выбор формы уравнения регрессии Возможны линейные и нелинейные виды уравнений множественной регрессии. Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В уравнении линейной множественной регрессии
параметры bi при хi называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне. Параметр а не подлежит строгой смысловой интерпретации, однако, при всех значениях хi = 0, он указывает на некоторую величину, которая может быть базовой. В уравнении степенной функции
коэффициенты bj являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 % при неизменности действия других факторов. Для построения уравнения множественной регрессии помимо линейной и степенной чаще всего используются следующие функции: экспонента –
гипербола –
Следует иметь в виду, чем сложнее функция, тем менее интерпретируемы ее параметры. Если один и тот же фактор вводится в регрессию в разных степенях, то каждая степень рассматривается как самостоятельный фактор. Поскольку, как отмечалось, должно выполняться соотношение между числом параметров и числом наблюдений, для полинома второй степени требуется не менее 30-35 наблюдений.
Оценка параметров уравнения множественной регрессии Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений регрессии (и нелинейных уравнений, приводимых к линейным) строится система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии. В случае линейной множественной регрессии
для определения значимости факторов и повышения точности результата используется уравнение множественной регрессии в стандартизованном масштабе
где
для которых среднее значение равно нулю
а среднее квадратическое отклонение равно единице
Величины β i называются стандартизованными коэффициентами регрессии. К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (β -коэффициенты) определяются из следующей системы уравнений:
Стандартизованные коэффициенты регрессии показывают, на сколько В парной зависимости стандартизованный коэффициент регрессии β есть не что иное, как линейный коэффициент корреляции ryx. Связь коэффициентов множественной регрессии bi со стандартизованными коэффициентами βi описывается соотношением
Параметр b0 определяется из соотношения
Частные уравнения регрессии На основе линейного уравнения множественной регрессии
могут быть найдены частные уравнения регрессии, т. е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором хi при закреплении других факторов на среднем уровне. Частные уравнения регрессии имеют следующий вид:
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т. е. имеем
где
В отличие от парной регрессии, частные уравнения регрессии характеризуют частичное изменение результата моделирования от только одного варьируемого фактора, так как при этом другие факторы неизменны. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии.
Множественная корреляция Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, т.е. оценивает тесноту совместного влияния факторов на результат. Показатель множественной корреляции может быть найден как индекс множественной корреляции
где
Индекс множественной корреляции изменяется от 0 до 1. Чем он ближе к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции больше или равна максимального парного индекса корреляции
При правильном включении факторов в регрессионный анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Отсюда ясно, что, сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора. Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или совокупного коэффициента корреляции. Низкое значение коэффициента (индекса) множественной корреляции означает, что в регрессионную модель не включены существенные факторы –с одной стороны, а с другой стороны – рассматриваемая форма связи не отражает реальные соотношения между переменными. В этом случае требуются дальнейшие исследования по улучшению качества модели и увеличению ее практической значимости.
Частная корреляция
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 1236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.12.240 (0.173 с.) |
 ,
, . (3.28)
. (3.28) ; (3.29)
; (3.29) . (3.30)
. (3.30) ; (3.31)
; (3.31) ; (3.32)
; (3.32) . (3.33)
. (3.33) ;
; . (3.34)
. (3.34) , (3.35)
, (3.35)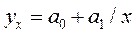 .(3.37)
.(3.37)
 (3.38)
(3.38)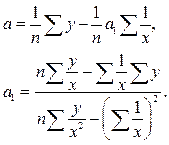 (3.39)
(3.39) (3.40)
(3.40) (3.41)
(3.41) (3.42)
(3.42) (3.43)
(3.43) (3.44)
(3.44) (3.45)
(3.45)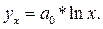 (3.46)
(3.46) (3.47)
(3.47) (3.48)
(3.48) (3.50)
(3.50) (3.51)
(3.51) не превышает 10–12 %.
не превышает 10–12 %. , (3.52)
, (3.52)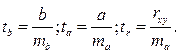 (3.53)
(3.53) (3,54)
(3,54) (3.55)
(3.55) . (3.56)
. (3.56) . (3.57)
. (3.57) (3.58)
(3.58) . (3.59)
. (3.59) .(3.60)
.(3.60) (3.61)
(3.61) ;
; (3.62)
(3.62) . (3.63)
. (3.63)
 (3.64)
(3.64) (3.65)
(3.65) (3.65а)
(3.65а) (3.66)
(3.66)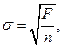 (3.67)
(3.67) (3.68)
(3.68) (3.69)
(3.69)
 (3.70)
(3.70) (3.71)
(3.71) (3.72)
(3.72)
 (3.73)
(3.73)

 (3.74)
(3.74)
 (3.75a)
(3.75a) (3.75б)
(3.75б)
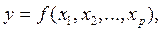 (3.76)
(3.76) – независимые переменные (факторы).
– независимые переменные (факторы). наилучшим образом описывающую данные наблюдений.
наилучшим образом описывающую данные наблюдений.
 и
и  (3.77)
(3.77) Если факторы явно коллинеарны, то они дублируют друг друга и один из них следует исключить из модели. Оставить при этом необходимо тот фактор, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.
Если факторы явно коллинеарны, то они дублируют друг друга и один из них следует исключить из модели. Оставить при этом необходимо тот фактор, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга. между факторами. В случае трех факторов определитель имеет вид
между факторами. В случае трех факторов определитель имеет вид (3.78)
(3.78) Для этого рассчитывают распределение
Для этого рассчитывают распределение  для величины
для величины (3.79)
(3.79) степенями свободы. Если фактическое значение
степенями свободы. Если фактическое значение 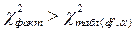 , то гипотеза H0 отклоняется. Это означает, что
, то гипотеза H0 отклоняется. Это означает, что 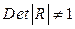 и мультиколлинеарность считается доказанной.
и мультиколлинеарность считается доказанной.
 , (3.80)
, (3.80) ,
, (3.81)
(3.81)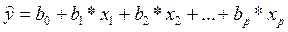 (3.82)
(3.82) (3.83)
(3.83) ,(3.85)
,(3.85) .(3.86)
.(3.86) (3.87)
(3.87) (3.88)
(3.88) -стандартизованные переменные
-стандартизованные переменные


 (3.88)
(3.88) (средних квадратических отклонений) изменится в среднем результат, если соответствующий фактор хi изменится на одну
(средних квадратических отклонений) изменится в среднем результат, если соответствующий фактор хi изменится на одну  (3.89)
(3.89) (3.90)
(3.90)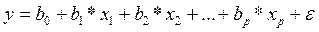
 (3.91)
(3.91) (3.92)
(3.92) (3.93)
(3.93) (3.94)
(3.94) - общая дисперсия результативного признака;
- общая дисперсия результативного признака;  - остаточная дисперсия для уравнения
- остаточная дисперсия для уравнения 
 (3.95)
(3.95) (3.96)
(3.96)


