Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностное моделирование. Метод Монте-Карло для дискретного распределения вероятностей.
Если некоторые входные или базисные переменные объекта моделирования носят случайный характер, то помимо стандартных задач анализа, целью моделирования является определение статистических характеристик выходных характеристик объекта: плотности распределения параметров, математических ожиданий, среднеквадратических отклонений (дисперсий) и т. п., а также вероятности тех или иных событий. Наибольшее распространение получили вероятностные методы статистического анализа – аналитический и численный, основанный на применение метода Монте-Карло (метод статистических испытаний) Аналитический метод состоит в поиске аппроксимирующей функции для функции распределения: f(х)=Fi(vi,t). Этот метод обладает сравнительно невысокой точностью и значительной трудоемкостью. В методе Монте-Карло данные о моделируемых событиях вырабатываются искусственно путем использования генератора равномерно распределенной в промежутке [0,1] случайной величины xR в сочетании с интегральной функцией распределения вероятностей для исследуемого процесса. В результате использования метода получается серия частных значений случайных величин, статистическая обработка которых позволяет получить сведения о характеристиках. Чем больше реализаций случайного процесса (прогонов), тем точнее результат анализа. Так, при оценке, например, математического ожидания (МО) случайной величины, каждая новая реализация случайного процесса дает новое значение, изменяющее значение МО. После первой реализации имеется единственное значение случайной величины x1, и МО равно этому значению
После третьей реализации:
и так далее. В пределе для произвольного числа реализаций n случайного процесса имеем:
Каждое новое значение случайной величины оказывает все меньшее влияние на МО. Следовательно, с увеличением числа реализаций случайного процесса точность моделирования по МО возрастает, и в пределе, при числе реализации, стремящихся к бесконечности, МО, рассчитанное по экспериментальным модельным реализациям случайного процесса, будет стремиться к реальному МО. Если некоторое случайное событие А наступает как следствие какого-либо из nА событий при общем числе n возможных событий (несовместимых и равновероятных), то частота наступления события А при увеличении числа испытаний стремиться к вероятности:
при условии существования данного предела. В методе Монте-Карло для реализации генератора с заданной функцией распределения используют источник случайных чисел с равномерным распределением в интервале (0,1). Равномерным называют такое распределение, при котором каждое из чисел избранного интервала имеет одинаковую вероятность появления. Искусственную случайную выборку из совокупности величин, описываемой некоторой функцией распределения вероятностей, получают в следующем порядке: 1) строят график или таблицу функции распределения на основе ряда чисел, отражающего исследуемые события или процессы, откладывая по оси x значения случайной переменной, а по оси y – значения вероятностей; 2) выбирают случайное число с помощью генератора случайных чисел в пределах от 0 до 1 (с требуемым числом разрядов); 3) строят линию, параллельную оси х, от значения выбранного случайного числа до пересечения с кривой распределения вероятностей и, затем, от полученной точки линию, параллельную оси у, до пересечения с осью х, получая выборочное значение случайной величины по заданному типу распределения. 19. *Использование метода Монте-Карло для реализации неравномерных распределений. Метод Монте-Карло может быть использован для решения некоторых детерминированных задач: например, приближенного вычисления интеграла вида:
Геометрически такой интеграл равен площади фигуры, ограниченной графиком функции f (x), приведенным на рис. 11.
Распределим случайным образом точки в прямоугольнике поиска (см. рис. 11). Обозначим через N 1 количество точек, попавших в прямоугольник, и через N 2 – количество точек под кривой, т. е. попавших в заштрихованную площадь под функцией (эти точки изображены на рис. 11 закрашенными). Количество точек, попавших под кривую по отношению к общему числу точек пропорционально площади под кривой (величине интеграла) S по отношению к площади испытуемого прямоугольника:
Вычисление S будет тем более точным, чем большее число точек будет использовано.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.244.216 (0.004 с.) |
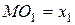 . После второй реализации МО рассчитывается как среднее двух случайных величин:
. После второй реализации МО рассчитывается как среднее двух случайных величин: .
.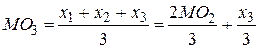 ,
, .
.