
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные методы построения интерполяционных моделейСодержание книги
Поиск на нашем сайте
Классический численно-аналитический подход заключается в том, чтобы использовать некоторые узлы функции для получения приближающего многочлена и затем выполнить аналитическую операцию над этим многочленом. Этот процесс может быть назван «аналитической заменой», так как функция, которую невозможно обработать, заменяется другой функцией, над которой уже можно выполнить аналитическую операцию. Например, в способе Ньютона для нахождения нуля функции y=f(x) дается приближенное значение х1 и вместо кривой используется прямая
которая касается графика функции в точке (x 1 у 1 ). Подставляя у = 0, получаем значение х, являющееся корнем этой новой функции,
Это новое значение х 1 используется как следующее приближенное значение корня. Поскольку с многочленами легко обращаться, большая часть классического численного анализа основывается на приближении многочленами. Однако, для многих целей предпочитаются другие классы функций. Выбрав узлы и класс приближающих функций, необходимо выбрать одну определенную функцию из этого класса посредством некоторого критерия — некоторой меры приближения или «согласия». Самый широко применяемый критерий состоит в требовании того, чтобы приближающая функция совпадала с заданными значениями в узловых точках. Другой, более общий, критерий — «наименьшие квадраты» — означает, что «сумма квадратов отклонений между данными узлами и приближающей функцией в узловых точках должна быть минимальной». Однако, иногда применяются и другие критерии. Прежде чем начать вычисления, необходимо решить также, какую точность надо иметь в ответе и какой критерий будет избран для измерения этой точности. Все изложенное можно сформулировать в виде четырех вопросов: — какие узлы будут использованы? — какой класс приближающих функций будет использован? — какой критерий согласия будет применен? — какую точность нужно получить?
2.1. Интерполяция многочленами с произвольно
Существуют два главных применения интерполяционных формул. Прежде всего, они применяются для целей замены графически заданной функции аналитической. Второе главное применение их — для интерполяции в других численных методах. Многочлен степени n,
имеет n +1 коэффициент. Естественно полагать, что n +1 условие, наложенное на многочлен в общем виде, позволит однозначно определить коэффициенты. В частности, можно потребовать, чтобы многочлен проходил через n +1 точку (xi , yi) (i= 1,2, …, n +1) с xi ,≠ xj. То, что многочлен проходит через точки (xi , yi) означает выполнение условий
Определитель для этих n +1 линейных уравнений относительно неизвестных ак есть определитель Вандермонда, который не равен нулю, если xi ,≠ xj для i ≠ j
Возвращаясь к главной задаче о нахождении многочлена по n +1 точке (xi, yi), очевидно, что ее всегда можно решить и найти коэффициенты ак по правилу Крамера или другим способом. Все изложенное можно подытожить, сказав, что если есть n + 1 узловая точка функции, то можно найти многочлен степени п, который совпадает (пренебрегая ошибками округления) с функцией в узловых точках. Предположив, что они близки, можно использовать многочлен вместо функции в дальнейших аналитических процессах: интегрировании, дифференцировании, отыскании нулей и т. д.
2.1.1. Интерполяция полиномами Лагранжа
Другой подход к задаче интерполяции — метод Лагранжа. Основная идея этого метода состоит в том, чтобы прежде всего найти многочлен, который принимает значение 1 в одной узловой точке и 0 во всех других. Легко видеть, что функция
(где i ≠ j у знака произведения означает «исключая j значение») является требуемым многочленом степени п; он равен 1, если x=xj и 0, когда x=xi, i ≠ j. Многочлен принимает значение yi в i -й узловой точке и равен нулю во всех других узлах. Из этого следует, что
есть многочлен степени п, проходящий через п + 1 точку (xi, yi). Таким образом, можно сделать следующее важное замечание: если дана п + 1 узловая точка, то соответствующий многочлен степени п, проходящий через эти точки, однозначно (в пределах ошибок округления) определен, независимо от того, как он строится и какие обозначения использованы.
2.2. Интерполяция многочленами с равноотстоящими узлами. Конечные разности
Очень часто имеющаяся информация о функции (в виде значений в узловых точках) задана на множестве равноотстоящих значений х. В этом случае большая часть формул, вычислений, как, впрочем, и затрагиваемых идей, заметно упрощается. До сих пор не делалось никаких предположений о заданных значениях аргумента, которые могли быть совершенно произвольными. Предположим дополнительно, что рассматриваемые значения аргумента являются равноотстоящими, т. е. образуют арифметическую прогрессию. Такое предположение обычно имеет место при интерполировании функций, заданных в виде таблиц с постоянным шагом, где x1 = x0+h, x2=x0+2h, xm= x0+mh. Разность h арифметической прогрессии и называется шагом таблицы. Построение интерполяционных формул в этом случае значительно упрощается. Прежде чем перейти к рассмотрению этого вопроса, вводится понятие конечных разностей. Пусть значения функции f(x) заданы в точках х0, х1 = х0 + h,..., хп = х0 + nh (узлы интерполяции). Составляются разности значений функции y1 ─ y0 = y2 ─ y1 = …………….. Yn ─ yn-1 = Эти значения называют первыми разностями функции, или разностями первого порядка. По ним можно составить разности второго порядка, или вторые разности и вообще разности любого порядка k, или k-e разности Δkym = Δk-1ym-1─ Δk-1ym (1.7) Эти последовательные разности обычно располагают в форме таблицы. Таблица конечных разностей
Пусть значения функции y=f(x ) заданы для равноотстоящих значений аргумента x0, x1=x0 + h, x2 = x0 +2 h,…, xn=x0 + nh. Значения y обозначаются соответственно y0 = f(x0), y1 = f(x1), …, yn=f(xn). Существует единственный многочлен F (х) степени п, такой, что F (xk)=yk (k = 0, 1 ,…, п ). Предлагается другой способ записи и отыскания этого многочлена, который, в конечном счете, совпадает с многочленом, полученным по формуле Лагранжа. Записывается искомый многочлен в виде
Для определения коэффициентов а0,а1,...,ап полагаем
Далее, полагая х=х1, получаем
Так как (x1 ̣─ x0)= h то
Продолжая вычисление коэффициентов, полагается
Заменим найденные коэффициенты а0, а1 их значениями
Воспользовавшись формулой, выражающей разности через значения функции, получим
Точно так же определяется
Аналогичные дальнейшие вычисления позволяют записать общую формулу для отыскания коэффициентов
Подставив найденные выражения коэффициентов в формулу 1.8, находим
Полученную формулу и называют первой интерполяцион- Теперь ясно видно различие между формулами Ньютона и Лагранжа. В формуле Лагранжа (1.4) каждое из слагаемых представляет многочлен п-й степени и все эти слагаемые равноправны. Поэтому заранее (т. е. до производства вычислений) нельзя пренебрегать какими- либо из них. В формулу же Ньютона входят в качестве слагаемых многочлены повышающихся степеней, причем коэффициентами при них служат последовательные конечные разности, деленные на факториалы. Очевидно, что последовательные разности обычно довольно быстро уменьшаются. Это положение дает возможность не учитывать в формуле Ньютона тех слагаемых, коэффициенты при которых становятся пренебрежимо малыми. Благодаря этому, можно вычислять промежуточные значения функции достаточно точно, пользуясь простыми интерполяционными формулами. Для практического пользования формулу Ньютона
Множители, входящие в формулу (2.16), выразятся через t следующим образом
Подстановка этих выражений в формулу (1.10), приводит ее квиду
Это и естьокончательный вид первой интерполяционной Первая интерполяционная формула Ньютона наиболее удобна для отыскания значений функции, соответствующих большим, нежели начальные, значениям аргумента, чем и объясняется приведенное выше ее другое название — интерполяционная формула для интерполирования вперед. Для интерполирования в конце таблицы применяется иная формула. Искомый интерполяционный многочлен представляется в форме
Используя аналогичные вычисления, общая формула для коэффициентов будет иметь вид
После подстановки в (1.13) полученных значений коэффициентов формула примет вид:
Это и есть вторая интерполяционная формула Ньютона. Для применения ее предварительно преобразуют, как и первую. Использовав замену
Формулу (1.16) называют второй интерполяционной формулой Ньютона или интерполяционной формулой Ньютона для интерполирования назад.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.255.122 (0.008 с.) |

 ,
,
 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3)
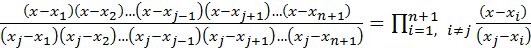 (1.4)
(1.4) (1.5)
(1.5)
 (1.6)
(1.6)
 (1.8)
(1.8)


 откуда
откуда




 (1.9)
(1.9)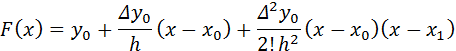
 (1.10)
(1.10)
 или x=x0 + th (1.11)
или x=x0 + th (1.11)


 (1.12)
(1.12)
 (1.13)
(1.13)
 (1.14)
(1.14) (1.15)
(1.15) или x = xn + th, интерполяционная формула окончательно примет вид
или x = xn + th, интерполяционная формула окончательно примет вид (1.16)
(1.16)



