Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторные работы №№ 1, 2, 3, 4Содержание книги Поиск на нашем сайте
Российской федерации
Государственное образовательное учреждение высшего профессионального образования (технический университет)”
Подлежит возврату № 0000 МОДЕЛИРОВАНИЕ СИСТЕМ
Лабораторные работы №№ 1, 2, 3, 4
Методические указания по выполнению лабораторных работ
Для студентов специальности 220201
МОСКВА 2011 Составители: А.В. Алешин В.В. Болдов Редактор А.В. Кочемасов
Методические указания содержат руководство для выполнения лабораторных работ по курсу "Моделирование систем". Материал предназначен для студентов 4 курса дневного отделения факультета "Кибернетика" специальности 220201 «Управление и информатика в технических системах». Методические указания содержат описание и порядок выполнения лабораторных работ, в которых изучаются методы построения и использования математических моделей при анализе и проектировании технических систем.
Печатаются по решению редакционно-издательского совета университета.
Рецензенты: М.Х. Дорри, Г.С. Колесников
©МИРЭА, 2011 Лабораторная работа №1 Применение методов интерполяции Цель работы Цель предлагаемой лабораторной работы — показать главные идеи в области вычислений и изучить методы интерполяции для построения математических моделей устройств автоматических систем. Первые работы для решения задачи моделирования обычно связаны с вычислением значений функции. Главными инструментами здесь являются «общее чутье» и «маленькие хитрости». Второе, — это интерполяция недостающих в таблице значений, например, в логарифмической или тригонометрической таблице. В процессе решения задачи интерполяции исходными данными являются несколько узлов функции и нужно вычислить приближенно некоторые значения, которых нет в таблице. В большинстве таблиц сделано предположение, что функция ведет себя между последовательно взятыми точками, как прямая, хотя в ряде случаев разумно предположить, что она ведет себя, как квадратный трехчлен и даже многочлен более высокой степени. Приемы интерполяциииспользуются для других вычислительных задач таких, как интегрирование, дифференцирование, нахождение нулей, решение дифференциальных уравнений, оптимизация, задач анализа и проектирования систем. Применение интерполяционных формул Задание на лабораторную работу Построить интерполяционные полиномы по заданным узлам, используя различные виды полиномов. Оценить точность полученной модели в зависимости от степени полинома. Оценить сложность (число умножений) решения задачи интерполяции для различных видов полиномов. Лабораторная работа №2 Моделирование тепловой подсистемы
Цель работы Целью работы является изучение принципов моделирования технических систем. В данной работе решаются задачи построения математической модели и проведение исследования на этой модели. Получение эквивалентных схем технических объектов
При получении ММ достаточно сложного технического объекта, состоящего из нескольких физических подсистем, нужно: выделить в объекте однородные физические подсистемы; получить эквивалентные схемы каждой из подсистем; установить связи между подсистемами; получить математическую модель системы. Задание на лабораторную работу Провести исследование распределения температур по поверхности объекта в стационарном режиме (теплоемкости элементов не рассматриваются) Оценить быстродействие программы анализа для различных методов вычисления температур. Выбрать элемент конструкции радиатора охлаждения процессора по критерию наименьшего перегрева процессора.
ЛАБОРАТОРНАЯ РАБОТА №2 Построение математической модели Цель работы
Целью работы является изучение методики построения математической модели по результатам натурного исследования. Основные понятия
На практике в производственных или лабораторных условиях встречаются процессы, характер протекания которых детерминированным образом зависит от определенных величин x 1, x 2, …., xn Переменные х1,. х2, …, .хп обычно называют входными контролируемыми или независимыми переменными, и их возможные значения принадлежат некоторой области n -мерного пространства. Выходная переменная y в дальнейшем будет называться зависимой переменной, целевой величиной или выходом процесса, даже если она не обозначает буквально выход продукта. В общем случае можно сказать, что между независимыми переменными и выходом процесса y существует функциональная взаимосвязь y=y (x), где x= (х1,. х2, …, .хп) T — вектор значений независимых переменных. Зависимость на практике часто бывает не известна и тогда она находится путем обработки экспериментальных данных. Так как всякий эксперимент связан с появлением случайных ошибок, то при построении математических моделей на основе экспериментальных данных необходимо использовать методы математической статистики. Наиболее часто при решении этой задачи применяют метод наименьших квадратов. Метод наименьших квадратов позволяет построить оптимальную, в определенном смысле, оценку моментов распределения ошибки эксперимента, а также решить вопрос о том, является ли полученная модель адекватной (т. е. соответствует ли она действительности). Пусть требуется на основе экспериментальных данных построить модель некоторого процесса. При этом прежде всего необходимо составить себе какое-то представление о структуре этой модели. Из физических соображений можно, например, предположить, что взаимосвязь между у и х - линейна: y (a,x) = a0 + a 1 x 1 + a 2 x 2 +…+ a n x n (2.1) При этом аi являются неизвестными параметрами процесса, оценки которых требуется найти путем обработки экспериментальных данных. В случае, если характер связи описывается нелинейной квадратичной функцией, имеем y (a,x) = a0 + a 1 x 1 + a 2 x 2 +…+ a n x n + + a 11 x 1 x 1 + a 22 x 2 x 2 +…+ a 33 x 3 x 3+…+ a nn x n x n+ + a 12 x 1 x 2 + a 12 x 1 x 2 +…+ a 13 x 1 x 3+…+ a 1n x 1 x n + + a 23 x 2 x 3+… + a n-1n x n-1 x n Здесь число неизвестных параметров определяется:
Обычно коэффициенты нелинейной квадратичной модели нумеруются не по порядку, а так, что коэффициент при функции xixj обозначается через аij Модели полиномиального вида имеют большое значение в связи с тем, что с их помощью любая аналитическая функция может быть описана как угодно точно. Однако, с увеличением степени полинома весьма существенно увеличивается число оцениваемых параметров модели и соответственно возрастают затраты на эксперимент. Так, если степень полинома есть т, то число неизвестных параметров находится по формуле:
В дальнейшем будут использованы модели вида y=y (x,a) (2.2) где a ― вектор параметров модели, a= (a 0, a 1, …, ak) T Примем, что модель (2.2) линейна относительно коэффициентов аi, т.е. y (a,x)= a 0 f 0(x) + a 1 f 1(x) +…+ akfk(x) (2.3) При этом fi (х) — известные функции, являющиеся компонентами вектора. Используя векторные обозначения можно записать y = aTf (x)= f T (x) a В случае линейной или квадратичной модели выражения для компонент f (х ) будут иметь вид: f (x)=(1, x 1, x 2, …, xn) T и f (x)=(1, x 1, x 2, …, xn, x 1 x 1, x 2 x 2, xnxn, x 1 x 2, x 1 x 3, x 1 xn, x 2 x 3,…, xn- 1 xn) T Эксперимент проводится в многомерном пространстве при условии N>k + 1где N ― число точек эксперимента, k ― число искомых параметров модели. Вектор переменных имеет вид xi =(x 1 i, x 1 i,…, xni) T, i=1, 2,…, N.
По результатам эксперимента вычисляется матрица F
и матрица C
Матрица C называется дисперсионной матрицей. Значения параметров модели ai находятся как решение системы линейных уравнений
где Y - вектор результатов эксперимента. Оценка дисперсии ошибок наблюдений вычисляется с помощью остаточной суммы квадратов
с числом степеней свободы φ = N – k ̶ 1 по формуле
Коэффициент ai - считается значимо отличающимся от нуля, если
где t кр—критическое значение распределения Стьюдента для заданного уровня значимости a и j степеней свободы (если оценка si2 имеет j степеней свободы); t крнаходится с помощью нижеприведенной таблицы из условия
Таблица для оценки значимости параметров модели
ЛАБОРАТОРНАЯ РАБОТА №4 Автоматических систем Цель работы Целями предлагаемой лабораторной работы является моделирование различных временных процессов в устройствах автоматических систем и получение практических навыков в использовании методов анализа процессов с помощью решения дифференциальных уравнений численными методами. Задание на лабораторную работу
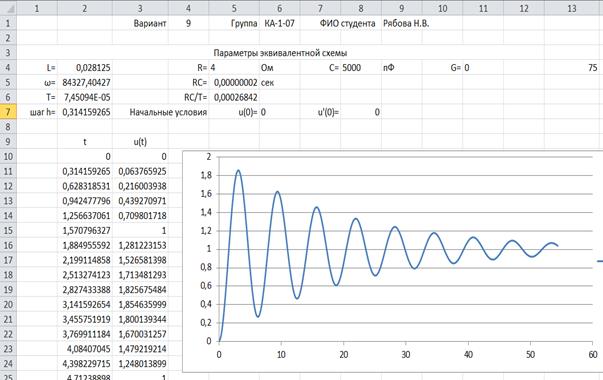
Индивидуальные варианты для выполнения лабораторной работы приведены на листе «Задания». Ввести свой номер варианта в окно «Вариант» на листе «Исходные данные» В соответствии с вариантом задания подготовить аналитическое решение дифференциального уравнения для дальнейшей оценки погрешности численных методов. Решение дифференциального уравнения (4.2) для начальных условий имеет вид:
где Вариант решения уравнения приведен на рис. 4.2.
Рис. 4.2 Аналитическое решение дифференциального уравнения
Последовательно для различных численных методов составить алгоритмы численного решения дифференциального уравнения в соответствии с формулами. Используя средства таблиц Microsoft Excel или VBA Microsoft Excel, подготовить процедуры решения. Вычислить по разработанным процедурам значения u2(t). Построить таблицы решения и графики. Сравнить результаты с аналитическим решением.
Библиографический указатель
1. Трудоношин В.А., Пивоврова Н.В. Математические модели технических объектов. М.: Высш. шк., 1986. – 160с. 2. Планирование эксперимента в исследовании технологических процессов / К. Хартман и др. – М.: Мир, 1977 –552с. 3. Хемминг Р.В. Численные методы – М.: Наука, 1972 –552с. 4. Андре Анго, Математика для электро- и радиоинженеров – М.: Наука, 1964 –772с. 5. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. – М.: Наука, 1970 –432с.
Российской федерации
Государственное образовательное учреждение высшего профессионального образования (технический университет)”
Подлежит возврату № 0000 МОДЕЛИРОВАНИЕ СИСТЕМ
Лабораторные работы №№ 1, 2, 3, 4
Методические указания по выполнению лабораторных работ
Для студентов специальности 220201
МОСКВА 2011 Составители: А.В. Алешин В.В. Болдов Редактор А.В. Кочемасов
Методические указания содержат руководство для выполнения лабораторных работ по курсу "Моделирование систем". Материал предназначен для студентов 4 курса дневного отделения факультета "Кибернетика" специальности 220201 «Управление и информатика в технических системах». Методические указания содержат описание и порядок выполнения лабораторных работ, в которых изучаются методы построения и использования математических моделей при анализе и проектировании технических систем.
Печатаются по решению редакционно-издательского совета университета.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.113.71 (0.008 с.) |



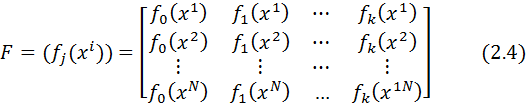
 (2.5)
(2.5) (2.6)
(2.6)
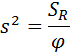


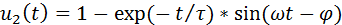 ,
,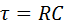 ,
,