
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння в повних диференціалахСодержание книги Поиск на нашем сайте
Рн-я 1 називають рівнянням у повних диференціалах якщо його ліва частина є повним диференціалом деякої функції Ф(х,у), яка має неперервні похідні по кожному аргументу до другого порядку включно.
Треба знайти необхідну умову, для того щоб р-ня 1 було рівнянням у повних диференціалах. Припустимо, що це так:
Оскільки похідні 2 порядку від функції Ф неперервні за умовою то вони рівні за теоремою з мат. аналізу, тому При умові викон. і побуд. потр. ф-ю
Прип. що р-ня (1) не є р-ням в повних дифер. тоді доцільно застосув. інтегральний множник Озн. Диф. ф-я
Множник
Лінійні рівняння першого порядку Озн. Р-ня
1o Метод Лагранжа(варіації довільною сталою) Розгл. одноріднетр-ня (2), яке є р-ням з відокр. змінними.
20 Метод Бернуллі Провед. заміну змін. Підст. знайд. ф-ю в ост. р-ня одерж.
Тоді
Однорідні диференціальні рівняння та рівняння, що зводяться до однорідних Озн. Ф-ю Озн. Однорідн. назив р-ня виду
Розв. р-ня: 10
20 Зробимо заміну
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

 (1).Будем вважати,що в прямокутникуП.a<=x<=b, c<=y<=d функції
(1).Будем вважати,що в прямокутникуП.a<=x<=b, c<=y<=d функції  мають непер частин похідні другого порядку.
мають непер частин похідні другого порядку. =0 =>
=0 =>  , тобто цим виразом визначається загальний інтеграл рівняння1.
, тобто цим виразом визначається загальний інтеграл рівняння1.

 - необхідна умов. існ. ф-ї
- необхідна умов. існ. ф-ї  ., що є і достатньою умовою.
., що є і достатньою умовою.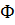 :
:  продиф. її по y.
продиф. її по y. 
 не зал. від x, це р-ня з відокр. зм., знах. один з його розв.
не зал. від x, це р-ня з відокр. зм., знах. один з його розв.  і запиш. заг. інтегр. р-ня (1).
і запиш. заг. інтегр. р-ня (1).
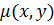 назив. інтегрув. множн. р-ня (1), якщо р-ня
назив. інтегрув. множн. р-ня (1), якщо р-ня  (2) є р-ням у повних дифер.
(2) є р-ням у повних дифер. ,
, 
 необхідно підібрати так, щоб праві частини двох рівностей були рівними. Може статися,
необхідно підібрати так, щоб праві частини двох рівностей були рівними. Може статися,  тобто
тобто  Тоді запиш р-ня у вигл
Тоді запиш р-ня у вигл  ,
, 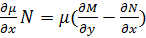 ,
,  .Зауваж,що прав частин не залеж від
.Зауваж,що прав частин не залеж від  . З остан р-ня знаходь
. З остан р-ня знаходь  тоді
тоді  – не зал від x. і
– не зал від x. і 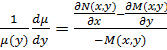 .Одерж р-ня є р-ням в повн дифер,яке ми вміємо розв.
.Одерж р-ня є р-ням в повн дифер,яке ми вміємо розв. , (1) де a(x), b(x) неперервні на(a,b), b(x)≠0 назив. неоднор. лін. р-нями 1-го порядку. у випадку b(x)=0 р-ня назив. однорідн.
, (1) де a(x), b(x) неперервні на(a,b), b(x)≠0 назив. неоднор. лін. р-нями 1-го порядку. у випадку b(x)=0 р-ня назив. однорідн.  (2).
(2).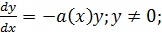


 с1 є R. Шукаємо розв’язок 1 у вигляді
с1 є R. Шукаємо розв’язок 1 у вигляді  (*) будем вваж, що c є невідомою ф-єю, задача полягаэ в тому щоб знай. знач. індек. так, щоб вир. (*)став розв. р-ня (1).
(*) будем вваж, що c є невідомою ф-єю, задача полягаэ в тому щоб знай. знач. індек. так, щоб вир. (*)став розв. р-ня (1). 

 Отже,
Отже, 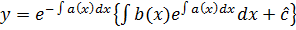 є загал розв неоднор р-ня.
є загал розв неоднор р-ня. де
де  невідомі дифер. ф-ї на
невідомі дифер. ф-ї на  Підставимо в р-ня (1)
Підставимо в р-ня (1)  Згрупуємо 1 та 3 дщоданки
Згрупуємо 1 та 3 дщоданки  Обер. за ф-ю
Обер. за ф-ю 
 частк. розв. р-ня
частк. розв. р-ня  . Оберемо з цих розв’язків
. Оберемо з цих розв’язків 



 називають однорідною ф-єю мулевого степення, якщо для
називають однорідною ф-єю мулевого степення, якщо для  справдж. рівність
справдж. рівність 
 якщо ф-я
якщо ф-я 
 ; введ. заміну змінної
; введ. заміну змінної  , де - х≠0.
, де - х≠0.  ; одерж. р-ня є р-ням з відокр. змін.
; одерж. р-ня є р-ням з відокр. змін. 
 ;
; 


 - дійсні числа
- дійсні числа здійснимо заміну змінної
здійснимо заміну змінної ; тоді
; тоді 
 Одерж. Сист р-нь,. така с-ма має єдин. розв. якщо її детермінант відмінний від 0. знаход. розв. с-ми (4) і підстав. його в заміну (3). тоді р-ня (2) набув. виду
Одерж. Сист р-нь,. така с-ма має єдин. розв. якщо її детермінант відмінний від 0. знаход. розв. с-ми (4) і підстав. його в заміну (3). тоді р-ня (2) набув. виду  одерж. р-ня є однорідн.
одерж. р-ня є однорідн. його розв.
його розв.

 - з відокр. змінними.
- з відокр. змінними. ;
;  його розв.
його розв.


