
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составление логических функций.Содержание книги
Поиск на нашем сайте
Логическая функция может быть записана аналитически различными сочетаниями операций сложения и умножения переменных. Однако с точки зрения представления логической функции и последующего синтеза логической схемы наиболее удобны формы записи, при которых функция выражается либо в виде суммы произведений переменных, либо в виде произведения их сумм. Запись логической функции в виде суммы произведений переменных называют дизъюнктивной нормальной формой (ДНФ):
а запись функции в виде произведения сумм — конъюнктивной нормальной формой (КНФ):
Инверсия любой функции, записанной в дизъюнктивной (конъюнктивной) нормальной форме, по правилу (1.5) дает замену записи на конъюнктивную (дизъюнктивную) нормальную форму. Например, инверсия функции
имеет вид
Логическую функцию, заданную любым аналитическим выражением, можно преобразовать к ДНФ или КНФ, пользуясь правилами алгебры логики. Для каждой логической функции может существовать несколько равносильных дизъюнктивных и конъюнктивных форм. Вместе с тем имеется только один вид ДНФ и КНФ, в которых функция может быть записана единственным образом (совершенные нормальные формы). В совершенной дизъюнктивной нормальной форме (СДНФ) каждое входящее слагаемое включает все переменные (с инверсиями и без них) и нет одинаковых слагаемых. В совершенной конъюнктивной нормальной форме (СКНФ) каждый входящий сомножитель включает все переменные (с инверсиями и без них) и нет одинаковых сомножителей. Логическая функция наиболее наглядно и полно представляется так называемой таблицей соответствия или истинности, в которой для каждой комбинации значений переменных указывается значение функции. Таким образом, таблица истинности определяет алгоритм работы создаваемой цифровой схемы. От табличного представления функции переходят к аналитической записи ее в СДНФ или СКНФ. Пусть в качестве примера функция F задана в виде табл.2.3. Для комбинаций переменных 2, 7, 8 функция F истинна (т. е. F=1), что означает для указанных комбинаций равенство единице следующих произведений: хуz=1. Таблица 2.3 Таблица истинности
Комбинации переменных, при которых функция истинна, называют конституентами единицы или минтермами. Представление логической функции в виде суммы минтермов определяет ее СДНФ, т. е. в данном случае: Функция, определяемая таблицей истинности, может быть представлена не только ее единичными, но и нулевыми значениями. Так, на основании табл.2.3 рассматриваемая функция ложна (F =0 или F=1), если истинно каждое из произведений
Воспользовавшись законом инверсии, приходим к записи функции в СКНФ:
Каждый сомножитель в этом соотношении состоит из суммы переменных, для которых функция обращается в нуль в соответствии с таблицей истинности. Такие суммы называют конституентами нуля или макстермами. Таким образом, произведение макстермов определяет СКНФ функции.
Примеры составления логических функций. Простую логическую функцию иногда можно записать в аналитической форме непосредственно из словесного определения. Покажем это на примере составления функций «Равнозначность» и «Неравнозначность», которые будем использовать в дальнейшем. Функция «Равнозначность» принимает значение 1, если две ее входные переменные имеют одинаковые логические потенциалы: x1=x2=1 ИЛИ x1=x2=0. Поэтому ее представляют как Функция «Неравнозначность» принимает значение 1, если две ее входные переменные имеют разные логические потенциалы: x1=1, x2=0 ИЛИ x1=0, x2=1. Поэтому ее представляют в следующем виде:
где значок
Рис.2.3 Условные изображения элементов «Равнозначность» (а) и «Неравнозначность» (б).
Функцию «Неравнозначность» иначе называют «Исключающее ИЛИ». Ей присуще интересное свойство: если на один ее вход подать лог.1, то логический потенциал, поданный на второй вход, будет на выходе инвертирован; если же вместо лог.1 на один вход подать лог.0, то функция будет вести себя как повторитель логического потенциала, поданного на другой вход. Это легко проверит это самостоятельно. Условное изображение элемента «Неравнозначность» дано на рис. 2.3,б. Вместо приведенного значка (=1) используется значок m2, указывающий на то, что «Исключающее ИЛИ» функционирует по правилам сложения одноразрядных двоичных чисел (сложение по модулю 2): 1+0=1; 0+1=1; 0+0=0; 1+1=0 (при арифметическом сложении единица переносится в соседний более старший разряд). В общем случае для получения аналитической формы функции используют таблицы истинности. Пример 2.8. Пусть на выходе некоторого устройства должен появиться сигнал высокого уровня (лог.1, у=1), если на входах устройства действует комбинация сигналов х1х2х3 из набора №1 ИЛИ из набора №2 ИЛИ из набора №3 ИЛИ из набора №6, приведенные в табл.2.4. Если на каждом перечисленном наборе конъюнкция сигналов будет равна лог.1, то на выходе устройства будет сигнал высокого уровня (U1). Таким образом, функция, представленная табл.2.4, запишется в виде где сигналы х1,х2,х3, инвертированы, если они в соответствующих наборах равны лог.0 (иначе конъюнкция не будет равна 1). Таблица 2.4 Таблица истинности функции y
Такая форма логической функции, как указывалось ранее, называется совершенной дизъюнктивной нормальной формой ( СДНФ). Она представляется логической суммой простых конъюнкций, каждая из которых содержит все переменные в прямом или инверсном виде не более одного раза; в такие конъюнкции не входят суммы переменных, а также отрицания произведений двух или более переменных. Входящие в СДНФ конъюнкции называются минтермами или конституентами единиц. Логическая сумма конъюнкций, отличающаяся от (2.9) тем, что все конъюнкции или некоторые из них не содержат всех переменных (в прямом или инверсном виде), представляет собой дизъюнктивную нормальную форму (ДНФ) функции. Логическую функцию можно составить не только по единичным, но и по нулевым значениям. Из табл.2.4 следует, что на наборах №№0, 4, 5, 7 у =0. Чтобы на каждом указанном наборе имело место у=0, нулю должна равняться дизъюнкция переменных из этого Набора, т.е. каждое слагаемое дизъюнкции; если в данном наборе переменная равна единице, то в дизъюнкцию должна входить ее инверсия. На всех указанных наборах функция из табл.2.4 будет равна 0, если осуществить конъюнкцию составленных дизъюнкций:
Здесь у =0 обеспечивают: первый сомножитель при Форма, в которой выражена функция (2.10), называется совершенной конъюнктивной нормальной формой (СКНФ). Она представляется логическим произведением дизъюнкций, каждая из которых содержит все переменные в прямом или инверсном виде не более одного раза. Дизъюнкции, входящие в произведение сомножителей, называются макстермами или конституентами нулей. Логическое произведение дизъюнкций, отличающееся от (2.10) тем, что все дизъюнкции или некоторые из них не содержат всех переменных (в прямом или инверсном виде), представляет собой конъюнктивную нормальную форму (КНФ) функции. Так как одна и та же логическая функция, выраженная определенной таблицей истинности, записывается в СДНФ и СКНФ, то каждую из этих форм можно преобразовать в другую. Логическая функция имеет единственные СДНФ и СКНФ, что непосредственно следует из методики их построения.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.221 (0.007 с.) |

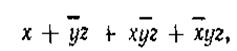


 .
. .
.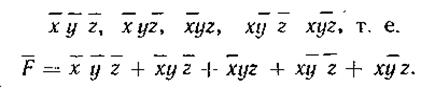

 . Условное изображение элемента «Равнозначность» приведено на рис.2.3,а.
. Условное изображение элемента «Равнозначность» приведено на рис.2.3,а. ,
,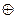 - символизирует функцию «Неравнозначность».
- символизирует функцию «Неравнозначность».
 , (2.9)
, (2.9) . (2.10)
. (2.10) (при х3=x2=х1=1, т. е. на наборе № 0), второй сомножитель при
(при х3=x2=х1=1, т. е. на наборе № 0), второй сомножитель при  (при х3=0; x2=х1=1, т. е. на наборе № 4), третий сомножитель при
(при х3=0; x2=х1=1, т. е. на наборе № 4), третий сомножитель при  (при х3=х1=0; х2 =1, т. е. на наборе № 5), четвертый сомножитель при х3=х2=х1=0, т.е. на наборе № 7.
(при х3=х1=0; х2 =1, т. е. на наборе № 5), четвертый сомножитель при х3=х2=х1=0, т.е. на наборе № 7.


