
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кількість переставлень обчислюють за формулоюСодержание книги Поиск на нашем сайте
Pm=m! (28) Приклад застосування. Задача. На полиці розташовано 10 книжок (різних). Скільки існує варіан- тів їх розташування? Розв’язок. P10=10!=3628800 Зауважимо, що переставлення є взаємно однозначне відображення множини на себе.
5.7 Комбінації або сполучення Підмножина потужності n у множині з потужністю m є конфігу- рація з назвою “комбінація” або “сполучення”. Кількість таких конфігура-
Підмножина так само, як і розміщення, не має повторень елементів, Кількість кортежів-розміщень перевершує кількість підмножин за рахунок переставлень елементів кортежа, яких маємо n!. Звідси кількість
перевіримо формулу для множини S={a,b,c,d}, якщо потужність підмно- жини n=2. Є такі варіанти підмножин: {a,b}, {a,c}, {a,d}, {b,c}, {b,d},
{c,d}. Формула дає кількість варіантів - 6.
Приклад застосування. Задача. Під час передачі двійкових даних 8-розрядна кодова комбінація може мати зміни у деяких розрядах (або помилки) внаслідок дії перешкод. Якщо помилки відбулися у двох розрядах, то це двократна помилка. Скільки існує варіантів двократної помилки? Розв’язок. Надамо номери розрядам кодової комбінації. Множина номерів розрядів А={1,3,2,4,5,7,8,6} має потужність |A|=8. Кожен варіант дворазо- вої помилки можна описати як підмножину потужності 2 у множині A. Наприклад, підмножина {3,1} може означати, що помилки відбулися у розрядах з номерами 3 та 1. Тоді для m=8 та n=2 всього існує 28 варіантів
дворазових помилок, бо
5.8 Властивості формули для обчислення кількості комбінацій
Важливо також, що
(30) Цей вираз є основа для побудови трикутника Паскаля:
..................... У трикутнику Паскаля: - два сусідні елементи будь-якого рядка у сумі дають елемент, розта- шований між ними, але нижче на рядок, - кожен рядок містить коефіцієнти складових у формулі бінома Ньютона відповідного степеня, - якщо від вершини трикутника торувати шлях до будь-якого елемен-та трикутника, роблячи кроки від елемента до сусіднього елемента тільки униз, то кількість можливих шляхів дорівнюватиме числовому значенню елемента.
Трикутник у числовому варіанті виглядає наступним чином. 1 1 1 2 1 1 3 3 1 1 4 6 4 1 .................... Можна перевірити, що сума елементів рядка є число 2, піднесене до степеня, що є номер рядка, починаючи з нульового номера рядка вершини трикутника.
5.9 Комбінації з повтореннями Такі конфігурації не є кортежі і не є підмножини. Не кортежі, бо порядок розташування елементів значення не має. Не підмножини, бо є повторення елементів. Конфігурації визначені кількістю елементів (m) та потужністю множини (n), елементи якої використовують (копіюють) для побудови конфігурації. Приклади конфігурацій для m=6 та множині A={a,b,c,d}, n=|A|=4: [a,a,c,a,b,b], [d,d,d,d,d,d], [c,a,c,a,c,b]
Кількість конфігурацій позначають як Вираз для обчислення кількості конфігурацій можна вивести з наступних міркувань. Оскільки порядок розташування елементів у конфі- гурації значення не має, розташуємо елементи груповано у порядку їх запису у множині для наведених прикладів: [a,a,a,b,b,c], [d,d,d,d,d,d], [a,a,b,c,c,c] Характер елементів значення не має, тому у конфігураціях можна позначати їх однаково (хай буде позначка “0”), залишаючи лише позначки меж, де закінчується один різновид елементів і починається інший: [0,0,0,1,0,0,1,0,1], [1,1,1,000000], [0,0,1,0,1,0,0,0,1] Конфігурації, зображені у такий спосіб, є взаємно однозначне відобра- ження прикладів конфігурацій, запропонованих раніше. Виходить, що конфігурації відрізняються лише розташуванням меж (одиниць у двійко- вому числі, у якому кількість одиниць дорівнює n-1, а кількість роз- рядів дорівнює m+n-1). Задачу з розташуванням двох одиниць у 8-роз- рядному двійковому числі (двократні помилки) ми розглянули у розділі
Нями
(31) Приклад застосування. Задача. Маємо три гральні кістки (гральна кістка – кубічної форми, на кожній грані кількістю крапок позначено число. Числа – 1, 2, 3, 4, 5, 6. Три гральні кістки водночас кидають на стіл - три числа на верхній грані кісток складають конфігурацію. Скільки існує таких конфігурацій? Розв’язок. Кількість елементів у конфігурації m=3, розташування елементів у конфігурації значення не має; потужність множини, з еле-ментів якої побудовано конфігурації n=6; за всіма ознаками ці конфігу-рації є комбінації з повтореннями, тому
5.10 Переставлення з повтореннями та поліноміальні коефіцієнти
Поліном на відміну від бінома має у доданках більш ніж два спів- множника окрім коефіцієнтів, бо є результатом обчислення виразу
(32)
Результат обчислення можна вважати сумою кортежів довжини n, серед яких є еквівалентні, бо (для n=7)
Еквівалентні кортежі утворюються шляхом переставлення елементів, тому це переставлення з наявністю повторень елементів у кортежі. Кількість еквівалентних складових дорівнює поліноміальному коефіцієнту. Для кожного віріанта доданку буде свій коєфіцієнт. Знайдемо вираз для обчислення поліноміальних коефіцієнтів.
вано на a місцях складатиме. Для кожного такого варіанту з решти місць (у кількості n-a) на частині місць у кількості b буде розташовано елемент y. Кількість варіантів такого розташування дорівнюватиме кіль- комбінацій з n-a по b, що дає загальну кількість варіантів у відповідно-
сті з виразом Зауважимо, що сума показників степеня у знаменнику, тобто, a+b+(n-a-b) дорівнює n. Аналогічно у загальному випадку, якщо відомі степені всіх співмножників конкретного доданку з виразу (32), поліноміальний коефіцієнт для цього доданку обчислюють за виразом
, (33)
де Приклад застосування. Залача. Який буде поліноміальний коефіціент для доданку, що містить
Розв’язок.
Ще задача. Скільки буде варіантів розбиття множини потужності n=9 на три підмножини, якщо у першій підмножині - 2 елементи, у другій підмножині - 4 елементи, у третій підмножині - 3 елементи? Розв’язок. Припустимо, що є кортеж довжини 9, у якому місця мають номери від 1 до 9. Номери місць у кортежі складають множину потуж-ності n=9. Будь-який кортеж довжини 9, у якому дворазово присутній елемент x, триразово присутній елемент z та чотириразово елемент y, є розбиття множини номерів місць у кортежі на підмножини, де перша підмножина місць містить x, друга підмножина місць містить y і третя підмножина місць містить z. Кількість варіантів такого розбит-тя дорівнює кількості переставлень з повтореннями або поліноміально- му коефіцієнту з попередньої задачи, їх буде 1260.
5.11 Як розпізнати конфігурацію.
Наведені приклади використання формул для визначення кількості конфігурацій призначені допомогти читачеві розібратись в якій ситуації мають місце ті чи інші конфігурації, та з чого випливає, яку саме формулу слід використати. Але досвід показує, що цього не достатньо. Тому нижче запропоновано алгоритм, за яким можна провести аналіз і одержати від- повідь на запитання - до якої з розглянутих класичних конфігурацій належить та, що є у вашій задачі. (Зрозуміло, що конкретна задача не обо- в’язково закінчується розпізнаванням конфігурації та використанням від- повідної формули). Ви маєте підрахувати кількість якихось конфігурацій …
Якщо ви міняєте місцями елементи у конфігурації,
чи буде то
вже інша конфігурація серед та ж сама конфігурація серед тих, які вам треба підраху- тих, які вам треба підраху- вати? вати?
Чи є повторення елементів Рис.5-1 у складі конфігуруції?
Конфігурація Конфігурація Конфігурація не є кортеж є кортеж є підмножина і не є підмножина
Конфігурація Конфігурація Конфігурація не є кортеж є кортеж є підмножина і не є підмножина
Якщо потужність Конфігурації мають назву
Чи є повто - однакова, конфі- повтореннями ”. рення елемен- гурації мають наз- тів у кортежі? ву “ комбінації ”.
ні так
Чи однакова кількість Чи є обмеження елементів у кортежі та на кількість однако - у множині, з елемен- вих елементів у тів якої побудовано складі кортежа
так ні Конфігурації
Конфігурації Конфігурації “ переставлення мають назву мають назву з повтореннями “, “ переставлення ” “ розміщення ” кількість є поліно - Міальний коефіцієнт
Конфігурації мають назву “ розміщення з повтореннями “ Рис.5-1 (продовження) або “ вибірки ”.
6 Групи. Застосування у кодах.
6.1 Визначення Група – алгебраїчна система з однією визначальною операцією. Загальний запис
де A – множина, °- позначка операції (тут абстрактної) над елементами множини. Відносно операції та множини є низка вимог:
1) результат операції над елементами множини має належати цій множині; кажуть – множина є замкнена відносно операції; якщо ця ви- мога виконана, алгебраїчна система має назву – групоїд; 2) операція має бути асоціативною; якщо ця вимога виконується разом з вимогою п.1, алгебраїчна система має назву – півгрупа; 3) множині має належати нейтральний елемент для операції (позначимо літерою “е”), такий, що
якщо ця вимога виконується разом з вимогами п.1 та п.2, алгебраїчна система має назву – моноїд; 4) для кожного елемента множини у складі множини має бути обернений елемент, такий, що
та; обернений елемент для цих виразів не обов’язково один і той же. Якщо виконані всі чотири умови – алгебраїчна система є група.
6.2.1 Група переставлень або симетрична група порядку n!. Порядок групи дорівнює потужності множини групи. Припустимо n=3, потужність множини n!=3!=6. Слово “переставлення” тут слід розу-
міти не як кортеж з трьох елементів, у якому переставлено місцями еле-менти, а як алгоритм-вказівку про те, як саме здійснити одноразове переставлення. Такий алгоритм зображують двома рядками. Верхній ря- док показує розташування елементів до переставлення, нижній – після пе- реставлення, наприклад:
А=
переставлень продукує третє, еквівалентне за дією послідовному вико-нанню двох, наприклад:
(34)
Операція виконана за таким правилом. У першому стовпчику пер- шого переставлення маємо перехід a®b. Стовпчик другого переставлен-
ня, що має верхній елемент b, має перехід b®c. З двох переходів маємо ланцюжок a®b®b®c, у якому початковий та кінцевий елементи ство-рюють стовпчик з переходом a®c, тобто, перший стовпчик переставлен- ня - результата операції. Аналогічно ланцюжок b®c®c®b дає другий стовпчик з переходом b®b і ланцюжок c®a®a®a дає третій стовпчик результата з переходом c®a.
відає вимогам. 1) вимога замкненості множини відносно операції виконана; це ви- пливає з таких міркувань: результат операції над двома переставленнями є теж переставлення; множина A містить у собі всі можливі варіанти пере-ставлень і тому містить у собі результат операції; 2) вимога асоціативності операції виконана, бо для будь-яких трьох елементів множини A можна довести можливість переставлення дужок так, як це показано у наступному прикладі:
,
після виконання операцій у дужках маємо:
і далі;
3) множині A належить елемент, який є нейтральний,
бо або, тобто вимога
наявности нейтрального елемента у множині - виконана; 4) вимога наявності оберненого елемента для кожного у множині виконана бо можна запропонувати наступний спосіб одержання обернено-го елемента для кожного елемента множини A: у елемента треба переста- вити місцями рядки, потим переставити місцями стовпчики, щоб верх-
для елемента одержимо обернений і
елементи групи не обов’язково числа і операції не обов’язково арифметич- ні.
6.2.2 Zn– група остач (залишків) за модулем n
Ця алгебраїчна система складається з множини залишків від ділен-
залишає від числа у дужках залишок від його ділення на n. Доведемо, що
1) операція дає результат - залишок від ділення на n, а мно- жина B містить всі варіанти залишків від ділення на n, тому результат опе- рації завжди належить множині і замкненість гарантована; 2) асоціативність операції випливає з того, що під час виконання
операції спочатку виконують звічайне додавання, а воно асоціативне; 3) у складі множини є нейтральний елемент; це 0; складання з нулем дає у результаті другий операнд операції; 4) обернений елемент для кожного елемента множини групи можна
,
Таким чином Znє група.
6.2.3 Коди у остачових (залишкових) класах
Ідея кодування цілих додатних чисел шляхом використання замість чисел залишків від їх ділення на відповідні модулі приваблює тим, що під час додавання чисел (як у групі Zn) немає перенесень у старші розря- ди, а це відкриває можливість принаймні одержати підвищену щвидкість функціонування лічильників з регістрацією чисел та суматорів у спеціалі- зованих обчислювальних пристроях. Залишкові класи – це підмножини цілих додатних чисел, поєднані відношенням еквівалентності; числа екві- валентні за тією ознакою, що мають однаковий залишок під час ділення на певне число. Розглянемо приклад, що демонструє можливість додавання багаторозрядних чисел без перенесень. Трирозрядні числа будуватимемо, розташовуючи у першому (зліва) розряді елементи групи Z7, у другому розряді елементи групи Z9, у третьому - Z8. Діапазон чисел, які можна зобразити таким кодуванням дорівнює 7×9×8=504, тобто можна цим кодом зобразити десяткові числа від 0 до 503. Процедура кодування поля- гає в одержанні залишків за відповідним модулем. Десяткове число 100
виглядатиме як 412, бо 100mod8=4, 100mod9=1, 100mod7=2. Розглянемо додавання чисел 109 та 156: Десяткові Кодовані запропонованим кодом числа числа за модулями 8 9 7 109 à 5 1 4 + Å 156 à 4 3 2 ________________________ 1 4 6 ß результат додавання за результат à 265 à 1 4 6 модулями 8,9,7 десяткового додавання Таким чином, можливі операції додавання багаторозрядних чисел без перенесень з використанням кодування у залишкових класах
6.2.3 Група коренів рівняння xn=1
має ще один дійсний корінь x=-1, якщо n парне. Інші корені (всього їх має бути n) комплексні з модулем 1. Множина коренів з операцією мно-
рівняння x5=1. Впевнитись, що ком- плексні числа є корені равняння, можна піднесенням кореня до степеня 5; результат дорівнюватиме 1. Наприклад,
Перевіримо, що система відповідає вимогам до груп: 1) добуток, якщо співмножники є корені з множини A, теж нале-
(35)
чень змінної i, а це дасть ціле число від 0 до 4 включно, тобто, один з коренів; 2) aсоціативність операції звичайного множення доведення не потре-бує;
3) для операції множення у складі множини A є нейтральний еле- мент; це 1; 4) для кожного кореня з певним значенням змінної i можна запро-понувати корінь із значенням змінної 5-i, який є обернений елемент до нього та їх добуток дорівнюватиме нейтральному елементу, тобто 1. Таким чином, система U5є група.
6.2.5 Група n-розрядних двійкових чисел з операцією підсумовування розрялами (XOR)
Алгебраїчна система G=(C, XOR) для n=3 має множину С={000,001,011,010,100,101,110,111). Операція XOR є у складі команд будь-якої ЕОМ і виконується складанням без перенесень у старший розряд. Покажемо виконання вимог групи: 1) підсумовування розрядами двох елементів множини С дасть трирозрядне двійкове число, а множина C містить всі варіанти таких чи- сел, тому результат операції обов’язково належить множині C і замкне- ність множини відносно операції гарантована; 2) під час виконання операції XOR кожен розряд обробляється окремо шляхом підсумовування за модулем 2, а ця операція була ви- знана асоціативною у прикладі груп залишків за модулем, тому опера- ція XOR асоціативна; 3) у складі множини С є нейтральний елемент 000; 4) кожний елемент групи є обернений сам до себе, оскільки під- сумовування розрядами двох однакових чисел дає нульовий результат, тобто, нейтральний елемент. Таким чином, алгебраїчна система G=(C, XOR) є група.
6.2.6 Група многочленів над GF(2)
Многочлени над GF(2) мають складові з паднесеної до різного степеня (але не більше n) формальної змінної x з коефіцієнтами з поля Галуа характеристики 2. Поле тут це алгебраїчна система з двома виз-начальними операціями; це додавання за модулем 2 та множення. Якщо характеристика дорівнює 2, множина аклгебраїчної системи складається з двох елементів {0,1}. Це значить, що коефіцієнти складових або оди-ниці, або складові відсутні; під час додавання многочленів коефіцієнти підсумовуються за модулем 2, як і в операції поля GF(2). Розглянемо приклад для n=3. Алгебраїчна система Мn=(D,Å) є група. Визначимо, що є множина і як виконується операція. Множина
(36)
Переглянемо виконання вимог до групи: 1) операція така, що поява у доданків показників степеня, відмінних від 0,1,2,3 неможлива; всі варіанти многочленів є у складі множини D, тому результет операції завжди буде належати множині D і замкненість гарантована; 2) під час обчислення коефіцієнтів многочлена використовують опера-цію додавання за модулем, яка є асоціативною (розділ 6.2.2), тому опера- ція додавання многочленів теж є асоціативною; 3) нейтральний елемент 0 належить множині D; 4) для кожного елемента множини D у складі множини D можна знай- ти обернений, бо кожний елемент є обернений сам собі. Таким чином, алгебраїчна система Мn=(D,Å) є група.
6.3 Підгрупи
пи. Розглянемо приклад. У групі залишків за модулем, де A={0,1,2,3.4.5}, виділимо підмножину D. DÌA, D={0,3}. Перевіримо
1) множина має всього 2 елементи, тому неважко віконати всі мож- ливі операції в системі і впевнитись, що результат операції завжди нале-
кнекність множини відносно операції; 2) асоціативність у операції є, бо операцію не змінювали; 3) нейтральний елемент у групі та підгрупі той же самий – 0;
теж виконана. Таким чином, система є підгрупа у групі.
6.4 Циклічна підгрупа
Розглянемо спосіб виділити підгрупу у групі. Нехай маємо деяку
Візьмемо елемент множини qÎQ і будемо виконувати багаторазово групову операцію, щоб одержати
доти, поки не отримаєимо qm=e (нейтральний елемент). Тоді з множиною F={q,q2,q3,…qm} система (F,°) є циклічна підгрупа. Доведемо, що вимо-
ги групи тут виконані. Якщо перемножити два елементи з множини F,
(37) можна стверджувати, що у показниках степеня відбуваються такі ж дії, як у групі Zm. Для доведення виконання вимог групи цього достатньо з посиланням на ізоморфізм груп (подібність алгебраїчних систем розгля-немо нижче). Приклад. Задача. Знайти циклічну підгрупу у групі Z12, бе- ручі q=4. Розв’язок: q=4, q Å12q=8, q Å12q Å12q=12mod12=0 Звідси G=(B, Å12), де B={4,8,0}, є підгрупа порядку 3 у множині Z12. Порядок підгрупи (або групи) є потужність множини підгрупи (абогрупи). Порядок елемента групи є порядок циклічної підгрупи, яку виділено за допомогою цього елемента.
6.5 Теорема Лагранжа
Теорема Лагранжа встановлює звязок між порядком групи та можли- вими варіантами порядку підгруп у цій групі. Формулювання її таке: порядок елемента групи ( порядок підгрупи ) є дільником порядка групи. Це означає, що, коли, наприклад, у групі 12 елементів, то можли- ві підгрупи з 1, 2, 3, 4, 6, 12 елементів. А якщо у групі 7 елементів, то можуть бути лише тривіальні підгрупи (вони є завжди) з одного та з семи елементів. У цьому випадку (коли порядок групи є просте число) нама- гання виділити циклічну підгрупу призведе до виділення всієї групи. Це іноді використовують для пошуку розв’язків рівнянь, відносно яких відо- мо, що розв’язки створюють групу. Маючи один з розв’язків, виділенням циклічної підгрупи знаходять інші розв’язки. Наприклад, знаємо, що коре- ні алгебраїчного рівняння x7=1 створюють групу відносно множення. Коренів всього 7. Один корінь x=1 – дійсне число, інші - комплексні числа. достатньо знайти хоча б один комплексний корінь – багаторазовим мно- женням можна знайти всі інші комплексні корені. Нехай знаємо один ком-плексний корінь
.
6.6 Розбиття групи на суміжні класи
Суміжні класи це специфічні підмножини групи, які не мають взаєм- них перетинів і мають однакові потужності з підгрупою, використаною для розбиття. Якщо виконати групову операцію між елементом групи, який не належить підгрупі, та всіма елементами підгрупи, то одержимо
підмножину групи з такою властивістю: виконання групової операції між будь-яким елементом цієї підмножини і множиною підгрупи виділить знову цю ж підмножину групи (суміжний клас). Для виділення наступного суміжного класу треба виконати групову операцію між елементом групи, що не належить ні підгрупі, ні вже виділеній підмножині групи (суміжно-
мо також підгрупу у цій групі, де HÌA, A={a1,a2,a3,…,am}; якщо aiÏH, операція ai°H віділить суміжний клас H1= ai°H, якщо ajÏH та ajÏH1, то операція aj°H віділить наступний суміжний клас H2= aj°H і так далі, поки не будуть виявлені всі n суміжних класів (n=½A½¤½H½). Приклад: Розбиття групи Z12= (A, Å12) на суміжні класи за підгрупою B=(H, Å12), де A={0,1,2,3,4,5,6,7,8,9,10,11}, H={4,8,0}. Суміжний клас, якщо виберем елемент 3ÏH, H1= 3 Å12H= 3 Å12{4,8.0}={7,11,3}; наступ- ний суміжний клас з елементом 5ÏH, H2= 5 Å12H= 5 Å12{4,8.0}={9,1,5}; і нарешті з елементом 2, який не належить ні підмножині, ні жодному з виділених суміжних класів, маємо H3= 2 Å12H= 2 Å12{4,8.0}={6,10,2}. Таким чином, маємо розбиття A=HÈH1ÈH2ÈH3, бо HÇH1=Æ, HÇH2=Æ, HÇH3=Æ, H1ÇH2=Æ, H1ÇH3=Æ, H2ÇH3=Æ.
7 Подібність алгебраїчних систем
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.213.201 (0.013 с.) |

 цій позначають
цій позначають
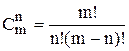 комбінацій без повторень
комбінацій без повторень

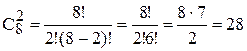
 Це такі властивості:
Це такі властивості:







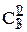




 5.7, скориставшись аналогією, маємо кількість комбінацій з повторен-
5.7, скориставшись аналогією, маємо кількість комбінацій з повторен-
 m елементів
m елементів
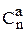 Припустимо, що треба знайти кількість еквівалентних доданків у (32), у складі яких є множник xayb(степені інших складових нас не цікавлять). Кількість варіантів кортежів довжини n, у яких x розташо-
Припустимо, що треба знайти кількість еквівалентних доданків у (32), у складі яких є множник xayb(степені інших складових нас не цікавлять). Кількість варіантів кортежів довжини n, у яких x розташо-



 при обчисленні?
при обчисленні?










 ні так
ні так





 всіх підмножин “ комбінації з
всіх підмножин “ комбінації з



 кортеж?
кортеж?
 так ні
так ні


 мають назву
мають назву

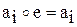
 ;;
;;

 6.2 Приклади груп
6.2 Приклади груп
 Тому загальний запис групи складається з множини перестав-
Тому загальний запис групи складається з множини перестав- лень
лень та з операції композиції переставлень з позначкою “ ”. Операція з двох
та з операції композиції переставлень з позначкою “ ”. Операція з двох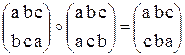
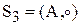 Проаналізуємо, чи є система групою, тобто, чи відпо-
Проаналізуємо, чи є система групою, тобто, чи відпо-



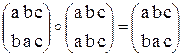


 доведемо, що це обернений елемент:
доведемо, що це обернений елемент: ня цілих додатних чисел на n та операції складання за модулем n, тобто,
ня цілих додатних чисел на n та операції складання за модулем n, тобто, , B=(0,1,2,…,n-1),. Операція modn
, B=(0,1,2,…,n-1),. Операція modn
 є група.
є група. обчислити за виразом
обчислити за виразом бо
бо Рівняння має один дійсний корінь x=1, якщо n непарне,
Рівняння має один дійсний корінь x=1, якщо n непарне, ження створюють групу, тобто, система, де A – множина ко-
ження створюють групу, тобто, система, де A – множина ко- ренів, є група. Підтвердимо це на прикладі для n=5. Множина коренів
ренів, є група. Підтвердимо це на прикладі для n=5. Множина коренів
 жить множині A; це тому, що
жить множині A; це тому, що і під час множення маємо складати показники степеня, що зводиться пі-сля винесення за дужки до складання за модулем 5 двох зна-
і під час множення маємо складати показники степеня, що зводиться пі-сля винесення за дужки до складання за модулем 5 двох зна-
 Результат пояснюється тим, що
Результат пояснюється тим, що

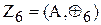 Підгрупа це підмножина групи, яка відповідає всім вимогам гру-
Підгрупа це підмножина групи, яка відповідає всім вимогам гру-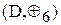 виконання вимог до групи у алгебраїчній системі:
виконання вимог до групи у алгебраїчній системі:

 жить множині D:,.; наявна зам-
жить множині D:,.; наявна зам-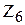

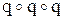

 q, (умовно позначимо, як q), (позначимо, як q) і так
q, (умовно позначимо, як q), (позначимо, як q) і так
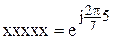

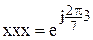

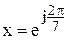
 , тоді інші,,,,
, тоді інші,,,,
 му класу), та множиною підгрупи. Тобто, маємо групу, має-
му класу), та множиною підгрупи. Тобто, маємо групу, має-


