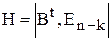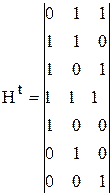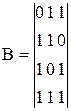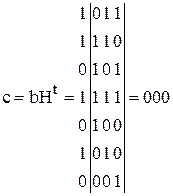Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ступіні та умови подібності систем
Під час розгляду прикладів груп була помітна схожість групи залиш-ків за модулем та групи коренів рівняння xn=1 або групи двійкових чи-сел з операцією XOR та групи многочленів над GF(2). Цілком доречне питання – за яких умов подібність є достатньою підставою для поширення результатів вивчення однієї алгебраїчної системи на іншу і коли таке мож-ливе також у зворотному напрямку.
та
існує відображення Г множини A на множину B (Г:A®B) таке, що
тезу, але для бінарної операції, пояснює рисунок 7-1. Якщо водночас існує гомоморфізм K на M та гомоморфізм M на K, то такий ступінь
подібності має назву і зоморфізм. Якщо використовується відображення множини на її підмножину то ступінь подібності має назву ендоморфізм.
Рис.7-1 Ілюстрація до умов наявності гомоморфізма алгебраїчної системи K на систему M.
7.2 Приклади
x6=1. Маємо алгебраїчні системи:
відображення множини A на множину B подане за допомогою двочаст- кового графа нижче (рис.7-2).
Рис. 7-2 Відображення A®B
Перевірка відповідності операндів та операцій полягає у наступному. 1) нейтральний елемент Z6відображено у нейтральний елемент К 2) операція між будь-яким елементом та нейтральним у Z6дає у
результаті вихідний елемент і це ж відбувається з їх образами у K, бо
множення на 1 залишає результат. 3) операція між будь-якими двома елементами у Z6та її результат чітко відповідають операціям над образами елементів і образ результата, який одержано у Z6, завжди дорівнює результату операції над образами операндів у системі K.
Приклад ізоморфізму між півгрупою додатних дійсних чисел та півгрупою дійсних чисел. Маємо системи: A=(R+,×) та B=(R,+) R+ - множина додатних R - множина дійсних дійсних чисел чисел
У цих систем кількість та арність операцій однакова. Результати відображення множини R+ ® R, якщо xÎR+, yÎR, дістають за виразом y=lg x; відображення множини R ® R+ - за виразом x=10y. Відповідність операндів та результатів відома, бо то є підстава для використання звичайних десяткових логарифмів, які добре полегшують виконання операцій множення та піднесення до степеня.
Приклад ендоморфізму групи трирозрядних двійкових чисел з операцією XOR G=(C, XOR), С={000,001,011,010,100,101,110,111) на підгрупу G1=(D,XOR), D={000,111}. Зрозуміло, що кількість і арність операцій у групи та підгрупи не мо- жуть бути різними. Відображення множини C на множину D1 можливе за таким правилом: якщо елемент у складі множини C має у молодшому розряді одиницю, то образ цього елемента у множині D1 є 111, інакше образ елемента є 000. Перевірки (невичерпні) не суперечать наявності автоморфізму: 011 ® 111 011 ® 111 101 ® 111 XOR XOR XOR 100 ® 000 010 ® 000 111 ® 111 ___ ___ ___ ___ ___ ___
111 ® 111 001 ® 111 010 ® 000
Взаємно-однозначна відповідність простору функцій на інтервалі аргументів та простору багавтовимірних векторів була основою для побу- дови функціонального аналізу (розділ математики). Кільця. Ідеали кілець. Це алгебраїчні системи з двома визначальними операціями. Першу з них умовно звуть складанням, другу множенням. Загальний запис R=(A,+,×). Щоб система була кільцем потрібно виконання наступних вимог: 1) множина та операція складання мають створювати комутативну групу (операція має бути ще й комутативна); 2) замкненість множини відносно множення; 3) асоціативність множення 4) дистрибутивність множення відносно складання Якщо система відповідає цим вимогам, то вона має назву - асоціативне кільце. Додатково - якщо операція множення комутативна, то система має назву - комутативне кільце; - якщо у множині є нейтральний елемент за множенням, то система
- якщо для елементів множини A можливо, то система має назву - кільце з дільниками нуля, а ці елементи є дільники нуля. Приклад: R=(A,Å6,Ä6), A={0,1,2,3,4,5), операція множення за мо- дулем 6 виконується аналогічно додаванню за модулем, тобто, після зви-
чайного множення знаходять залишок від ділення результата звичайного множення на 6. Перевіримо виконання вимог: 1) є комутативна група за складанням за модулем 6; операція ко- мутативна; 2) результат операції множення за модулем обов’язково належить множині A, тобто замкненість множини відносно операції множення гарантована; 3) асоціативність множення можна стверджувати на підставі того, що під час виконання операції спочатку виконують звичайне множення, а воно асоціативне та комутативне; 4) дистрибутивність можна перевірити за виразом
Таким чином, маємо комутативне кільце. До складу множини належить нейтральний елемент за множенням (це 1), а також 2Ä63=0. Це комутативне кільце з одиницею з дільниками нуля. Ідеал кільця це підмножина кільця, яка є підгрупа за складаннам,
що містить в собі всі добутки елементів кільця (перший операнд) та підмножини кільця (другий операнд). У попередньому прикладі група за додаванням має підгрупу з множиною I={0,2,4}. Ця підмножина кіль-ця має властивість: якщо її помножити за модулем 6 на будь-який еле- мент кільця, то результатом буде або повторення множини, або число, яке належить підмножині. Така підмножина і має назву - ідеал кільця. Важ- лива властивість ідеала - у ньому завжди є елемент, на який можна поділити без залишку всі елементи ідеала. У прикладі це 2. 9 Елементи теорії похибкостійкого кодування.[9]
9.1 Проблема достовірності передачи даних та деякі її розв’язки
Розглядатимемо бінарні лінії зв’язку, сигнали у яких на протязі так- тового інтервалу інтерпретують як 0 або 1. Повідомлення у таких лініях виглядають як послідовності на зразок - 10111010001 та таке інше. Через електричні перешкоди на приймальному кінці можливе спотворен- ня послідовності. Завдання теорії похибкостійкого кодування полягає у розробці такої системи передавання інформації, у якій можлива швидкість передавання залишається ще високою, а можливість (віроємність) помилок стає порів- няно невелика. Серед заходів задля зменшення кількості помилок є багаторазове передавання. Кожна кодова комбініція може бути n разів (n – непарне) повторена під час передачи, а на приймальному кінці мажоритарною об- робкою кожного розряду готують одну кодову комбінацію для отримувача. Мажоритарна обробка – це вироблення рішення відносно того, що саме було передано у конкретному розряді повідомлення шляхом визначення, чого було більше у цьому розряді у всіх повтореннях повідомлення - нулів чи одиниць. Такий захід діє добре, але це втрата швидкості переда- вання у n разів! Коли частота помилок невелика така втрата невиправда- на. Теорія стверджує, що зовсім необов’язково передавати так багато пов- торень. Більш доцільно до блоку даних, що призначений для передавання, додати деяку килькість надлишкових бітів (іноді байтів), які послугову-ватимуть для виявлення або до того ж ще і для виправлення помилок.
який треба передати, ставить у відповідність вектор
випадку вектори можна ототожнити з двійковими числами. Тобто, буде-мо писати a =1001110…10, b =1001111…00. Перешкоди діють,
змінюючи деякі розряди і замість вектора (або кодової комбінації) b
на приймальному кінці лінії матимемо b`. Якщо виконати операцію b XOR b` = e, результат матиме одиниці лише у розрядах, де відбулися зміни, і має назву - вектор помилки. Тому модель виникнення помилок під час передавання повідомлень лінією для нас полягатиме у операції b` = b XOR e, або b` = b Å e (позначка Å замість XOR для зручності).
9.2 Алгебра кодування лінійним кодом
Розглянемо n-вимірний лінійний арифметичний простір над полем GF(2). Вектори у цьому просторі це різноманітні двійкові n-розрядні
(n,k) звуть лінійний k-вимірний підпростір в (поле Галуа ха- рактеристики 2n). Тут n-довжина кодових комбінацій, k- кількість інфор- маційних розрядів у кодових комбінаціях. Назва “лінійний” пояснюється тим, що кожна кодова комбінація побудована, як вектор, з ортів, помножених на коефіцієнти-компоненти. Тобто, вектор - лінійна комбінація ортів. Оскільки підсумовування компо- нент під час операцій відбувається за модулем 2, сума двох кодових ком- бінацій є також кодова комбінація з цього підпростору або з цієї підгрупи. Задати конкретний лінійний код (n,k) можна за допомогою пород- жуючої матриці. Структура матриці:
(38) E4– квадратна одинична матриця, Bk,(n-k)– контрольна частина породжуючої матриці (прямокутна з n-k стовпцями та з k рядками у загальному випадку). Породжуюча матриця побудована так, що множення вектора a на цю матрицю продукує кодування з результатом b; вектор b є дозволена до передавання лінією кодова комбінація, котра не має помилок.
;
для a=1101 знайдемо результат кодування b=a×G
b=a×G = 1101×G = 1101 010.
Операція множення вектора на матрицю виконана шляхом множення
компонентів вектора на елементи відповідних рядків матриці, потім стовп- ці просумовано за модулем 2. У складі результату є повторення вектора a (це забезпечила одинична матриця у складі G), а також є контрольна частина (підкреслена) - контрольні розряди кодової комбінації. Кожен контрольний розряд визначено підсумовуванням за модулем 2 тих роз-рядів вектора a, проти яких відповідний стовпець матриці B має одиниці.
9.3 Виявлення помилок
Кодові комбінації, які є елементи n-вимірного лінійного простору (а також групи), можна розбити на дві підмножини: - підмножину (а також підгрупу або k-вимірний підпростір) дозво- лених до передавання кодових комбінацій лінійного коду (результатів ко- дування): - підмножину – решту кодових комбінацій, які заборонені до передавання і можуть з’явитися на приймальному кінці лінії лише внаслі- док виникнення помилок. Одержання на приймальному кінці лінії заборонених кодових комбі- націй свідчить про наявність помилок. Одержання на приймальному кінці дозволених кодових комбінацій ще не свідчить про відсутність помилок. Справа в тому, що перешкоди можуть змінити дозволену кодову комбі- націю так, що то стане інша дозволена кодова комбінація. Віроємність такої події є завжди. Для визначення, чи є конкретна кодова комбінація дозволена є алгоритм, побудований з використаннім того, що скалярний добуток ортогональних векторів дорівнює нулю. Коли є система векторів, які ортогональні всім векторам - дозволеним кодовим комбінаціям і неортогональні у сукупності всім векторам - недозволеним кодовим ком-бінаціям, то обчислення скалярних добутків достатньо для визначення характера кодової комбінації. Для будь-якого лінійного коду (n,k) з породжуючою матрицею G існує двоїстий (рос.- двойственный) лінійний код (n,n-k) з породжуючою матрицею Н. Матриця Н для лінійного кода з породжуючою матрицею G є перевірочною і між матрицями та транспнованими матрицями є такий
Звідси випливає, що b ×Ht=0, оскільки рядки у G є орти для створен- ня вектора b під час кодування. Вираз b ×Ht=0 можна використати для перевірки дозволеності кодової комбінації. Структура матриці H:
(39) Приклад. Використаємо умови прикладу попереднього розділу; маємо
;;
Перевіримо, чи є дозволеною кодова комбінація b=1101010.
Так, кодова комбінація є дозволена, бо вектор с (вектор - показник, вектор синдрому) є нульовий. Перевіримо, чи можна виявити одно- разову помилку. Маємо вектор помилки e =0100000. Якщо визначати-мемо вектор с для вектора b з помилкою за виразом
то для висновків відносно виявлення помилок достатньо множити вектор помилки на транспоновану перевірочну матрицю. Для вектора e =0100000 маємо c =011 і висновок - помилка буде виявлена.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.233.72 (0.084 с.) |
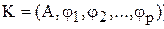
 Якщо у двох алгебраїчних систем
Якщо у двох алгебраїчних систем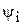
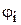 кількість операцій та арність для кожної пари та однакова,
кількість операцій та арність для кожної пари та однакова, , тобто, результат операції над образами елементів першої системи у другій системі має збігатись з образом у другій системі результата операції над елементами в першій си-стемі, то маємо ступінь подібності з назвою гомоморфізм K на M. Цю
, тобто, результат операції над образами елементів першої системи у другій системі має збігатись з образом у другій системі результата операції над елементами в першій си-стемі, то маємо ступінь подібності з назвою гомоморфізм K на M. Цю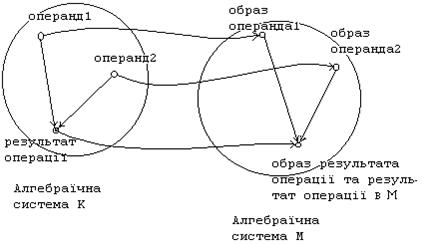
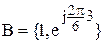 Приклад гомоморфізму групи Z6та підгрупи групи коренів рівняння
Приклад гомоморфізму групи Z6та підгрупи групи коренів рівняння
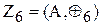 , A={0,1,2,3,4,5) та,
, A={0,1,2,3,4,5) та, 0
0
 1
1 Множина Множина
Множина Множина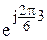 2
2
 A В
A В має назву - кільце з одиницею;
має назву - кільце з одиницею;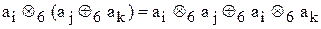
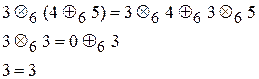 для ai=3, aj=4, ak=5 маємо
для ai=3, aj=4, ak=5 маємо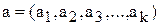 Процедура кодування розглядає двійкове повідомлення, як багато-вімірний вектор (кортеж), і кожному вектору,
Процедура кодування розглядає двійкове повідомлення, як багато-вімірний вектор (кортеж), і кожному вектору,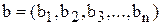 , у якому n-k надлишкових елементів. У бінарному
, у якому n-k надлишкових елементів. У бінарному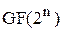 числа з операцією підсумовування розрядами (група). Лінійним кодом
числа з операцією підсумовування розрядами (група). Лінійним кодом

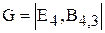 Приклад: лінійний код (7,4), породжуюча матриця,
Приклад: лінійний код (7,4), породжуюча матриця,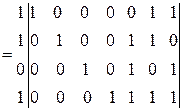
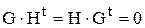 зв’язок:
зв’язок: