Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для характеристики виявляючої здатності кода достатньо мати
транспоновану перевірочну матрицю. Відносно лінійного кода, що роз- глядаємо у прикладі, висновки такі: 1) одноразові помилки будуть виявлені всі, бо у Htнемає жодного нульового рядка; 2) дворазові помилки (дві помилки у кодовій комбінації) будуть виявлені всі, бо у Htнемає однакових рядків; 3) триразові та більшої кратності помилки будуть виявлені не всі, бо є можливість одержання нуля підсумовуванням розрядами трьох або більшої кількості рядків у Ht.
9.4 Виправлення помилок
Якщо кодова комбінація двічи спотворена помилкою з одним і тим же вектором e, помилка зникає і кодова комбінація відновлюється. Це випливає з властивості операції XOR, а саме e Å e =0. Якщо b` = b Å e, то b` Å e = b Å e Å e = b і виправлення відбулося. Але звідки може стати ві- домим вектор помилки e? З попереднього розділу відомо, що вектор синдрому c можна обчис- лити за виразом c = e ×Ht, тобто, вектор с перебуває у відповідності до вектора помилки e і можна побудувати таблицю відповідності, наро-щуючи кратність помилки до появи повторів вектора c. Така таблиця послуговуватиме для визначення вектора помилки e, якщо відомий вектор синдрому c. Таблиця 9-1
В таблиці 9-1 для кожного варіанту трирозрядної кодової комбіна- ції вектора синдрома є відповідний вектор помилки, з чого можна зро- бити висновок відносно виправляючої здатності кода: запропонований у прикладі варіант лінійного кода (7,4) може виправляти всі одноразові по- милки, бо між векторами синдрому та векторами одноразових помилок існує взаємно однозначна відповідність. Апаратна реалізація пристрою для виправлення помилок можлива за поданою нижче структерною схемою:
Постійний запам’ятовуючий пристрій b` Адреса Число з e e
Рис. 9-1
Схема на рис.9-1 для виправлення помилок та збирання статистики помилок використовує постійний запам’ятовуючий пристрій (ПЗП) та пристрій підсумовування розрядами. Кодова комбінація з лінії зв’язку, яка можлива з помилкою, спрямована у ПЗП у якості адреси комірки. В комірці попередньо під час програмування ПЗП записано відповідний
вектор помилки. Вектор помилки з виходу ПЗП потрапляє у систему збору статистики помилок та на один з входів пристрою підсумовування розрядами. На іншому вході пристрою перебуває кодова комбінація з лі- нії. На виході пристрою має з’явитись виправлена кодова комбінація. Для побудови такого пристрою потрібна таблиця для програмування ПЗП. Таку таблицю можна побудувати скориставшись тим, що всі n-розрядні двійкові кодові комбінації створюють групу з операцією підсумовування розрядами, а дозволені до передавання кодові комбінації лінійного коду створюють підгрупу у цій групі. Для того, щоб на дозволені кодові комбі- нації ПЗП реагував видачею нульових векторів помилки, потрібно за ад- ресами, якими є дозволені кодові комбінації, у ПЗП записати нульові вектори помилки. Інший вектор помилки, з тих, які можуть бути виправ- лені (наприклад, вектор помилки 0000001 з рядка з номером 2 у таблиці 9-1), треба записувати за адресами, що є дозволені кодові комбінації, спо- творені саме цим вектором помилки, тобто, адресами з підмножини e1×H - суміжного класу у групі n-розрядних двійкових чисел з підгрупою Н. Виділивши всі суміжні класи матимемо таблицю адрес та вектори по милок з таблиці 9-1, які потрібно записати у ПЗП за цими адресами. Має бути зрозумілим, що вірно виправлені можуть були лише помилки з векторами з таблиці 9-1 для розглянутого лінійного коду.
9.5 Алгебра кодування та декодування циклічним кодом
Лінійні коди через недоліки не набули широкого використання. Підвищення кількості розрядів у повідомленні ускладнює роботу з ма- трицями, вони стають громіздкими, апаратні засоби дорожчають. Під- вищення надмірності менш ефектино впливає на виявляючу здатність ніж у циклічних кодах. Циклічні коди теж можна описати породжуючою матрицею і проводити кодування та декодування за тими ж алгоритмами, що і для лінійного коду, але для них є інші, менш громіздкі, алгоритми. Дозволені до передавання кодові комбінації циклічного коду є елементи ідеала кільця многочленів над GF(2). У розділі 8 наголошува-
лось, що у складі ідеала кільця завжди є елемент, на який можна поді- лити без залишку всі інші елементи ідеала. Тому для прийняття рішен- ня відносно того, чи вважати кодову комбінацію дозволеною, використо-вують ділення полінома, що відображує кодову комбінацію, на утворюю- чий поліном циклічного коду. Ділення та інші дії відбувається за прави-лами проведення операцій у скінченних полях многоч ленів над GF(2).
Назву “циклічний” цей код одержав тому, що операція циклічного зсуву над дозволеною до передавання двійковою кодовою комбінацією дає теж дозволену кодову комбініцію. Операція кодування циклічним кодом полягає у наступному. Нехай маємо P(x) - утворюючий поліном циклічного коду степеня r (елемент ідеалу кільця поліномів, до того ж елемент з найменшим степенем), T(x) - поліном повідомлення користувача;
1) одержуємо T(x)×xr, це зсуває кодову комбінацію ліворуч на r розрядів, вивільнює r місць у кінці повідомлення для контрольних розрядів;
, (40) головний результат - R(x), тобто, залишок від ділення;
має контрольні розряди у вигляді залишку від ділення; 4) перевірка M(x) на дозволеність (декодування) дає
результат ділення на P(x) без залишку, кодова комбінація є дозволена. Якщо циклічний код використовується як виправляючий, то залишок від ділення використовують для пошуку вектора помилки.
9.6 Виявляюча здатність циклічного коду
Якщо під час передавання відбулося спотворення повідомлення, то M(x)®M(x)Åe(x), e(x) – поліном (вектор) помилки. Під час декодування ділення на утворюючий поліном дасть
, (41)
тобто, наявність залишку від ділення залежить лише від полінома помил-
ки. Це означає, якщо ділення не відбудеться без залишку, то помил- ка буде виявлена. За яких умов помилка буде виявлена завжди? 1) Одноразова помилка; поліном помилки має вигляд e(x)=xi; ділення без залишку на утворюючий поліном P(x) можливе лише тоді, коли утворюючий поліном теж складається з одного доданку; якщо
утворюючий поліном складається з більш ніж одного доданку, ділення без залишку неможливе і всі одноразові помилки будуть виявлені;
; (42) ділення без залишку неможливе, якщо степінь утворюючого полінома r³(i-j); за цієї умови дворазові помилки будуть виявлені всі; 3) всі помилки непарної кратності будуть виявлені, якщо утво- рюючий поліном має співмножник (x+1); чому так? Якщо будь-який поліном помножити на x+1, кількість доданків у результата буде пар- на; якщо кількість доданків у поліномі непарна, то у такого полінома немає співмножника x+1; звідси випливає, що у помилок непарної кратності кількість доданків непарна, і у цього полінома немає спів-множника x+1, тому на утворюючий поліном, у якого є такий співмножник, поділити поліном помилки без залишку неможливо; 4) групова помилка буде завжди виявлена, якщо розмір помилки дорівнює або меньше степеня утворюючого полінома (r). Розмір групової помилки це кількість двійкових розрядів між крайніми одиницями век- тора помилки з додаванням числа 2, щоб врахувати крайні одиниці. Якщо розмір групової помилки дорівнює r+1, то невиявлена помилка
можлива лише у одному з 2r-1випадків. Для оцінки віроємності невияв-
(43) Для виявлення помилок у записах на гнучких дисках використо-вують утворюючий поліном за стандартом CRC-16
для виявлення та виправлення помилок у записах на жорстких дисках використовують поліном за стандартом EEC-32
(45) Існує значне різноманіття циклічних кодів з різними корисними властивостями, нами було розглянуто найпростіший код. У пристроях для кодування/декодування циклічних кодів операцію ділення на утворюючий поліном виконують на зсувних регістрах із зворотним зв’язком (з суматорами за модулем 2). Правила побудови структурної схеми пристрою розглянемо на прикладі. Маємо утворюю-
1) Кількість тригерів зсувного регістра має дорівнювати r, r =4; 2) Входи та виходи позначають від x0до xr, як на рис. 9-2
Рис. 9-2 Розмітка входів/виходів тригерів
3) суматори у кількості, на одиницю меншій ніж кількість додан- ків утворюючого полінома, розташовують на входах тригерів, у яких розмітка збігається з виглядом доданків утворюючого полінома (за ви- нятком доданка вищого степеня); 4) виходи тригерів поєднують з входами з однаковою розміткою через суматори або без них; другі входи суматорів поєднують з виходом зсувного регістру: вхід схеми є вхід першого суматора, виходи схеми є
виходи ® вих.1 вих.2 вих.3 вих.4
Рис.9-3. Структурна схема кодера/декодера циклічного коду
Двійкову кодову комбінацію довжиною у n розрядів подають послідовно старшими розрядами вперед на вхід пристрою і через n+r тактів на виходах буде сформовано у двійковому вигляді залишок від ділення полінома кодової комбінації на утворюючий поліном.
10 Основи теорії графів [2,10,15]
10.1 Визначення
1) Орієнтований граф або орграф G=(X,Г) це впорядкована пара множин (X,Г), де Х - непррожня множина вершин графа; Г - багатозначне відображення множини Х на себе. 2) Оскільки багатозначне відображення Г:X®X цілком визначаєть- ся переліком кортежів вигляду (x,y), де x Î X та y Î X, то орграф можна
визначити ще й так: орієнтований граф G =(X, U) є впорядкована пара множин (X, U),
де X є непуста множина вершин орграфа, а U є множина ідентифіка-торів впорядкованих пар елементів з X, що звуться дугами орграфа. Цей варіант визначення охоплює мультиграфи - орграфи, де трапляються декілька дуг між парою вершин. 3) Нехай u – дуга орграфа, u =(x, y). Вершина x є початок дуги u, а вершина y є кінець дуги u. При цьому кажуть, що дуга u виходить з вершини x і входить або заходить у вершину у. В обох випадках ка- жуть, що дуга інцидентна вершині. Дуга (x,x) є петля вершини x. Вершини, поєднані дугою мають назву - суміжні. 4) Орієнтований мультиграф - таку назву має граф, у якому є хо- ча б одна двійка вершин, поєднана декількома дугами одного напрямку. Симетричний, неорієнтований або просто граф відрізняється тим, що з існування дуги (x,y) випливає існування дуги (y,x). Замість двох дуг протилежних напрямків вважають наявним одне ребро графа. 5) Повний орграф має дугу з кожної вершини в будь-яку іншу, повний орграф є завжди симетричний, тобто, повний граф.
вершини x і має позначку. Кількість дуг, що заходить у вершину x,є напівступінь заходу
(46)
8) Множина вершин, які є початками дуг з позначають че-
Г або Г(x) (це вершини нащадки). 10) Вершина, інцидентна тільки дугам вигляду (x,x), має назву “ гола ”. Вершина, яка неінцидентна жодній дузі, має назву “ ізольова- на ”. Її ступінь дорівнює нулю.
логічно вихід орграфа є вершина, у якої. 12) Шлях m[a,b] з вершини а у вершину b це послідовність вер- шин та дуг, яка (можливі інші визначення) виглядає так:
13) Шлях є елементарний, якщо жодна вершина у ньому не по- вторюється. Шлях є простий, якщо жодна дуга у ньому не повторюється. 14) Якщо існує шлях m[a,b], то кажуть, що - вершина b є досяжна з вершини a, або - вершина a досягає вершини b. 15) Орграф є сильнозв’язний, якщо для будь-якої пари вершин кожна з них досяжна з іншої. 16) Шлях звуть “ ейлерів ”, якщо у ньому присутні всі дуги орграфа одноразово кожна. 17) Шлях звуть “ гамільтонів ”, якщо у ньому присутні всі вершини орграфа одноразово кожна. 18) Шлях m[a,a] звуть контуром. Початок і кінець контура збі- гаються. 19) Контур є ейлерів, якщо всі дуги орграфа присутні одноразово. 20) Довжина шляху або контуру є кількість дуг у ньому. 21) Якщо G=(X,U) є орграф, то Н=(Y,V) є - частковий граф, якщо YÍX, VÍU, підмножина дуг з вершинами; - суграф або остовий підграф (X – остов, скелет), якщо Y=X, VÍU, тобто, є ізольовані вершини); - підграф, якщо YÍX, VÍU, підмножина вершин з цілком інцидент-ними тим вершинам дугами.
22) Сильнозв’язний підграф орграфа має назву “ зона ”. Зона, макси-мальна відносно включення вершин, має назву “ компонент сильної зв’язності ” або “ бікомпонент ”. На рис. 10-1 підграф з вершинами
Рис. 10-1 Орграф G
V1,V2,V4 є зона, а з вершинами V1,V2,V3,V4 є бікомпонент. 23) Підграф, який має одну початкову (вхідну) і одну кінцеву вершину має назву “ гамак ”. На рис. 10-1 підграфи з вершинами S,V6,V7,V8,V9,V5 та S1,V1,V3,V4,V2,V5,T є гамаки. 24) Гамак, який відповідає умовам: - початкова та вихідна вершина гамака лежать на кожному шляху з початкової до кінцевої вершини s-t орграфа (тобто орграфа з одним входом та з одним виходом), - початкова вершина недосяжна з виходу гамака, - не існує іншого гамака, що відповідає двом попереднім умовам і є у складі цього гамака має назву “ лінійний компонент орграфа ”. На рис. 10-1 підграф орграфа G з вершинами V5,V10,T - є лінійний компонент орграфа G. 25) Неорієнтований (симетричний) граф (або просто граф) G=(X,U), де X є множина вершин графа, а U є множина невпорядкова- них пар (або ідентифікаторів пар на випадок мультиграфа). Пари елементів є ребра графа. Поняття суміжності, ступіня вершин (напівступіня немає) аналогічні тим, що визначені для орграфа. Входом та виходом можуть бути будь-які вершини. Замість дуг у графа – ребра, замість шляху - лан - цюг, замість контура – цикл. Для ланцюгів та циклів визначені поняття простоти, ейлеровості, гамільтоновості, а також довжини. Граф є зв’яз- ний, якщо кожна пара вершин зв’язана ланцюгом. Зберігаються поняття часткового графа, суграфа та підграфа (з заміною у визначеннях множини дуг на множину ребер. 26) Дерево це - зв’язний неорієнтований граф без циклів або - граф, де будь-які дві вершини з’єднані простим ланцюгом, або - граф зв’язний і має ½X½+1 ребро, або - граф не має циклів і має ½X½+1 ребро, або - граф не має циклів, але додання ребра між будь-якими двома вер- шинами призводить до появи одного цикла, або - граф зв’язний, але втрачає цю властивість після видалення будь- якого ребра. Тобто маємо низку визначень-властивостей дерева. 27) Вершина ступіня 1 має назву “висяча”. Будь-яке дерево має не менше ніж дві висячі вершини. 28) Відстань від вершини x до найвіддаленої вершини називають ексцентриситет ом вершини x і позначають як e(x), e(x)=maxm[x,y]. 29) Найменьший ексцентриситет вершин є радіус дерева T, це позначають як r(T). 30) Центральна вершина дерева це вершина, у якій ексцентриситет дорівнює радіусу. Центр дерева це множина центральних вершин. 31) Незв’язний граф, який має у складі підграфи-дерева у якості областей зв’язності є ліс. 32) Дерево може покривати інший граф, якщо всі вершини дерева належать графу і дереву. Тільки зв’язні графи мають покриваючі дерева і тільки дерево має єдине покриття деревом. Приклад. Є граф – дерево T (рис. 10-2). Задача – визначити радіуc та центр дерева T. Розв’язок. Після визначення ексцентриситетів вершин
Рис.10-2. До визначення радіуса та центра дерева.
дерева знайдено мінімальний ексцентриситет, тобто, радіус дерева r(T)=4; центр дерева T це дві вершини, позначені чорним кольором. 33) Ордерево, орієнтований граф типу “дерево”. Ордерево, що росте з кореня, тобто, має єдину вершину – вхід, - має єдиний для кожної вершини шлях з кореня до вершини. 34) Впорядковане дерево - задано порядок переліку піддерев. 35) Однорідний граф той, у якого ступіні всіх вершин однакові. 36) Бінірне ордерево – з вершини виходить не більше двох дуг, m-арне дерево - виходить не більше m дуг. 37) Плоский граф – граф, вершини якого можуть бути розташовані на площині так, що ребра графа не перетинаються зовні вершин. Така властивість графа електропровідних смуг є умовою використання друко-ваного монтажу електронних пристроїв. 38) Несепарабельний або двозв’язний граф це такий, у якого вида- лення вершини (разом з інцидентними дугами) не порушує зв’язності. 39) Двочастковий граф це граф, у якого вершини розбиті на дві підмножини і вершини, інцидентні будь-якому ребру, завжди належать різним підмножинам; n-частковий граф - множина вершин розбита на n підмножин, умови інцидентності вершин такі ж.
10.2 Способи задання графів
10.2.1 Геометричне подання - рисунок. Використовують з метою ілюстрації та як робочий документ (карти, схеми). Незручний з підвищен-ням кількості вершин. 10.2.2 Матриця інцидентності. Це прямокутна матриця, розмітка вздовж рядка - ідентифікатори вершин графа, розмітка вздовж
- якщо вершина j є кінець дуги і, то = 1;
- якща дуга чи ребро є петля, то =a, a¹0, a¹-1, a¹1. В матриці інцидентності не більше двох елементів рядка є відмінні від нуля. Такий спосіб задання графів є універсальний, але не є економіч- ний щодо пам’яті ЕОМ. 10.2.3 Список ребер (дуг). Тут у кожному рядку є відповідні номери дуги та вершин, що їй інцидентні. Це також універсальний але набагото більш економічний спосіб щодо пам’яті ЕОМ. 10.2.4 Матриця суміжності графа (орграфа). Це квадратна матриця
елементи дорівнюють нулю. Неорієнтований граф має матрицю, яка си- метрична відносно головної діагоналі. Спосіб має обмеження – неможливо задавати мультиграфи. 10.2.5 Матриця досяжності орграфа. Це також квадратна матриця, де номери рядків та стовпців це номери вершин орграфа. Елементи матри-ці набувають значення одиниці лише тоді, коли існує шлях з вершини, що має номер рядка, у вершину, що має номер стовпця матриці. Цей спосіб задання не дозволяє розрізнити зв’язні графи. Для кожного орграфа можна задати матрицю досяжності. Але не всяка довільна матриця є матрицею досяжності орграфа, бо віднайти з її допомогою інші варіанти задання іноді неможливо (орграф не існує). Приклад. Для орграфа G4 (рис.10-3) приготувати задання різними способами.
Рис.10-3 Орграф G4 1) Матриця інцидентності орграфа G4
V1 V2 V3 V4 V5 V6 V7
l2 -1 0 0 0 0 0 1 -1 0 0 0 0 0 1 l3 1 0 -1 0 0 0 0 1 0 -1 0 0 0 0 l4 0 0 -1 1 0 0 0 0 0 -1 1 0 0 0 l5 0 -1 1 0 0 0 0 або I(G4) = 0 -1 1 0 0 0 0 l6 0 2 0 0 0 0 0 0 2 0 0 0 0 0 l7 0 1 0 0 0 0 -1 0 1 0 0 0 0 -1 l8 0 -1 0 0 1 0 0 0 -1 0 0 1 0 0 l9 0 0 -1 0 1 0 0 0 0 -1 0 1 0 0
Матрицю ліворуч можна розглядати як попередній етап побудови матриці інцидентності орграфа G4. 2) Список дуг виглядає так:
l1 V1 V2 l2 V1 V7 l3 V3 V1 l4 V3 V4 l5 V2 V3 l6 V2 V2 l7 V7 V2 l8 V2 V5 l9 V3 V5
Зауважимо, що задання мультиграфа таким способом проблем не задасть, а ось ізольована вершина тут ніяк не позначена. 3) Матриця суміжності орграфа G4.
V1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 V2 0 1 1 0 1 0 0 0 1 1 0 1 0 0 V3 1 0 0 1 1 0 0 1 0 0 1 1 0 0 V4 0 0 0 0 0 0 0 або С(G4) = 0 0 0 0 0 0 0 V5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 V6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 V7 0 1 0 0 0 0 0 0 1 0 0 0 0 0
Кількість одиниць у матриці дорівнює кількості дуг орграфа, задати мультиграф неможливо, бо це також матриця бінарного відношення су- міжності орграфа G і тому припустимі лише 0 та 1 у якості елементів. 4) Матриця досяжності орграфа G4. Така матриця інформативна саме для орграфа, бо для зв’язного графа всі елементи матриці є одиниці, а для графа з декількома обла- стями зв’язності у матриці буде декілька квадратних підматриць суцільно з одиницями, у цих підматриць головна діагональ розташована на годовній діагоналі матриці досяжності. Для орграфа все інакше:
V1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 V2 1 1 1 1 1 0 1 1 1 1 1 1 0 1 V3 1 1 1 1 1 0 1 1 1 1 1 1 0 1 V4 0 0 0 0 0 0 0 або Д(G4) = 0 0 0 0 0 0 0 V5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 V6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 V7 1 1 1 1 1 0 1 1 1 1 1 1 0 1
10.3 Відношення і графи
Граф (орграф) дає наглядне геометричне зображення відношень на множинах, їх властивостей. Рефлексивність виглядає як наявність петель на всіх вершинах орграфа (графа). Антирефлексивність – відсутність пе- тель. Симетричність виглядає як наявність ребер графа, або наявність двох зустрічних дуг, що поєднують суміжні вершини. Антисиметричність – цілковита відсутність зустрічних дуг між суміжними вершинами. Транзитивність виглядає як обов’язкова наявність для кожних двох послідовних дуг (ребер) однієї дуги (ребра), що поєднує ті ж кінцеві вершини. Якщо на орграфі є вершини, які можна розглядати як пари за принципом досяжності (тобто друга досяжна з першої), то сукупність таких пар складе відношення еквівалентності, якщо на графі вони ство- рюють контур. Якщо створюють єдиний шлях без самоперетинів то мно- жина пар складе відношення строгого порядку, а при наявності петель на всіх вершинах – відношення нестрогого порядку.
10.4 Характеристики графів
Йдеться про числові характеристики графів. Цикломатичне число графа G, який має n вершин, m ребер, r областей зв’язності можна вирахувати за формулою n(G) = m – n + r. (48) Це число є кількість незалежних циклів на графі. Залежний цикл це той, що побудований тільки з ребер, які належать іншим циклам. У іншому випадку цикл є незалежний. Під час аналізу електричних кіл - кількість рівнянь, складених за методом контурних струмів, дорівнює цикломатичному числу графа електричного кола. Хроматичне число графа G. Йдеться про таке “ розфарбовуван-ня” вершин графа, коли суміжні вершини мали б різні кольори. Най- менша кількість кольорів p має назву - хроматичне число графа, а граф є p -хроматичним, а також має позначку g(G), тобто g(G) = p. Якщо g(G) =2, то граф є біхроматичний. Достатня умова біхроматичності графа - наявність циклів лише парної довжини. Визначення цикломатично-го числа не завжди легка задача (ЕОМ!). Теорема про 5 фарб стверджує, що p=5 достатньо для будь-яких плоских графів.
10.5 Деякі теореми про графи
1) Для кожного скінченного графа існує його геометричне зобра- ження у тривимірному евклідовому просторі. 2) Теорема Понтрягіна-Куратовського про плоскі графи. Для того, щоб граф вважати плоским, необхідно і достатньо, щоб він не мав у складі ніякого графа, який можливо було б стиснути до повного графа з п’ятьма вершинами або до графа “обслуговування” з шістьма вершинами (дво- часткового графа 3+3 вершини та 9 ребер, стиснути – означає замінити плоскі гамаки ребрами та вочевидь плоскі підграфи вершинами). 3) У однорідного графа, де r =deg(x)=const кількість ребер
(49) де n – кількість вершин, r – ступінь вершин. 4) У графа кількість вершин непарного ступіня завжди парна. 5) Зв’язний граф з парними ступінями вершин має ейлерів шлях. (Ейлерів граф – план добре продуманої виставки, де відвідувачі не ходять двічи біля експозіцій.) 6) Для того, щоб ланцюг m[a,b] був ейлеровим, необхідно, щоб вершини a та b були єдиними вершинами непарного ступіня. 7) У повному орграфі завжди є шлях через всі вершини (Гамільтонів шлях). 8) Теорема Келі (1857). Кількість остових дерев (підграфів повного
шин остова[12]. Приклад: рис. 10-4, для n=4 маємо N = 42= 16 дерев
остов варіанти остових дерев
Рис. 10-4 До підрахунку кількості остових дерев. 10.6 Гамільтонів шлях на багатовимірному одиничному кубі та рефлексні коди. Уявімо куб з ребрами довжини 1. Якщо ребра куба для нас є ребра графа, а вершини куба є вершини графа, то на графі можна побудувати гамільтонів шлях, як це показано виділенням відповідних ребер на ри- сунку 10-6. Якщо у якості ідентифікаторів вершин використати кортежі, де елементи є координати вершин, то трійки координат можна вважати двій- ковими кодовими комбінаціями, оскільки кожна з координат може мати лише значення 0 або 1. Послідовність координат вершин на гамільтоново-му шляху є послідовність кодових комбінацій рефлексного кода (у даному випадку трирозрядного кода – показана на рис.10-6).
Рис.10-5 Гамільтонів шлях на тривимірному одиничному кубі
Очевидні такі властивості послідовності кодових комбінацій: 1) сусідні кодові комбінації відрізняються лише у одному розряді; 2) за винятком одного стовпця (х) комбінації симетрично розташо-вані відносно лінії розділу на рис.10-5, тобто, має місце дзеркальне відбит- тя, англійською мовою- reflection, звідси назва – рефлексивний; 3) сума елементів кодової комбінації за модулем 2 у послідовності дає чергування 0101010101. Гамільтонів шлях на такому кубі не є один єдиний. Якщо куб п’ятивимірний, кількість шляхів сягає N=237230 (визначено за допомогою ЕОМ БЕСМ-4 у 1972 році), тобто, така є кількість п’ятирозрядних рефлек- сивних кодів [12]. Один з них має назву “код Грея”. Це той, для якого алгоритм перетворення двійкової кодової комбінації у кодову комбінацію кода Грея, полягає у наступному: двійкову кодову комбінацію та цю ж комбінацію, але зі зсувом на один розряд праворуч з втратою розряда, що вийшов за межу, підсумовують розрядами (операція XOR). Одержана комбінація є комбінація кода Грея. Наприклад, маємо кодову комбінацію двійкового коду - 1101000101 після зсуву маємо 110100010 підсумовування розрядами дає 1011100111 - кодову комбінацію кода Грея. Зворотне перетворення можливе за таким алгоритмом: старший розряд кодової комбінації Грея не змінюється і його значення потрапляє у старший розряд результата; до його значення додають за модулем 2 значення наступного розряду кодової комбінації Грея; результат додаван-ня є значення наступного розряду перетвореної кодової комбінації; до нього таким же чином додають наступний розряд кодової комбінації Грея і так надалі, поки буде визначено молодший розряд результата. Коди Грея використовуються у перетворювачах вугла обертання ва-ла у код з безпосереднім відліком результата; їх застосування сприяє однозначності відліку результата під час переходу від однієї кодової ком-бінації до іншої. Лічильники у коді Грея вікористовують, коли є потреба контролювати наявність порушень у роботі синхронізаторів у стрічкових магнітних запам’ятовуючих пристроях.
10.7 Графи як моделі програм, даних та процесів [15]
1) Керуючий граф. Багато задач аналізу програм, що виникають у спробах оптимізації, трансляції, тестування та т. н., можуть бути значно спрощені, якщо їх розглядати на теоретико-графових моделях. Орграф G=(X,U) звуть керуючим графом (р-графом, графом пере- ходів), якщо виконано умови:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.13.201 (0.432 с.) |






 комірки комірки
комірки комірки


 Å b
Å b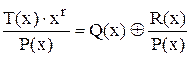 2) результат попередньої дії ділимо на P(x)
2) результат попередньої дії ділимо на P(x)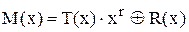 3) кодоване повідомлення
3) кодоване повідомлення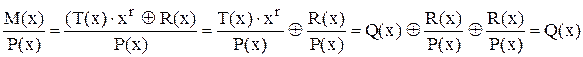
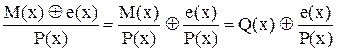
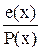
 2) дворазові помилки; поліном помилки має вигляд
2) дворазові помилки; поліном помилки має вигляд леної помилки іноді використовують вираз
леної помилки іноді використовують вираз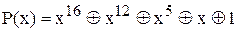 (44)
(44)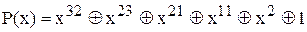
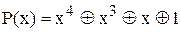 чий поліном степеня r=4.
чий поліном степеня r=4.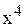

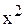






















 виходи тригерів регістру, як це виглядає на рис. 9-3.
виходи тригерів регістру, як це виглядає на рис. 9-3.


 вхід Т1 Т2 Т3 Т4
вхід Т1 Т2 Т3 Т4

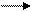
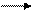
 Å Å Å
Å Å Å 6) Кількість дуг, що виходить з вершини x,є напівступінь виходу
6) Кількість дуг, що виходить з вершини x,є напівступінь виходу вершини x і має позначку.
вершини x і має позначку.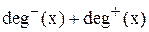
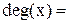
 Загальна кількість дуг, що інцидентні вершині x,є ступінь верши-ни х і має позначку.
Загальна кількість дуг, що інцидентні вершині x,є ступінь верши-ни х і має позначку.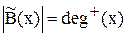
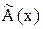
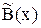 7) Множина дуг, що заходить у вершину x, має позначку.
7) Множина дуг, що заходить у вершину x, має позначку.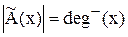 . Аналогічно - множина дуг, що виходить з вер-
. Аналогічно - множина дуг, що виходить з вер-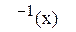
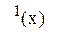 9) Множина вершин, які є кінцями дуг з, позначають через
9) Множина вершин, які є кінцями дуг з, позначають через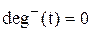
 11) Вхід або початок орграфа є вершина, у якої. Ана-
11) Вхід або початок орграфа є вершина, у якої. Ана- (47)
(47)

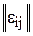 стовпця - ідентифікатори дуг або ребер. Елементи матриці,
стовпця - ідентифікатори дуг або ребер. Елементи матриці,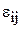 тобто,, де i - номер рядка (а також дуги або ребра);
тобто,, де i - номер рядка (а також дуги або ребра);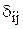
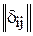 , елементи якої, дорівнюють одиниці лише, якщо вершина i є інцидентна початку дуги, а вершина j інцидентна кінцю дуги, інакше
, елементи якої, дорівнюють одиниці лише, якщо вершина i є інцидентна початку дуги, а вершина j інцидентна кінцю дуги, інакше

 l1 -1 1 0 0 0 0 0 -1 1 0 0 0 0 0
l1 -1 1 0 0 0 0 0 -1 1 0 0 0 0 0
 V1 V2 V3 V4 V5 V6 V7
V1 V2 V3 V4 V5 V6 V7
 V1 V2 V3 V4 V5 V6 V7
V1 V2 V3 V4 V5 V6 V7
 графа) з розміченими вершинами дорівнює, n – кількість вер-
графа) з розміченими вершинами дорівнює, n – кількість вер-