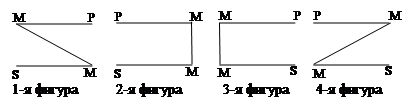Дедуктивные и индуктивные умозаключения. Законы логики

Умозаключения. В широком смысле умозаключение – логическая операция, в результате которой из одного или нескольких принятых утвержде­ний (посылок) получается новое утверждение – заключение (вы­вод, следствие). В зависимости от того, существует ли между посылками и зак­лючением связь логического следования, можно выделить два вида умозаключений.

В основе дедуктивного умозаключения лежит логический закон, в силу чего заключение с логической необходимостью вытекает из принятых посылок. От истинных посылок оно всегда ведет к истинному заключению.

В индуктивном умозаключении связь посылок и заключения опи­рается не на закон логики, а на некоторые фактические или пси­хологические основания, не имеющие чисто формального характера. В таком умозаключении заключение не следует логически из посылок и может содержать информацию, отсутствующую в них. Индукция дает только вероятные, или правдоподобные, заключения, нуждающиеся в даль­нейшей проверке.

Во всех случаях, когда требуется рассмотреть какие-то явления на основании уже известного общего правила и вывести в отноше­нии этих явлений необходимое заключение, мы умозаключаем по форме дедукции.

Рассуждения, ведущие от знания о части предметов (частного знания) к знанию обо всех предметах определенного класса (общему знанию), – это типичные индукции. Всегда остается вероятность того, что обобщение окажется поспешным и необос­нованным («Наполеон – полководец; Суворов – полководец; зна­чит, каждый человек полководец»). Нельзя, однако, отождествлять дедукцию с переходом от общего к частному, а индукцию – с переходом от частного к общему. Дедукция – это выведение заключений, столь же достоверных, как и принятые посылки. К индуктивным умозаключениям отно­сятся как переходы от частного к общему, так и аналогия, установление причинных связей, подтверждение следствий, целе­вое обоснование и т. д.

Подчеркивая важность дедукции в процессе развертывания и обоснования знания, не следует, однако, отрывать ее от индукции и недооценивать последнюю. Почти все общие положения, включая и научные законы, являются результатами индуктивного обобще­ния. В этом смысле индукция – основа нашего знания. Сама по себе она не гарантирует его истинности и обоснованности, но она порождает предположения, связывает их с опытом и тем самым сообщает им определенное правдоподобие, более или менее высо­кую степень вероятности. Опыт – источник и фундамент человече­ского знания. Индукция, отправляющаяся от того, что постигается в опыте, является необходимым средством его обобщения и сис­тематизации.

Существенным является следующее традиционное ограничение: имена, встречающиеся в силлогизме, не должны быть пустыми или отрицательными. Нельзя с помощью силлогизма рассуждать, ска­жем, о русалках или треугольных квадратах.

Слова и сло­восочетания, выражающие понятия, фи­гурирующие в силлогизме, называют его терминами. В каждом силлогизме имеется три термина: меньший, больший и средний. Термин, соответствующий субъекту (S) заключения, носит название меньшего термина. Термин, соответствующий предикату (Р) заключения – больший термин. Термин, который присутствует в посылках, но отсутствует в заключении, носит название среднего термина (М). Логическая форма силлогизма: Все М суть Р. Все S суть М. Следовательно, Все S суть Р.

В силлогизме на основании установления отношений меньшего и большего терминов к средне­му термину в посылках устанавливается отношение между меньшим и большим терминами в заключении. Та посылка, в которую входит больший термин, носит название большей посылки, в которую входит меньший термин – меньшей посылки. Средние термины в силлогизме могут распо­лагаться следующим образом:

1) сред­ний термин М может быть субъектом в большей посылке и предикатом в меньшей (1-я фигура);

2) средний тер­мин может быть предикатом в обеих по­сылках (2-я фигура);

3) средний термин может быть субъектом в обеих посылках (3-я фигура);

4) средний термин может быть предикатом в большей посылке и субъектом в меньшей (4-я фигура).

 

Схе­матически фигуры изображаются так:

 

Силлогизм 1-й фигуры	Все металлы (М) электропроводны (Р) Стронций ( S ) металл (М) Стронций электропроводен.
Силлогизм 2-й фигуры	Все рыбы (Р) дышат жабрами (М) Кашалоты (S) не дышат жабрами (М) Кашалоты – не рыбы.
Силлогизм 3-й фигуры	Все бамбуки (М) цветут один раз в жизни (Р) Все бамбуки (М) расте­ния ( S ) Некоторые растения цветут один раз в жизни.
Силлогизм 4-й фигуры	Все киты (Р) – млекопитающие (М) Ни одно млекопитающее (М) не есть рыба ( S ) Ни одна рыба не есть кит.

 

Чтобы получить истинное заключение следует соблюдать правил для терминов и для посылок.

Правила терминов: 1) в силлогизме должно быть только три термина; 2) средний термин должен быть распределен, по крайней мере в одной из посылок; 3) термин распределен в заключении, если и только если он распределен в посылках.

Правила посылок: 1) из двух отрицательных посылок нельзя сделать никакого заключения; 2) если одна из посылок отрицательная, то заключение должно быть отри­цательным; 3) из двух частных посылок нельзя сделать заключения; 4) если одна из посылок частная, то и заключение должно быть частным

Правила 1-й фигуры: большая посылка должна быть общей, а меньшая – утвердительной. Правила 2-й фигуры: большая посылка должна быть общей и одна из посылок, а также заключение – отрицательными. Правила 3-й фигуры: меньшая посылка должна быть утвердительной, а заключение – частным. Правила 4-й фигуры: если большая посылка утвердительная, то меньшая должна быть общей; если есть отрицательная посылка, то большая должна быть общей.

Модусами фигур силлогизма называются раз­новидности его фигур отличающиеся ка­чественной и количественной характе­ристикой входящих в них посылок и заключения. Посылка и заключение, т.о., в каждом случае могут выступать как суждения вида А, Е, I, О (см.: Суж­дение). На первом месте в символическом выражении модуса записывается боль­шая посылка, на втором – меньшая, на третьем – заключение. Так, выражение для модуса ЕIО означает, что большая посылка в нем является общеотрица­тельным суждением, меньшая – частно-утвердительным, а заключение – частно-отрицательным. Всего с точки зрения всевозможных сочетаний посылок и за­ключения в каждой фигуре насчиты­вается 64 модуса. В четырех фигурах насчитывается 64 х 4 = 256 модусов. Из них правильными (т. е. такими, кото­рые при истинности посылок всегда дают истинное заключение) может быть 24, включая и т. наз. ослабленные модусы, т. е. такие, для которых существуют мо­дусы, дающие более сильные заключе­ния. Модус считается более слабым, если мы получаем в заключении сужде­ния вида I, и О, хотя можем получить соответственно суждения А и Е. Не­ослабленных модусов фигур С. – 19. Правильные модусы 1-й фигуры: ААА, ЕАЕ, А I I, ЕIО; 2-й фигуры: ЕАЕ, АЕЕ, Е I О, АОО; 3-й фигуры: ААI, IАI, АII, ЕАО, ОАО, Е IО; 4-й фигуры: ААI, AЕЕ, IАI, ЕАО, ЕIО.

Закон логики – выражение, содержащее только логические константы и переменные и являющееся истинным в любой предметной области. Логических законов бесконечно много. Однородные законы объединяются в логические системы, которые называются логиками.

1. Закон противоречия (непротиворечия) – высказывание и его отрицание не могут быть вместе истинными (неверно, что А и не-А). Закон требует непротиворечивости, отсюда его название – закон непротиворечия. Логическое противоречие состоит в том, что высказывание и его отрицание говорят об одном и том же предмете, рассматриваемом в одном и том же отношении. То что утверждается в одном, отрицается в другом. Следовательно, никакое высказывание не является вместе истинным и ложным. Другая формулировка: из двух противоречащих друг другу высказываний одно является ложным.

2. Закон исключенного третьего – из двух противоречащих высказываний одно является истинным (А или не-А). Истинность отрицания равнозначна ложности утверждения. В силу этого каждое высказывание является истинным или ложным, другого не дано. Отсюда название закона – исключение третьего.

3. Закон тождества – если утверждение истинно, то оно истинно (если А, то А).

4. Законы контрапозиции позволяют с помощью отрицания менять местами основание и следствие условного высказывания.

1-й закон контрапозиции: если первое влечет второе, то отрицание второго влечет отрицание первого («Если верно, что число, делящееся на шесть, делится на три, то верно, что число не делящееся на три, не делится на шесть»).

2-й закон: если верно, что если не первое, то не второе, то верно, что если второе, то первое («Если верно, что рукопись, не получившая положительного отзыва, не публикуется, то верно, что публикуемая рукопись имеет положительный отзыв». «Если нет дыма, когда нет огня, то если есть огонь, то есть и дым»).

3-й закон: если дело обстоит так, что если А, то не-В, то если В, то не-А («Если квадрат не является треугольником, то треугольник не квадрат»).

4-й закон: если верно, что если не-А, то В, то если не-В, то А («Если не являющееся очевидным сомнительно, то не являющееся сомнительным очевидно»).

5. Модус поненс и модус толленс. «Модусом» в логике называется разновидность некоторой об­шей формы рассуждения. Далее будут перечислены четыре близких друг другу модуса.

Модус поненс, называемый иногда гипотетическим силлогизмом, позволяет от утверждения условного высказывания и утверждения его основания перейти к утверждению следствия этого высказывания: Если А, то В. А. Следовательно, В

Благодаря этому модусу от посылки «если А, то В», используя посылку «А», мы как бы отделяем заключение «В». На этом основании данный модус называется «правилом отделения», в соответствие с которым рассуждение идет от утверждения основания истинного условного высказывания к утверждению его следствия. Это логически корректное движение мысли иногда путается со сходным, но логически неправильным ее движением от утвержде­ния следствия истинного условного высказывания к утверждению его основания. Так, рассуждение – Если А, то В. В. Следовательно, А – логически некорректно. Рассуждая по последней схеме, можно прийти от истинных посылок к ложному заключению. Против сме­шения правила отделения с этой неправильной схемой рассуждения предостерегает совет: от подтверждения основания к подтвержде­нию следствия рассуждать допустимо, от подтверждения следствия к подтверждению основания – нет.

Модусом толленсом называется следующая схема рассуждения: Если А, то В. Не-В. Следовательно, не-А.

Посредством этой схемы от утверждения условного высказы­вания и отрицания его следствия осуществляется переход к отрицанию основания. По схеме модус толленс идет процесс фальсификации, установления ложности теории или гипотезы в результате ее эмпирической проверки. Из проверяемой теории Т выводится некоторое эмпирическое утверж­дение А, т. е. устанавливается условное высказывание «если Т, то А». По­средством эмпирических методов познания (наблюдения, измерения или эксперимента) предложение А сопоставляется с реальным положе­нием дел. Выясняется, что А ложно и истинно предложение не-А. Из посылок «если Т, то А» и «не-А» следует «не- Т», т. е. ложность теории Т.

С модусом толленсом нередко смешивается внешне сходное с ним умозаключение: Если А, то В; неверно А. Следовательно,неверно В.

В последнем умозаключении от утверждения условного выска­зывания и отрицания его основания осуществляется переход к отрицанию, его следствия, что является логически некорректным шагом. Рассуждение по такой схеме может привести от истинных посылок к ложному заключению. Например:

Если бы глина была металлом, она была бы пластична.

Но глина не металл.

Неверно, что глина пластична.

Против смешения модуса толленса с данной некорректной схе­мой рассуждения предостерегает совет: от отрицания следствия условного высказывания заключать к отрицанию основания этого высказывания можно, а от отрицания основания к отрицанию следствия – нет.