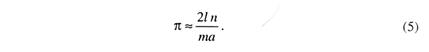Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зв'язок теорії ймовірностей з теорією множин
Множину всіх можливих наслідків випробування називають основним простором або простором елементарних подій (наслідків) і позначають Q. Наслідок позначають со. Випадковою подією (наслідком) називається будь-яка підмножинаЛ простору Q, тобто будь-яка множина наслідків. Наслідки, які утворюють подію А, називають сприятливими для А (соє А). Подія А настає тоді і тільки тоді, коли настає елементарна подія (наслідок), сприятлива для А. Тому теорія ймовірностей і теорія множин мають багато спільного. Втім, в них йдеться про одне й те саме різними словами, що видно з такої таблиці:
Приклад. Підкидають два гральних кубики. Подія А - сума очок, які з'явились, дорівнює 10; подія В - принаймні один раз з'явиться шістка. Опишіть простір елементарних подій та події A U В і А ∩ В. Простір елементарних подій, або множину можливих наслідків випробування, можна записати як набір усіх можливих впорядкованих пар чисел від 1 до 6 (кожну із шести граней першого кубика можна розглядати у парі з будь-якою гранню другого кубика). Отже, Ω = {(1; 1), (1; 2),...(1; 6), (2; 1),..., (6; 5), (6; 6)}. Всього за правилом добутку маємо 6 • 6 = 36 елементів. Подію А задаємо переліком елементів, які її складають:
А = {(4; 6), (5; 5), (6; 4)}.
Аналогічно
В={(6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6), (1; 6), (2; 6), (3; 6), (4; 6), (5; 6)}.
Об'єднання A U В - подія, яка полягає в тому, що відбудеться хоча б одна з подій А або В. Тому A U В означає, що або сума очок на гранях, які випали, дорівнює 10, або принаймні один раз з'явиться шістка. Оскільки елементи (4; 6) і (6; 4) входять одночасно ідо А, ідо В, то
A U B = ((5; 5)}U B. Подія А ∩ В складається з двох елементів, які входять і до А, і до В:
A ∩ B = {(4; 6), (6; 4)}. Геометричні ймовірності
Класичне означення ймовірності ґрунтується на тому, що випробування має скінченну кількість наслідків. Проте є досліди, які мають нескінченну кількість наслідків. Наприклад, нехай на площині міститься область Ω. і в ній міститься інша область А (рис. 300).
Припустимо, що в область Ω навмання кидають точку. Як визначити ймовірність того, що кинута точка потрапить до області А? Природно вважати, що ймовірність попадання точки до області А пропорційна площі цієї області і не залежить від розміщення та форми цієї області.
Підмножини області Ω, які мають площу, називатимемо в такому разі випадковими подіями. Якщо А - випадкова подія, то вважатимемо, що
де S(A) – площа A, S(Ω.) -площа Ω. Ймовірності, що подаються як відношення площ областей (довжин відрізків, об'ємів тіл), називають ще геометричними ймовірностями. Приклад 1. Знайти ймовірність того, що навмання взята точка з круга радіуса R належатиме квадрату, вписаному в коло, яке обмежує круг (рис. 301).
За означенням геометричної ймовірності маємо
де S1 - площа квадрата A ВCD; S - площа круга радіуса R. Оскільки АВ2 = 2R2, то S1 = 2R2. Тому
На перший погляд здається, що геометричні ймовірності є мало корисними для застосувань. Проте це не так. Багато задач, серед яких і ті, що висуваються практикою, врешті-решт зводяться до відшукання ймовірності попадання точки в деяку область. Приклад 2 (задача Бюффона). Нехай на площині проведено паралельні прямі так, що відстань між сусідніми прямими дорівнює 2а. На площину навмання кидають голку завдовжки 2l, l<а. Яка ймовірність того, що голка перетне якусь із цих прямих? Положення голки однозначно визначається величиною кута де та відстанню від середини голки до найближчої прямої (рис. 302). Отже, можна взяти за простір Ω елементарних наслідків прямокутник
Точки, координати яких задовольняють нерівності (2), утворюють фігуру, заштриховану на рис. 303. Згідно з рівністю (1) площа цієї фігури, поділена на площу прямокутника, і буде дорівнювати шуканій імовірності. Площа прямокутника
Формула (3) є корисною при розв'язуванні багатьох задач. Зокрема, користуючись цією формулою, можна наближено обчислити число п. Справді, з формули (3) маємо
Нехай голку кинуто п разів і т разів вона перетнула пряму. При досить великих п віднось Тому при досить великих п відносна частота
Під час проведення випробувань голку було кинуто 5000 разів, причому найближчу пряму вона перетнула 2532 рази. Довжина голки була 36 мм, відстань між паралельними прямими 45 мм. Отже,
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.72.11 (0.007 с.) |


 (1)
(1)


 , 0<у<а. Оскільки з ΔACBD = ВС = ABsinx = lsinx, то голка перетне пряму тільки тоді, коли у < d, тобто
, 0<у<а. Оскільки з ΔACBD = ВС = ABsinx = lsinx, то голка перетне пряму тільки тоді, коли у < d, тобто (2)
(2) . Площа заштрихованої фігури
. Площа заштрихованої фігури

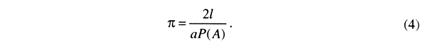
 як завгодно мало відрізняється від імовірності Р(А). Тому
як завгодно мало відрізняється від імовірності Р(А). Тому