
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление комплексных чиселСодержание книги Поиск на нашем сайте
Алгебраическая форма Запись комплексного числа z в виде x + iy, Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i 2 = − 1): (a + ib) + (c + id) = (a + c) + i (b + d);
Тригонометрическая и показательная формы Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент z = r (cos φ + i sin φ). Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера: z = rei φ, где ei φ — расширение экспоненты для случая комплексного показателя степени. Отсюда вытекают следующие широко используемые равенства:
Формула Муавра и извлечение корней из комплексных чисел Основная статья: Формула Муавра
Корни пятой степени из единицы (вершины пятиугольника) Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид: zn = [ r (cos φ + i sin φ)] n = rn (cos n φ + i sin n φ), где r — модуль, а Аналогичная формула применима также и при вычислении корней n -ой степени из ненулевого комплексного числа: z 1 / n = [ r (cos(φ + 2π k) + i sin(φ + 2π k))]1 / n =
Отметим, что корни n -й степени из ненулевого комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n -угольника, вписанного в окружность радиуса ТЕМА 1. Векторная алгебра Основные понятия Определение. Множеством называется совокупность объектов любой природы, которые объединены в одну группу (систему, совокупность) по тем или иным признакам (множество городов, множество положительных чисел, множество студентов, множество действительных чисел и т.д.).
2. Действия над n -мерными векторами Пусть даны векторы
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.35.129 (0.01 с.) |

 , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.
 (x = r cos φ, y = r sin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме
(x = r cos φ, y = r sin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме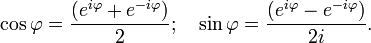




 с центром в начале координат (см. рисунок).
с центром в начале координат (см. рисунок). є U и
є U и  є U определены операция сложения:
є U определены операция сложения:  и операция умножения любого элемента на число:
и операция умножения любого элемента на число:  , удовлетворяющие свойствам:
, удовлетворяющие свойствам: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,  – нулевой элемент
– нулевой элемент  , а коэффициенты α, β, λ, 1 – действительные числа.
, а коэффициенты α, β, λ, 1 – действительные числа. , где
, где 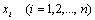 - координаты вектора. Размерность вектора определяется числом его координат и является его отличительной характеристикой. Векторы равны, если они одной размерно-сти и имеют равные соответствующие координаты: (2,3,5) = (2,3,5). Нуль-вектор
- координаты вектора. Размерность вектора определяется числом его координат и является его отличительной характеристикой. Векторы равны, если они одной размерно-сти и имеют равные соответствующие координаты: (2,3,5) = (2,3,5). Нуль-вектор  = (0,0,…,0) не следует путать с числом нуль.
= (0,0,…,0) не следует путать с числом нуль. , а соответствующие цены – вектором
, а соответствующие цены – вектором  .
. и
и  .
. называется вектор
называется вектор  , т.е. при сложении векторов их соответствующие координаты складываются: (2, –4) + (–2, 4) = (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5).
, т.е. при сложении векторов их соответствующие координаты складываются: (2, –4) + (–2, 4) = (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5). называется вектор
называется вектор  т.е. при умножении вектора на число каждая его координата умножается на это число.
т.е. при умножении вектора на число каждая его координата умножается на это число. и
и  называется число, равное сумме произведений соответствующих координат векторов:
называется число, равное сумме произведений соответствующих координат векторов: 
 и
и  .
. .
. , причем
, причем  , только при
, только при 
 ,
,  ,
,  .
. .
. Тогда
Тогда  ортогональны.
ортогональны.


