
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка выборочных показателей связи
Если корреляционная связь исследуется на основе выборочных данных, то требуется статистическая оценка полученных результатов. Статистическая оценка включает в себя, во первых, проверку гипотезы о существенности (отсутствии) связи, а во-вторых, установлении границ того или иного показателя связи в генеральной совокупности. Во- первых, следует проверить гипотезу о существенности уравнения в целом. Эта гипотеза проверяется на основе критерия F – Фишера, фактическое значение которого определяется как отношение дисперсий Фактически значения критерия сравниваются с табличным, при этом, если используется критерий:t-нормального распределения, табличное значение зависит только от уровня значимости, если же используется критерий t-Стьюдента, то его табличное значение кроме уровня значимости зависит от числа степеней свободы, которое равно
Тема №10 Корреляционная зависимость между уровнями взаимосвязанных рядов динамики. При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней 2-х или более рядов динамики различного содержания, но связанных между собой. Эта задача решается методами коррелирования: 1. уровней ряда динамики 2. отклонений фактических уровней от тренда 3. последовательных разностей Коррелирование уровней динамических рядов с применением парного коэффициента корреляции правильно показывает тесноту связи лишь в том случае, если в каждом из них отсутствует автокорреляция. Наличие зависимости между последующими и предшествующими уровнями динамического ряда в статистической литературе называют автокорреляцией. Поэтому прежде, чем коррелировать ряды динамики по уровням, необходимо проверить каждый из рядов на наличие или отсутствие в них автокорреляции. Применение методов классической теории корреляции в динамических рядах связано с некоторыми особенностями. Прежде всего, это наличие для большинства динамических рядов зависимости последующих уровней от предыдущих. Коэффициент автокорреляции вычисляется по непосредственным данным рядов динамики, когда фактические уровни одного ряда рассматриваются как значения факторного признака, а уровни этого же ряда со сдвигом на один период, принимаются в качестве результативного признака (этот сдвиг называется лагом). Коэффициент автокорреляции рассчитывается на основе формулы коэффициента корреляции для парной зависимости:
где yt– фактические уровни ряда, а yt+1 – уровни того же ряда со сдвигом на 1 период (коэффициент автокорреляции первого порядка). Примечание: во избежание путаницы, следует обратить внимание на порядок, по которому будет производиться сдвиг уровней, а именно, вниз или вверх. Соответственно и в формулах по разным источникам, ряд со сдвигом отображают либо так y t-1 либо y t+1 Формула для расчета коэффициента автокорреляции уровней ряда 1-го порядка:
Формула для расчета коэффициента автокорреляции уровней ряда 2-го порядка:
Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду, фактическое значение коэффициента автокорреляции сопоставляют с табличным для 5% или 1% уровня значимости (т. е. по величине вероятности допустить ошибку при принятии гипотезы о независимости уровней ряда). Если расчетное значение меньше табличного, то гипотеза об отсутствии автокорреляции принимается и, наоборот, в противном случае, отвергается. Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции) называют коррелограммой. Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты. Так, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденци ю. Если наиболее высоким оказался коэффициент автокорреляции порядка m, то ряд содержит циклические колебания с периодичностью в m моментов времени. Если же ни один из коэффициентов автокорреляции не является значимым, то можно сделать одно из двух предположений: 1. либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой; 2. либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Необходимо подчеркнуть, что линейные коэффициенты автокорреляции характеризуют тесноту только линейной связи текущего и предыдущих уровней ряда. Поэтому, по коэффициентам автокорреляции можно судить только о наличии или отсутствии линейной зависимости (или близкой к линейной). Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако, при этом могут иметь убывающую тенденцию. Для проверки ряда на наличие нелинейной тенденции рекомендуется вычислить линейные коэффициенты автокорреляции для временного ряда, состоящего из логарифмов исходных уровней. Отличные от нуля значения коэффициентов автокорреляции будут свидетельствовать о наличии нелинейной тенденции.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.66.206 (0.009 с.) |
 Для нахождения необходимых дисперсий соответствующие объемы вариации (
Для нахождения необходимых дисперсий соответствующие объемы вариации ( и
и  ) следует разделить на их число степеней свободы
) следует разделить на их число степеней свободы  , где m- число параметров уравнения;
, где m- число параметров уравнения;  , где n- число наблюдений на основе которых построено уравнение связи. Полученное фактическое значение критерия сравнивается с табличным (
, где n- число наблюдений на основе которых построено уравнение связи. Полученное фактическое значение критерия сравнивается с табличным (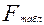 ), которое зависит от уровня значимости и числа степеней свободы воспроизведенной и остаточной вариации. Если
), которое зависит от уровня значимости и числа степеней свободы воспроизведенной и остаточной вариации. Если  принимается гипотеза о несущественности уравнения и дальнейшая оценка показателей связи не требуется, если же
принимается гипотеза о несущественности уравнения и дальнейшая оценка показателей связи не требуется, если же  принимается гипотеза о существенности уравнения и требуется дальнейшая оценка показателей связи. Проверка гипотезы относительно выборочных коэффициентов регрессии и корреляции осуществляется на основе двух критериев:t-нормального распределения, если численность выборки превышает 30 единиц или критерия t-Стьюдента при численности выборки равной или меньше 30 единиц. В качестве нулевой гипотезы выдвигаются предположения, что в генеральной совокупности коэффициенты регрессии (или корреляции) равны О (В=0 или R=0), в качестве альтернативной - в генеральной совокупности эти коэффициенты нулю не равны (В
принимается гипотеза о существенности уравнения и требуется дальнейшая оценка показателей связи. Проверка гипотезы относительно выборочных коэффициентов регрессии и корреляции осуществляется на основе двух критериев:t-нормального распределения, если численность выборки превышает 30 единиц или критерия t-Стьюдента при численности выборки равной или меньше 30 единиц. В качестве нулевой гипотезы выдвигаются предположения, что в генеральной совокупности коэффициенты регрессии (или корреляции) равны О (В=0 или R=0), в качестве альтернативной - в генеральной совокупности эти коэффициенты нулю не равны (В  ≠ 0 или R≠ 0).
≠ 0 или R≠ 0).  , где
, где 
 - выборочный коэффициент регрессии.
- выборочный коэффициент регрессии.  - средняя ошибка коэффициента регрессии, которая рассчитывается по формуле
- средняя ошибка коэффициента регрессии, которая рассчитывается по формуле  , где
, где  - остаточная вариация результативного признака;
- остаточная вариация результативного признака;  - объем вариации факторного признака;2) для коэффициента корреляции
- объем вариации факторного признака;2) для коэффициента корреляции  , где
, где  , при этом r- выборочный коэффициент корреляции
, при этом r- выборочный коэффициент корреляции , где n –число наблюдений, m- число параметров уравнения. Принятие решения о справедливости нулевой или альтернативной гипотез осуществляется по традиционной, ранее изложенной схеме. Если была принята альтернативная гипотеза о существенности показателей связи, следует найти границы этих показателей в генеральной совокупности.: для коэффициента регрессии: В = b ±
, где n –число наблюдений, m- число параметров уравнения. Принятие решения о справедливости нулевой или альтернативной гипотез осуществляется по традиционной, ранее изложенной схеме. Если была принята альтернативная гипотеза о существенности показателей связи, следует найти границы этих показателей в генеральной совокупности.: для коэффициента регрессии: В = b ±  , где
, где  а для коэффициента корреляции его границы в генеральной будут такими R= r ±
а для коэффициента корреляции его границы в генеральной будут такими R= r ±  , где
, где 






