Интерпретация коэффициентов уравнения связи

Раскроем содержание полученных коэффициентов уравнения. Если подойти формально математически, то коэффициент а – это значение результативного признака у при х=0. Однако любое уравнение корреляции строится,как уже говорилось, на основе некоторых эмпирических данных, поэтому а – это у при х=0 лишь в том случае если факторный признак х принимает или может принять это значение. Иными словами прежде чем интерпретировать а надо определить так называемую область существования корреляционного уравнения связи. 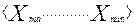Область существования корреляционного уравнения связи ограничивается максимальным и минимальным значениями факторного признака Если Х=0 входит в область существования, только в этом случае можно говорить, что а – это значение результативного признака у при х=0. Если же Х=0 находится вне области существования, то а является неким условным началом и содержательной интерпретации не подлежит. Коэффициент в получил название коэффициента регрессии. Он показывает (в случае линейной связи) на сколько в среднем изменится результативный признак при изменении факторного на единицу. Если изучается связь между двумя признаками (один результативный, другой факторный), то такая корреляция носит название парной и коэффициент в в этом случае называется коэффициентом полной регрессии, который отражает влияние фактора, игнорируя то обстоятельство, что влияние могут оказывать и другие факторы. Если изучается связь результативного признака с несколькими факторами, то такая корреляция называется множественной и коэффициенты () в уравнении получили название коэффициентов чистой регрессии, которые показывают насколько в среднем изменится величина результативного признака при изменении соответствующего фактора на 1, при условии, что влияние других факторов включенных в уравнение учтено.

Коэффициенты регрессии являются величинами именованными, имя их определяется именами результативного и факторного признаков. Вследствие сказанного, коэффициенты чистой регрессии между собой не сопоставимы. Сопоставимы между собой стандартизированные коэффициенты регрессии: - коэффициенты (бета- коэффициенты) и коэффициенты эластичности. Алгоритмы их расчета следующие: :, где - бета – коэффициент по i- му фактору; - коэффициент чистой регрессии по этому фактору; 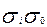- средние квадратические отклонения соответственно по i-ому факторному признаку и признаку результативному; Эi = 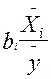, где Эi- коэффициент эластичности по i –ому фактору, - коэффициент регрессии по по i –ому фактору, средние значения соответственно по i –ому фактору и результативному признаку. - бета – коэффициент показывает насколько своих средних квадратических отклонений в среднем изменится результативный признак при изменении соответствующего фактора на свое среднее квадратическое отклонение. Коэффициент эластичности показывает на сколько долей (процентов) в среднем изменится результативный признак при изменении соответствующего фактора на долю (процент). По величине стандартизированных коэффициентов регрессии можно судить о степени влияния соответствующего фактора на результат.