
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Моделювання та оптимізація ризикуСодержание книги
Поиск на нашем сайте
1. Функція ризику. 2. Критерії прийняття рішень при заданому розподілі ймовірностей. 3. Критерії прийняття рішень, коли невідомий розподіл ймовірностей. 4. Критерії прийняття рішень у ситуації, що характеризується антагоністичними інтересами середовища. 5. Шоста інформаційна ситуація. 1. Функція ризику. Для дослідження статистичних моделей за умов ризику та невизначеності виходять із схеми, що передбачає наявність: - у суб’єкта керування – множини взаємовиключаючих рішень Х = {х1, х2, …, хм}, одне з яких йому необхідно прийняти; - множини взаємовиключаючих станів економічного середовища, однак, суб’єктові керування невідомо, у якому стані буде знаходитись середовище; - у суб’єкта керування – функціонал оцінювання F = {fkj}, що характеризує “виграш” чи “програш” під час вибору рішення хк Творча складова прийняття рішень за умов ризику має вирішальне значення. Формальна складова процесу прийняття рішення за умов невизначеності полягає у проведенні розрахунків, за існуючими алгоритмами, показників ефективності, що входять у визначення функціоналу оцінювання F={fkj}, та розрахунків для знаходження оптимального розв’язку х* Функціонал оцінювання F має позитивний інгредієнт, якщо намагається досягнути
Для таких випадків записують F=F+={fkj+}. Для негативного інгредієнта, якщо намагаються досягнути відповідно записують
F=F -={f -kj}. Визначення функціоналу оцінювання у формі F=F+, як правило, використовується для оптимізації категорії корисності, виграшу, ефективності, ймовірності досягнення цільових подій, тощо. У формі F=F - - використовують для оптимізації збитків, ризику, тощо. Так звана функція ризику визначається як лінійне перетворення позитивно чи негативно заданого інгредієнта функціоналу оцінювання до відносних одиниць вимірювання. Таке перетворення встановлює початок відліку функціоналу оцінювання для кожного стану економічного середовища Øj 1) для F+,коли мають зафіксований стан середовища Øj lj = функція ризику визначається у виді rkj = rj(xk) = lj – f 2) для F -, при фіксованих Øj Lj = функція ризику визначається у вигляді rkj = rj(xk) = f 2. Критерії прийняття рішень при заданому розподілі ймовірностей Спочатку дамо визначення інформаційної ситуації. Під інформаційною ситуацією J розуміють певний ступінь градації невизначеності вибору середовищем своїх станів у момент прийняття рішення. За класифікатором інформаційних ситуацій, пов’язаних з невизначеністю середовища, виділяють шість інформаційних ситуацій: · J1 – характеризується заданим розподілом апріорних ймовірностей на елементах множини Ø; · J2 – характеризується заданим розподілом ймовірностей з невідомими параметрами; · J3 – характеризується заданою системою лінійних співвідношень на компонентах апріорного розподілу станів середовища; · J4 – характеризується невідомим розподілом ймовірностей на елементах множини Ø; · J5 – характеризуються антагоністичними інтересами середовища у процесі прийняття рішень; · J6 – характеризуються як проміжні між J1 та J5 при виборі середовища своїх станів. Отже, перша інформаційна ситуація J1 має місце тоді, коли мають апріорний розподіл ймовірностей P= (p1, p2, …, pj), pj = p (Ø=Øj), Ця ситуація є, мабуть, найбільш розповсюдженою в більшості практичних задач прийняття рішень за умов ризику. При цьому ефективно використовуються конструктивні методи теорії ймовірностей та математичної статистики. Розглянемо один із критеріїв прийняття рішень у цій ситуації. Критерій Байєса Суть критерію – максимізація математичного сподівання функціоналу оцінювання. Назва критерію пов’язана з перетворенням формул апріорних ймовірностей у апостеріорні. Критерій Байєса часто називають критерієм середніх (сподіваних) затрат (критерієм ризику при F=F -). Згідно з критерієм Байєса оптимальними розв’язками х
Якщо максимум досягається на декількох рішеннях з х, множину яких позначимо через Величина Якщо функціонал оцінювання задано у формі F -, то замість оператора max математичного сподівання використовується min математичного сподівання. Якщо функціонал оцінювання задано в ризиках, то сподівану величину B- (xk,p) називають байєсівським ризиком для розв’язку xk У першій інформаційній ситуації J1 при прийняті рішень за умов ризику користуються апріорними ймовірностями.
3. Критерії прийняття рішень, коли невідомий розподіл ймовірностей Інформаційна ситуація J4 характеризується невідомим розподілом P=(p1,…, pn), pj= P{Ø=Øj}, На практиці такі ситуації виникають, коли впроваджуються на підприємствах зразки нової техніки, коли мова йде про реалізацію нових зразків товарів народного споживання, коли зовсім невідомий попит, а також при відпрацюванні у виробництві нових технологічних способів, транспортних маршрутів тощо. Критерій Бернуллі-Лапласа В основу цього критерію покладено відомий “принцип недостатніх підстав”. Він вперше був сформульований Бернулі і в загальних рисах означає: якщо немає даних для того, щоб вважати один стан середовища з множини Ø більш ймовірним, ніж будь-який інший стан середовища з множини Ø, то апріорні ймовірності pj станів середовища треба вважати рівними, тобто згідно з принципом недостатніх підстав точкові оцінки визначаються так
Ці оцінки розподілу апріорних ймовірностей дозволяють застосовувати критерії першої інформаційної ситуації J1. Критерій Бернуллі-Лапласа, що ґрунтується на застосуванні критерію Байєса та принципу недостатніх підстав для одержання оцінок апріорних ймовірностей pj, формулюється таким чином. Оптимальним згідно з критерієм Бернуллі-Лапласа є те рішення
Таким чином, можливі стани розглядаються як рівноймовірні, якщо немає жодних відомостей про умови, за яких кожний стан може відбутися. Домінування розв’язку хк над розв’язком хi можна гарантувати у тому і лише в тому випадку, коли
Тому необхідною і достатньою умовою пріоритету розв’язку хк з множини Х є використання нерівності
Принцип максимуму Гіббса-Джейнса Згідно з принципом Гіббса-Джейнса найбільш характерними розподілами ймовірностей станів невизначеного середовища є такі розподіли, котрі максимізують вибрану міру невизначеності при заданий інформації щодо поводження середовища. Тут використовується формалізм відтворення невідомих законів розподілу випадкової величини за наявності обмежень з умов максимуму ентропії Шеннона:
Необхідно зазначити, що Н(р) являє собою міру невизначеності, що знаходиться з розподілу апріорних ймовірностей р станів середовища. Формалізм Джейнса постулює: найменш сумнівним розподілом ймовірностей буде такий, що максимізує невизначеність при врахуванні всієї заданої інформації. Застосування принципу максимальної невизначеності Гіббса-Джейнса за умов інформаційної ситуації J4 дозволяє визначити точкову оцінку з умов
у виді Суттєвою перевагою принципу максимальної невизначеності Гіббса-Джейнса є те, що існує можливість одержання оцінок апріорного розподілу, в яких суб’єктом керування можуть бути накладені обмеження на розподіл апріорних ймовірностей станів середовища, наприклад, у формі задання середніх та дисперсій (ризику) характеристик значень функціоналу оцінювання F.
4. Критерії прийняття рішень у ситуації, що характеризується антагоністичними інтересами середовища Критерій Вальда На відміну від “пасивного” середовища чи середовища, стан якого реалізується згідно з заданим розподілом ймовірностей, активне середовище прагне до вибору таких станів з множини Ø, для котрих функціонал оцінювання F=F+ приймає мінімальне значення з множини своїх можливих значень. Основною тенденцією для суб’єкта керування буде при цьому забезпечення собі гарантованих (максимінних) рівнів значень функціоналу оцінювання, тобто зведення ризику до нуля. Таким чином, у ситуації J5 невизначеність цілком обумовлена тим, що суб’єктові керування невідомо, в якому стані з множини Ø знаходиться економічне середовище. У теоретичній моделі ступінь невизначеності зменшений через припущення, що економічне середовище активно протидіє досягненню найбільшої ефективності рішень, що приймаються, шляхом вибору таких своїх станів, які зводять до мінімуму максимальну ефективність процесу управління. Коли F=F+, то згідно з принципом максиміну кожному рішенню хк
Оптимальним називають таке рішення
Тобто, критерій Вальда ґрунтується на максимінному принципі для F=F+, що полягає у прийнятті такого рішення
Критерій мінімального ризику Севіджа Цей критерій був запропонований у 1951 році і на даний час є одним із основних критеріїв, що задовольняє принципові мінімаксу. У критерії Севіджа функціонал оцінюється вираженням у формі ризику F=F -. Згідно з цим критерієм оптимальним рішенням
Доречним обмеженням у критерії Севіджа є обмеження виду
5. Шоста інформаційна ситуація Інформаційна ситуація J6 визначається наявністю факторів, що характеризують два типи “проміжної” поведінки середовища. Для першого типу характерна наявність у суб’єкта керування деякої “неясної” інформації щодо дійсних розподілів стану середовища. Якою б “неясною” інформація не була, суб’єкт керування хоч і не може постулювати яку-небудь конкретну інформаційну ситуацію Ji(i= Для другого типу вважається, що суб’єкт керування має інформацію про стан середовища, яка є “проміжною” між інформаційними ситуаціями J1 та J5, тобто для цього випадку така інформаційна ситуація знаходиться між двома крайніми ситуаціями J1 та J5, що характеризуються, з одного боку, повним або частковим знанням щодо розподілів ймовірностей на Ø, а з другого – антагоністичною поведінкою середовища. Критерій Гурвіца Критерій Вальда та Севіджа песимістичні в тому розумінні, що з кожним рішенням вони поєднують стан середовища, що призводить до гарантованих (безризикових) наслідків для прийнятого суб’єктом керування рішення. Але можна спробувати врахувати поводження середовища, що вважається для суб’єкта керування зваженою комбінацією найкращого та найгіршого. Такий підхід до вибору критерію прийняття рішення, відомий як критерій показника песимізму – оптимізму, був вперше запропонований Гурвіцем. Особливістю цього критерію є те, що він передбачає не повний антагонізм середовища, а лише частковий. Сутність критерію Гурвіца полягає в знаходженні оптимального рішення
при фіксованому
то для фіксованого Критерій Ходжеса-Лемана Ходжес та Леман стверджують, що в практиці прийняття рішень за умов невизначеності інформації щодо стану середовища часто знаходиться між повним незнанням та точним знанням апріорного розподілу. Критерій Ходжеса-Лемана дозволяє використати можливу інформацію, яку має суб’єкт керування, але в той самий час забезпечує заданий рівень гарантії у випадку, коли ця інформація неточна. В деякому розумінні критерій Ходжеса-Лемана являє собою “суміш” критеріїв Байєса та Вальда.
|
||||
|
Последнее изменение этой страницы: 2017-01-28; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.181 (0.01 с.) |

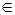 Х, якщо середовище знаходиться (буде знаходитися) у стані Øj
Х, якщо середовище знаходиться (буде знаходитися) у стані Øj  (5.1)
(5.1) , (5.2)
, (5.2) ; j=
; j=  ; k=
; k=  ; (5.3)
; (5.3)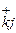 ; j=
; j=  ; j=
; j=  - Lj; j=
- Lj; j= 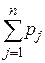 =1 на елементах Øj
=1 на елементах Øj 

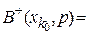
 . (5.7)
. (5.7) , то такі рішення називають еквівалентними.
, то такі рішення називають еквівалентними. називається байєсівським значенням функціоналу оцінювання для рішення
називається байєсівським значенням функціоналу оцінювання для рішення  . Критерій Байєса є найбільш розповсюдженим в інформаційній ситуації J1. Цей критерій тісно пов’язаний з аксіомами теорії корисності (аксіома Неймана та Моргенштерна), де сумарна сподівана корисність визначається як математичне сподівання корисностей окремих результатів.
. Критерій Байєса є найбільш розповсюдженим в інформаційній ситуації J1. Цей критерій тісно пов’язаний з аксіомами теорії корисності (аксіома Неймана та Моргенштерна), де сумарна сподівана корисність визначається як математичне сподівання корисностей окремих результатів. .
.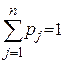 на елементах Ø, з одного боку, та відсутністю активної протидії середовища цілям щодо прийняття рішень суб’єктом керування з іншого. Поводження “пасивної природи”, що досліджується у теорії статистичних рішень, та середовища співпадає. Інакше кажучи, ситуація J4 характеризується цілковитим незнанням суб’єктом керування про те, що стосується ймовірності поводження середовища.
на елементах Ø, з одного боку, та відсутністю активної протидії середовища цілям щодо прийняття рішень суб’єктом керування з іншого. Поводження “пасивної природи”, що досліджується у теорії статистичних рішень, та середовища співпадає. Інакше кажучи, ситуація J4 характеризується цілковитим незнанням суб’єктом керування про те, що стосується ймовірності поводження середовища. . (5.8)
. (5.8) , де
, де (5.9)
(5.9) (5.10)
(5.10)
 0 (5.11)
0 (5.11) (5.12)
(5.12)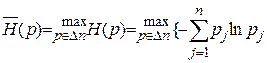 (5.13),
(5.13), . (5.14)
. (5.14) , для якого
, для якого . (5.15)
. (5.15) , яке задовольняє умові
, яке задовольняє умові . (5.16)
. (5.16) (5.17)
(5.17) для усіх хк
для усіх хк 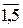 ), але може встановити деякий рівень песимізму - оптимізму.
), але може встановити деякий рівень песимізму - оптимізму.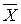 ), для якого виконується умова
), для якого виконується умова (5.19)
(5.19) . Якщо позначити
. Якщо позначити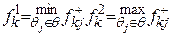 , (5.20)
, (5.20) , який будемо називати
, який будемо називати 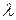 показником Гурвіца рішення
показником Гурвіца рішення 


