
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первичная обработка результатов измеренийСтр 1 из 4Следующая ⇒
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Предметом математической статистики является изучение методов сбора, систематизации и обработки экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений. К основным задачам математической статистики относятся следующие: 1) задача нахождения неизвестного закона распределения СВ по статистическим данным; 2) задача нахождения неизвестных параметров распределения или числовых характеристик СВ; 3) задача проверки правдоподобия гипотез о законах или параметрах распределения СВ.
ПЕРВИЧНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ Выборка и её вариационный ряд. Гистограмма и полигон частот
Пусть Х – непрерывная СВ, результаты измерений которой представлены в виде статистического ряда, т.е. построены интервалы Полигоном частот называется функция
Таким образом, график полигона
Пусть теперь Х – дискретная СВ, результаты измерений которой представлены в виде статистического ряда, т.е. определены различные элементы выборки
ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ Точечные оценки математического ожидания, дисперсии Получение точечных оценок методом максимального Правдоподобия. Оценки параметров распределения Пуассона И нормального распределения
Пусть
где
где Построив функцию правдоподобия L, нужно найти такие функции Поскольку максимумы функций L и Пусть генеральная совокупность Х имеет распределение Пуассона. Тогда функция правдоподобия имеет вид
Для нахождения функции Пусть, далее, генеральная совокупность Х имеет нормальное распределение. Тогда функция правдоподобия имеет вид
Переходя к логарифмической функции правдоподобия
и решая систему уравнений
относительно m и s, находим
Критерий согласия Пирсона
Критерий Пирсона используется для проверки гипотезы о предполагаемом законе распределения генеральной совокупности Х по данным выборки Множество возможных значений СВ Х разбивается на l непересекающихся интервалов (в случае непрерывной СВ) или l групп различных значений (в случае дискретной СВ). Далее по данным сформированной выборки
где l – число интервалов (групп значений), n – объём выборки, Если гипотеза является истинной, то статистика К при бесконечно большом n независимо от закона распределения СВ Х имеет распределение “хи-квадрат” с При использовании критерия предполагается, что Для принятия или отклонения гипотезы задаётся уровень значимости a и с помощью таблицы определяется значение Основное достоинство критерия Пирсона состоит в возможности определять значения параметров предполагаемого закона распределения по данным выборки. Основной недостаток критерия состоит в том, что при его использовании происходит потеря информации из-за группировки элементов выборки по интервалам или группам значений.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Предметом математической статистики является изучение методов сбора, систематизации и обработки экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений. К основным задачам математической статистики относятся следующие: 1) задача нахождения неизвестного закона распределения СВ по статистическим данным; 2) задача нахождения неизвестных параметров распределения или числовых характеристик СВ; 3) задача проверки правдоподобия гипотез о законах или параметрах распределения СВ.
ПЕРВИЧНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.172.68 (0.015 с.) |
 ,
,  и найдены частоты
и найдены частоты  ,
, 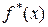 , которая на каждом из интервалов
, которая на каждом из интервалов 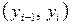 принимает значение
принимает значение 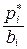 , где
, где 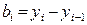 есть длина соответствующего интервала. При
есть длина соответствующего интервала. При 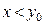 и
и 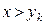 полагается
полагается 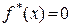 . Площадь ступенчатой фигуры под графиком
. Площадь ступенчатой фигуры под графиком 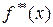 , графиком которой является ломаная, последовательно соединяющая точки
, графиком которой является ломаная, последовательно соединяющая точки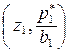 ,
, 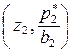 ,...,
,..., 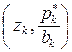 .
.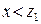 и
и 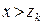 полагается
полагается 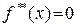 . При большом объёме выборки гистограмма и полигон частот используются в качестве оценки плотности распределения
. При большом объёме выборки гистограмма и полигон частот используются в качестве оценки плотности распределения 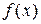 СВ Х.
СВ Х. , расположенные в порядке возрастания, и соответствующие им частоты
, расположенные в порядке возрастания, и соответствующие им частоты 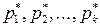 . Тогда полигоном частот называется функция
. Тогда полигоном частот называется функция 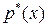 , графиком которой является ломаная, последовательно соединяющая точки
, графиком которой является ломаная, последовательно соединяющая точки 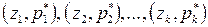 . При большом объёме выборки полигон частот служит статистическим аналогом многоугольника распределения.
. При большом объёме выборки полигон частот служит статистическим аналогом многоугольника распределения.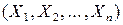 – случайная выборка объёма n из генеральной совокупности Х, закон распределения которой зависит от некоторых параметров
– случайная выборка объёма n из генеральной совокупности Х, закон распределения которой зависит от некоторых параметров  . Если Х – дискретная СВ, то функцией правдоподобия случайной выборки называется
. Если Х – дискретная СВ, то функцией правдоподобия случайной выборки называется ,
, есть вероятность события
есть вероятность события  , зависящая от значения аргумента
, зависящая от значения аргумента  и от значений параметров
и от значений параметров 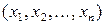 . Если Х – непрерывная СВ, то
. Если Х – непрерывная СВ, то ,
, есть плотность распределения СВ Х, зависящая от значений параметров
есть плотность распределения СВ Х, зависящая от значений параметров  ,
,  , в результате подстановки которых вместо соответствующих аргументов
, в результате подстановки которых вместо соответствующих аргументов  функция L при любых значениях аргументов
функция L при любых значениях аргументов  принимает максимальное значение. Пользуясь необходимым условием экстремума, для этого следует решить систему уравнений
принимает максимальное значение. Пользуясь необходимым условием экстремума, для этого следует решить систему уравнений  ,
,  ,
,  на
на  и
и  на
на  , получим искомые оценки.
, получим искомые оценки. достигаются при одних и тех же значениях аргументов, то для удобства вместо функции правдоподобия L обычно используется логарифмическая функция правдоподобия
достигаются при одних и тех же значениях аргументов, то для удобства вместо функции правдоподобия L обычно используется логарифмическая функция правдоподобия  ,
, 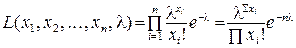 .
.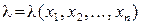 , при которой L обращается в максимум, перейдём к логарифмической функции правдоподобия
, при которой L обращается в максимум, перейдём к логарифмической функции правдоподобия  Решив уравнение
Решив уравнение  относительно l, найдём
относительно l, найдём  , т.е. искомая оценка параметра l имеет вид
, т.е. искомая оценка параметра l имеет вид 
 .
.
 ,
, 
 ,
,  , т.е. оценки параметров имеют вид
, т.е. оценки параметров имеют вид 
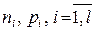 , где
, где  – количество элементов выборки, попавших в i -й интервал (i -ю группу значений),
– количество элементов выборки, попавших в i -й интервал (i -ю группу значений), 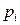 – вероятность попадания СВ Х в i -й интервал (i -ю группу значений), вычисленная для предполагаемого закона распределения. После этого вычисляется значение статистики
– вероятность попадания СВ Х в i -й интервал (i -ю группу значений), вычисленная для предполагаемого закона распределения. После этого вычисляется значение статистики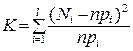 ,
,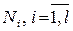 – СВ, реализацией которых являются соответствующие значения
– СВ, реализацией которых являются соответствующие значения 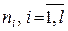 .
.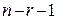 степенями свободы, где r – количество параметров закона распределения, значения которых определяются по данным выборки. Если, например, выдвинута гипотеза о согласии статистических данных с нормальным распределением (или с распределением Пуассона), но соответствующие параметры m и s (или параметр l) не заданы и в качестве их значений используются реализации точечных оценок, то следует положить
степенями свободы, где r – количество параметров закона распределения, значения которых определяются по данным выборки. Если, например, выдвинута гипотеза о согласии статистических данных с нормальным распределением (или с распределением Пуассона), но соответствующие параметры m и s (или параметр l) не заданы и в качестве их значений используются реализации точечных оценок, то следует положить 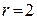 (или
(или 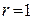 ). Если выдвинута гипотеза о согласии с заданным законом распределения с заданными значениями параметров, то
). Если выдвинута гипотеза о согласии с заданным законом распределения с заданными значениями параметров, то 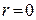 .
.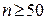 и разбиение на интервалы или группы значений проведено так, что
и разбиение на интервалы или группы значений проведено так, что 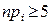 ,
, 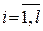 . Рекомендуется брать
. Рекомендуется брать 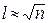 .
.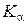 , удовлетворяющее условию
, удовлетворяющее условию 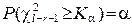 . Если вычисленное по данным выборки значение статистики К не превосходит
. Если вычисленное по данным выборки значение статистики К не превосходит 


