
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точечные оценки математического ожидания, дисперсии ⇐ ПредыдущаяСтр 4 из 4
И среднего квадратического отклонения
Пусть
При некоторых законах распределения СВ Х эта оценка является эффективной. Величина В качестве точечной оценки дисперсии может использоваться выборочная дисперсия В качестве точечных оценок среднего квадратического отклонения обычно используются величины
называемые, соответственно, выборочным и исправленным средними квадратическими отклонениями. Оценки S и Реализации оценок
Получение точечных оценок методом максимального Правдоподобия. Оценки параметров распределения Пуассона И нормального распределения
Пусть
где
где Построив функцию правдоподобия L, нужно найти такие функции Поскольку максимумы функций L и Пусть генеральная совокупность Х имеет распределение Пуассона. Тогда функция правдоподобия имеет вид
Для нахождения функции Пусть, далее, генеральная совокупность Х имеет нормальное распределение. Тогда функция правдоподобия имеет вид
Переходя к логарифмической функции правдоподобия
и решая систему уравнений
относительно m и s, находим
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.23.30 (0.009 с.) |
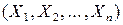 – случайная выборка из генеральной совокупности Х, математическое ожидание m и дисперсия D которой неизвестны. В качестве точечной оценки математического ожидания на практике обычно используется среднее арифметическое случайных результатов измерений, т.е. СВ
– случайная выборка из генеральной совокупности Х, математическое ожидание m и дисперсия D которой неизвестны. В качестве точечной оценки математического ожидания на практике обычно используется среднее арифметическое случайных результатов измерений, т.е. СВ 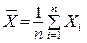 . В силу теоремы Чебышёва данная оценка является состоятельной. Она является несмещённой, т.к.
. В силу теоремы Чебышёва данная оценка является состоятельной. Она является несмещённой, т.к. .
. называется выборочным математическим ожиданием (выборочным средним).
называется выборочным математическим ожиданием (выборочным средним). , т.е. среднее арифметическое квадратов отклонений случайных результатов измерений от выборочного среднего. Доказывается, что
, т.е. среднее арифметическое квадратов отклонений случайных результатов измерений от выборочного среднего. Доказывается, что  , т.е. СВ
, т.е. СВ  является асимптотически несмещённой оценкой дисперсии. В качестве несмещённой оценки используется исправленная дисперсия
является асимптотически несмещённой оценкой дисперсии. В качестве несмещённой оценки используется исправленная дисперсия  . Оценки
. Оценки  являются состоятельными. При большом объёме выборки их реализации почти не различаются.
являются состоятельными. При большом объёме выборки их реализации почти не различаются. и
и  ,
,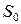 являются состоятельными и асимптотически несмещёнными.
являются состоятельными и асимптотически несмещёнными. и
и 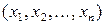 , обозначаются, соответственно,
, обозначаются, соответственно,  и
и  .
. . Если Х – дискретная СВ, то функцией правдоподобия случайной выборки называется
. Если Х – дискретная СВ, то функцией правдоподобия случайной выборки называется ,
, есть вероятность события
есть вероятность события  , зависящая от значения аргумента
, зависящая от значения аргумента  и от значений параметров
и от значений параметров  ,
, есть плотность распределения СВ Х, зависящая от значений параметров
есть плотность распределения СВ Х, зависящая от значений параметров  ,
,  , в результате подстановки которых вместо соответствующих аргументов
, в результате подстановки которых вместо соответствующих аргументов  функция L при любых значениях аргументов
функция L при любых значениях аргументов  принимает максимальное значение. Пользуясь необходимым условием экстремума, для этого следует решить систему уравнений
принимает максимальное значение. Пользуясь необходимым условием экстремума, для этого следует решить систему уравнений  ,
,  ,
,  на
на  и
и  на
на  , получим искомые оценки.
, получим искомые оценки. достигаются при одних и тех же значениях аргументов, то для удобства вместо функции правдоподобия L обычно используется логарифмическая функция правдоподобия
достигаются при одних и тех же значениях аргументов, то для удобства вместо функции правдоподобия L обычно используется логарифмическая функция правдоподобия  ,
, 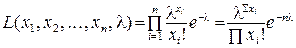 .
.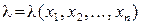 , при которой L обращается в максимум, перейдём к логарифмической функции правдоподобия
, при которой L обращается в максимум, перейдём к логарифмической функции правдоподобия  Решив уравнение
Решив уравнение  относительно l, найдём
относительно l, найдём  , т.е. искомая оценка параметра l имеет вид
, т.е. искомая оценка параметра l имеет вид 
 .
.
 ,
, 
 ,
,  , т.е. оценки параметров имеют вид
, т.е. оценки параметров имеют вид 



