Переход от стандартной и общей форм ЗЛП к канонической

Разнообразие форм задач линейного программирования затрудняет исследование их общих особенностей и создание общих методов и вычислительных алгоритмов для их решения. Рассмотрим способ сведения любой ЗЛП к наиболее простой и удобной для исследования форме — канонической.

Для осуществления перехода от стандартной формы записи к канонической нужно в каждое из m неравенств системы ограничений ввести m дополнительных неотрицательных переменных: x_n+1, x_n+2,…, x_n+m, тогда система ограничений примет вид:

a_llx₁+a₁₂x₂+... + a_1nx_n+ x_n+1 = b₁

a₂₁x₁+a₂₂x₂+ + a_2nx_n + x_n+2 = b₂ (1.5.14)

а₃₁х₁+а₃₂х₂+... + а_зnх_n + x_n+3 = b₃

_{…………………………………………}

a_m1х₁+а_m2х₂+... + а_mnх_n+ x_n+m = b_m

здесь x_n+1, x_n+2, x_n+3, …, x_n+m— выравнивающие балансовые переменные, где x_j ≥0, где (j = l,...,n+m). Добавив эти балансовые переменные в неравенства, превращаем их в уравнения. Если же в стандартной форме требовалось минимизировать целевую функцию, то, заменив ее знак на «-», получим:

F₁ = F = -c₁ х₁ - c₂ х₂ - c₃ х₃ -…..- c_n х_n → max (1.5.15)

Для решения этой задачи необходимо найти такой вектор Х=(x₁, x₂, x₃, …, x_m), который удовлетворял бы системе ограничений (1.5.14) и при котором целевая функция (1.5.15) принимала бы максимальное значение.

Пример

Пусть ЗЛП задана в стандартной форме:

F = 2х₁ + Зх₂ → max

при ограничениях:

х₁+Зх₂≤18

2x₁+x₂≤16

х₂≤5

Зх₁ ≤21

x₁≥0; х₂≥0.

Приведем эту задачу к каноническому виду. Обратим имеющуюся систему неравенств в равенства, вводя для этого в каждое из них соответствующую неотрицательную переменную:

x₁ +3х₂ + х₃ =18

2х₁ +х₂ + х₄ =16

х₂ + х₅ =5

Зх₁+ х₆ =21.

В данном примере все дополнительные переменные введены со знаком «+», так как рассматриваемые неравенства имеют знак ≤. Необходимо заметить, что в том случае, если неравенства имели бы знак ≥, переменные нужно было бы вводить со знаком «-».

Графический метод решения ЗЛП

Графический метод решения ЗЛП имеет ограниченную область применения. Как правило, этим методом решаются задачи, содержащие не более двух переменных.

Пример

Найти решение X*=(x*₁,x*₂), которое удовлетворяет системе неравенств:

a_llx₁+a₁₂x₂ ≤ b₁

a₂₁x₁+a₂₂x₂ ≤ b₂ (1.6.1)

а₃₁х₁+а₃₂х₂ ≤ b₃

_{…………………………………………}

a_m1х₁+а_m2х₂ ≤ b_m

условиям неотрицательности переменных:

х ₁ ≥ 0, х ₂ ≥ 0 (1.6.2)

и которое доставляет оптимальное значение целевой функции:

F = c₁x₁+c₂x₂ —>max(min). (1.6.3)

Применение геометрического метода предполагает использование нескольких этапов.

На первом из них в системе координат X₁OX₂ строится область допустимых решений задачи (ОДЗ). Для этого ка ждое из неравенств системы (1.6.1) заменяем равенством и строим соответствующие этим равенствам граничные прямые: a_ilx₁+a_i2x₂ = b_i (i=l,…, m).

Каждая из этих прямых делит плоскость Х₁ОХ₂ на две полуплоскости (рис. 1.6.1). Для точки (*) А, принадлежащей одной из этих полуплоскостей, выполняется неравенство: a_ilx₁+a_i2x₂ < b_i (i=l,…, m).

для любой (*)В, принадлежащей другой полуплоскости, — противоположное: a_ilx₁+a_i2x₂ > b_i (i=l...m),

а для любой из точек, лежащих на граничной прямой, — уравнение: a_ilx₁+a_i2x₂ = b_i (i=l...m).

Рис. 1.6.1. Построение ОДЗ

Чтобы графически определить, по какую сторону от граничной прямой располагается полуплоскость, содержащая решения, удовлетворяющие рассматриваемому неравенству, достаточно испытать одну какую-либо точку, например точку с координатами (0,0). Если при подстановке ее координат в левую часть неравенства оно удовлетворяется, значит, искомая полуплоскость содержит данную точку и штриховка, выделяющая искомую полуплоскость, обращена в сторону к испытуемой точке.

Если же неравенство не удовлетворяется, штриховка, выделяющая искомую полуплоскость, обращена в противоположную от данной точки сторону.

Неравенства x₁≥0 и х₂≥0 также соответствуют полуплоскостям, одна из которых расположена справа от оси ординат, а другая - над осью абсцисс (рис. 1.6.1).

Выделив полуплоскости, содержащие решения, удовлетворяющие неравенствам, входящим в рассматриваемую систему, мы определим область, в которой находятся решения, удовлетворяющие всем ограничениям, входящим в рассматриваемую систему неравенств. Именно эта область и есть область допустимых решений задачи.

Пример. Необходимо построить область допустимых решений, удовлетворяющую системе неравенств:

x₁+х₂≤ 1

x₁-x₂≤ -1

х ₁ ≥ 0, х ₂ ≥ 0

Для этого первое из неравенств обратим в равенство (x₁+х₂= 1) и построим соответствующую ему граничную прямую. Эта прямая проходит через две точки, координаты которых можно определить следующим образом. Положим, x₁=0, тогда получим 0+х₂= 1, т. е., х₂= 1,а если х₂=0, тогда x₁+0= 1, т. е.,x₁=l, следовательно, граничная прямая на рис. 1.6.2 проходит через точки с координатами (0,1) и (1,0).

Чтобы определить; в какой полуплоскости находят решения, удовлетворяющие первому неравенству, подставим точку с координатами (0,0) в первое неравенство 0+0≤ 1 и убедимся, что точка (0,0) ему удовлетворяет. Следовательно, все решения, удовлетворяющие данному неравенству, находятся в той же полуплоскости, что и точка 0, значит, штриховка, выделяющая полуплоскость, содержащую решения, удовлетворяющие первому неравенству, обращена к точке 0. Затем определим полуплоскость, в которой находятся решения, удовлетворяющие второму неравенству. Для этого второе из неравенств обратим в равенство и построим соответствующую этому равенству граничную прямую. С помощью приема, описанного выше, определим точки, через которые проходит граничная прямая; этими точками будут: (x₁=0, х₂=1) и (x₂=0, x₁=-l).

Испытав точку 0, увидим, что штриховка, выделяющая полуплоскость, содержащую решения, удовлетворяющие первому неравенству, обращена в сторону, противоположную от 0.

Выделим полуплоскости, соответствующие неравенствам: x₁ ≥ 0 и х₂ ≥ 0. Полуплоскость справа от оси ординат будет соответствовать неравенству x₁ ≥ 0, а полуплоскость над осью абсцисс — неравенству х₂ ≥ 0. В рассматриваемом примере область допустимых решений состоит из одной точки с координатами (0,1). Рис. 1.6.2. ОДЗ —одна точка

В общем случае область допустимых решений систем неравенств (1.6.1) и (1.6.2) может быть:

1. пустой, что означает несовместимость систем неравенств:

x₁+x₂≤3

x₁-x₂≤4

x₁≥0; x₂≥0

 

Рис. 1.6.3. ОДЗ —пуста

2. одной точкой:

x₁+x₂ ≤l

x₁-x₂ ≤-1

x₁ ≥0; x₂ ≥0

 

Рис. 1.6.4. ОДЗ — одна точка

3. выпуклым многоугольником:

2x₁+x₂ ≥2

x₁+3х₂ ≥3

x₁-x₂ ≥-1

Зх₁-х₂ ≤ 6

x₁+x₂ ≤ 5

x₁≥0;х₂≥0

Рис. 1.6.5. ОДЗ — выпуклый многоугольник

4. неограниченной выпуклой многоугольной областью:

Зх₁-2х₂ ≥-15

4х₁-х₂ ≥20

Зх₁+х₂ ≥30

x₁-2х₂ ≤20

х₁ ≥0;х₂ ≥0

Рис. 1.6.6. ОДЗ — неограниченная выпуклая многоугольная область

 

На втором этапе формируется графическое изображение целевой функции.

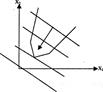
Уравнение: c₁x₁+c₂x₂ =L при фиксированном значении L определяет прямую, а при изменении L — семейство параллельных прямых с параметром L. Вектор С=(с₁,с₂), перпендикулярный всем этим прямым, показывает направление возрастания параметра L. Так, на рис. 1.6.7. показаны прямые, соответствующие уравнению 2x₁+3x₂=L при L= -3, 0, 3, 9.

 

Рис. 1.6.7. Графическое изображение целевой функции

Для всех точек, лежащих на одной из этих прямых, функция F принимает одно определенное значение, равное соответствующему значению L. Поэтому рассматриваемые прямые называются линиями уровня для параметра L. Важное свойство линии уровня в том, что при их параллельном смещении в одном направлении уровень (значение L) только возрастает, а при смещении в другом — только убывает.Построим для рассмотренного примера линии уровня и определим направление их возрастания. Чтобы построить вектор C=(c₁, с₂), можно использовать следующий прием: по оси X₁ откладывается значение первой компоненты вектора C₁=2, а по оси Х₂ — значение второй компоненты С₂=3. По найденным координатам строим прямоугольник и находим направление возрастания вектора С. Затем перпендикулярно вектору С строим линии уровня.

Рис. 1.6.8. Определение оптимального решения графическим методом

Построив на одном рисунке (рис. 1.6.8) область допустимых решений, вектор С, и перпендикулярную ему одну из линий уровня, можно путем ее параллельного перемещения в направлении, указанном вектором С (или в противоположном), определить точку в области допустимых значений, которая доставляет максимум или минимум целевой функции. На рис. 1.6.8 видно, что в крайнем положении линия уровня проходит через (*)В. При дальнейшем ее перемещении она уже не будет иметь общих точек с областью допустимых решений. Таким образом, искомое оптимальное решение, которое графически соответствует координатам (*)В, можно найти путем совместного решения системы двух уравнений, соответствующих граничным прямым АВ и ВД. Если при тех же исходных данных требовалось бы достичь минимума функции F, то, очевидно, линию уровня пришлось бы перемещать в направлении, противоположном вектору С. В этом случае оптимальное решение, соответствующее минимуму функции F, определялось бы координатами точки (*)0.

В зависимости от вида области допустимых решений и положения линий уровня возможны следующие случаи:

 

ЗЛП имеет единственное решение 1.6.10. ЗЛП имеет альтернат. оптимум (А и В)