
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формы задачи линейного программирования (ЗЛП)Содержание книги Поиск на нашем сайте
Различают три основные формы задачи линейного программирования, к которым может быть сведена любая содержательная постановка задачи. Записи целевых функций и ограничений в них существенно различаются. Ограничения могут иметь вид неравенств или равенств. Существует также ряд практических задач, в которых часть ограничений представлена в виде равенств, а часть — в виде неравенств. Общая форма задачи линейного программирования (ЗЛП) Задана система m линейных уравнений с n переменными:
a21x1+a22x2+ + a2nxn ≤ b2 (1.5.1) …………………………. аk1х1+аk2х2+... + аknхn ≤ bk аk+1,1х1+аk+1,2х2+... + аk+1,nхn = bk+1 ………………………………………… am1х1+аm2х2+... + аmnхn = bm х j ≥ 0, где j = 1,…,n (1.5.2) а линейная функция: F = (c1 х1 + c2 х2 + c3 х3 +…..+ cn хn) → max(min). (1.5.3) Необходимо найти такой вектор Х=(х1, х2, х3,…, хn), который удовлетворяет ограничениям (1.5.1) и (1.5.2) и при котором линейная функции F принимает максимальное (или минимальное) значение. Как видно из представленной выше записи, в общей форме задачи линейного программирования система ограничений (1.5.1) включает в себя как равенства, так и неравенства, а целевая функция может стремиться как к максимуму, так и к минимуму. Более кратко задачу линейного программирования в общей форме можно представить в следующем виде:
х j ≥ 0, где j = 1,…,n (1.5.7) Оптимальным решением (или оптимальным планом) задачи линейного программирования называется решение Х*=(х*1, х*2...хn), удовлетворяющее системам ограничений (1.5.5) — (1.5.7), при которых линейная функция F достигает оптимального значение (минимума или максимума). Стандартная форма задачи линейного программирования (ЗЛП) Задача линейного программирования, представленная в форме:
a21x1+a22x2+ + a2nxn ≤ b2 (1.5.8) ………………………………………… am1х1+аm2х2+... + аmnхn ≤ bm х j ≥ 0, где j=1,…,n (1.5.9) при которой целевая функция достигла бы своего max(min) значения: F = (c1 х1 + c2 х2 + c3 х3 +…..+ cn хn) → max(min) (1.5.10) называется стандартной формой задачи линейного программирования. Особенность данной формы состоит в том, что в ней система как функциональных, так и прямых ограничений состоит из одних неравенств, переменные х j, где j=l,...,n являются неотрицательными, а целевая функция может стремиться как к минимуму, так и к максимуму. Каноническая форма задачи линейного программирования (ЗЛП) Форма, в которой: F = (c1 х1 + c2 х2 + c3 х3 +…..+ cn хn) → max (1.5.11)
a21x1+a22x2+ + a2nxn = b2 (1.5.13) а31х1+а32х2+... + азnхn = b3 ………………………………………… am1х1+аm2х2+... + аmnхn = bm х j ≥ 0, где j = 1,…,n (1.5.13) все переменные х j — неотрицательны, система ограничений представляет собой систему уравнений, а целевая функция стремится к максимуму, называется канонической формой задачи линейного программирования.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.221 (0.005 с.) |

 allx1+a12x2+... + a1nxn ≤ b1
allx1+a12x2+... + a1nxn ≤ b1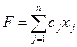 —>max(min) (1.5.4)
—>max(min) (1.5.4) , где i=1,…,k (1.5.5)
, где i=1,…,k (1.5.5)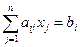 , где i=k+l,...m) (1.5.6)
, где i=k+l,...m) (1.5.6) allx1+a12x2+... + a1nxn ≤ b1
allx1+a12x2+... + a1nxn ≤ b1 allx1+a12x2+... + a1nxn = b1
allx1+a12x2+... + a1nxn = b1


