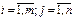Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача оптимизации: Линейное программирование, математическая модельСодержание книги
Поиск на нашем сайте
Линейное программирование представляет собой математический аппарат, разработанный для решения оптимальных задач с линейными выражениями для критерия оптимальности и линейными ограничениями на область изменения переменных. Такие задачи обычно встречаются при решении вопросов оптимального планирования производства с ограниченным количеством ресурсов, при определении оптимального плана перевозок (транспортные задачи) и т. д. Для решения большого круга задач линейного программирования имеется практически универсальный алгоритм - симплексный метод, позволяющий за конечное число итераций находить оптимальное решение подавляющего большинства задач. Тип используемых ограничений (равенства или неравенства) не сказывается на возможности применения указанного алгоритма. Дополнительной проверки на оптимальность для получаемых решений не требуется. Как правило, практические задачи линейного программирования отличаются весьма значительным числом независимых переменных. Поэтому для их решения обычно используют вычислительные машины, необходимая мощность которых определяется размерностью решаемой задачи.
qj £ xj £ Qj, где где F – целевая функция; aij, bi – постоянные коэффициенты для уравнений; cj – постоянный коэффициент для целевой функции; xj – неизвестные переменные; qj, Qj – ограничения, соответственно нижняя и верхняя границы для возможных значений xj. В процессе решения задачи необходимо определить численные значения xj, которые лежали бы в пределах от qj до Qj доставляли бы экстремум целевой функции F. Имитационное моделирование. При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы S во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы S. Все имитационные модели представляют собой модели типа «черного ящика». Это означает, что они обеспечивают выдачу выходного сигнала, если на вход системы поступает некоторый входной сигнал. Следовательно, для получения необходимой информации или результатов необходимо осуществлять прогноз имитацтонной модели, а не решать. Имитационные модели не способны формироваь свои собственные решения так, как это возможно в аналитических моделях, поэтому служат в основном в качестве средства для анализа поведения системы. Сформулируем несколько условий при которых целесообразно использовать имитационное моделирование: 1. незаконченность математического аппарата или поставленной задачи для решения этой задачи. 2. математические модели имеются, но они настолько сложны и трудоемки, что имитационное моделирование дает более простое решение задачи. 3. когда кроме определения необходимых параметров необходимо наблюдение за процессом в течение определенного периода. 4. имитационное моделирование является единственно верным средством из-за трудностей проведения эксперимента в существующих условиях.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.10.2 (0.006 с.) |

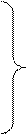 В общем виде задача линейного программирования может быть представлена следующим образом:
В общем виде задача линейного программирования может быть представлена следующим образом: