Математическое моделирование. Основные подходы к построению математических моделей систем.

Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Причем уровень абстрагирования зависит от круга тех вопросов, на которые исследователь системы хочет получить ответ с помощью модели, и в какой-то степени определяет выбор математической схемы.

Математические схемы. Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования

в виде некоторой математической модели (аналитической или имитационной). Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды. Полнота модели регулируется в основном выбором границы «система S — среда Е».

Формальная модель объекта. Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:

совокупность входных воздействий на систему

совокупность воздействий внешней среды

совокупность внутренних (собственных) параметров системы

совокупность выходных характеристик системы

При этом в перечисленных подмножествах можно выделить управляемые и неуправляемые переменные. В общем случае хi, vl, hk, yj являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие. При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, которые в векторной форме имеют соответственно вид , а выходные характеристики системы являются зависимыми (эндогенными) переменными

и в векторной форме имеют вид Процесс функционирования системы S описывается во времени оператором Fs( закон функционирования системы), который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида -соотношение 1

Весьма важным для описания и исследования системы S является понятие алгоритма функционирования As, под которым понимается метод получения выходных характеристик с учетом входных воздействий , воздействий внешней среды и собственных

параметров системы Очевидно, что один и тот же закон функционирования Fs системы S может быть реализован различными способами, т. е. с помощью множества различных алгоритмов функционирования As. Соотношения 1 являются математическим описанием поведения объекта (системы) моделирования во времени, т. е. отражают

его динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями (системами). Для статических моделей математическая модель 1 представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, Н), что в векторной форме может быть записано как (2)

Соотношения (1) и (2) могут быть заданы различными способами: аналитически (с помощью формул), графически, таблично и т. д. Такие соотношения в ряде случаев могут быть получены через свойства системы S в конкретные моменты времени, называемые

состояниями. Состояние системы 5 характеризуется векторами

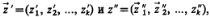
Они могут быть интерпретированы как координаты точки в fe-мерном фазовом пространстве, причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний {k} называется пространством состояний объекта моделирования Z. Состояния системы S в момент времени полностью определяются начальными условиями, входными воздействиями, внутренними параметрами и воздействиями внешней среды, которые имели место за промежуток времени t* — t0, с помощью двух векторных уравнений

(3) (4) Первое уравнение по начальному состоянию и независимым переменным х, Z, h определяет вектор-функцию, а второе по полученному значению состояний z (t) — эндогенные переменные на выходе системы у {t). Таким образом, цепочка уравнений объекта «вход — состояния — выход» позволяет определить характеристики системы 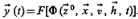(5) В общем случае время в модели системы S может рассматриваться на интервале моделирования (0, Т) как непрерывное, так и дискретное, т. е. квантованное на отрезки длиной At временных единиц каждый, когда T=mAt, где m=l, mT — число интервалов дискретизации.