
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация сущностей. Типы связей между сущностями.(IDEF 1X)Содержание книги
Поиск на нашем сайте
Сущность- описывает собой совокупность или набор экземпляров похожих по свойствам по однозначно отличаемых друг от друга по 1му или нескольким признакам. Классификация сущностей. Они делятся на зависимые и независимые: -дочерняя сущность уникальность кот зависит от атрибута уникального ключа.т.е. для этих сущностей внешний ключ является частью первичного ключа дочернего обьекта. -зависимые сущности классифицируются на сущности кот не могут существовать без родительской сущности -кот не могут быть идентифицированы без исполнения ключа родителя. -сущности не зависящие при идентификации от других обьектов в модели - независимые сущности. Типы связей. В IDEF 1X концепция зависимых и независимых сущностей усиливаются типом взаимосвязей между 2мя сущностями бывают идентифицирующ и неидентифицируемые. Неидентифицируемые связи используются для передачи атрибутов внешних ключей в область данных дочерней сущности. Преимущество IDEF 1X: является жесткое и строгое стандартизация моделирования. Устанавливаемые стандарты позволяют избежать различные трактовки построенной модели
Преимущества IDEF 1X. Основным преимуществом IDEF1X по сравнению с другими методами разраб. баз данных является жесткая и строгая стандартизация моделирования. Установленные стандарты позволяют избежать различ. трактовки построенной модели. Предназначение IDEF 3. 2 типа диаграмм. IDEF 3 явл-ся стандартом докум-ия технол-х проц-в происх-х на предприятии и представл-т “инструментарий” для наглядного исслед-я и модел-ия их сценарий. Сценарием наз. описание послед-ти измен-ий св-тв объекта в рамках рассматр-го проц-са. Исполнение кажд-го сценария сопровожд-ся соотв-им “документо-оборотом”, кот-й сост. из 2-ух осн-х потоков (это док-в опред-их струк-ру и послед-ть процесса и док-в отобра-их ход его выпол-ия). Средства док-я IDEF 3 позв. вып-ть след. зад-чи: 1Док-ть имеющ-ся данные по технол-ии проц-са, выявл-ые в проц-е опроса сотрудников ответств-ых за орг-ию рассм-го проц-са. 2Опред-ть и анализ-ть точки влияния потоков сопутствующего док-а оборота на сце-ий техн-х проц-в. 3Опред. Ситуации в кот-х треб-ся принятие реш-я влияющего на жизн-й цикл проц-са. 4Содействие принятию оптим-х реш-ий при реорганизации технол-х проц-в. 5Разраб-ть имитац-ые модели технол-х проц-в. 2 типа диаграмм: - ProcessFlowDescription…(PFDD) диагр-а описания послед-ти этапов проц-в. -ObjectStateTransition network(OSTn) диагр-а стадий обработки деталей в рамках исслед-го технол-го проц-а.
Прямоуг-ки на диагр-е наз. функц-ми эл-ми и обозн-ют стадию проц-а или принятия решения. Каждый блок имеет своё имя. Перемещение м/у блоками отобр-ся линиями: 1старше ®или ¯,®. 2отношение - - - - исп-ся для изобр-я связей м/у блоками. 3потоки объектов ®исп. для опис-я Пр:деталь или объект исп-ся в 2ух или более единицах работы. j1 перекрёсток (Function)исп. для отобр-я логики взаим-я потоков при слиянии и разветвлении или для отобр-я событий кот-е должны быть завершены перед началом след-й работы. Классификация моделей Физ. – воспроизведение постоянства определяющих критериев подобия. Физ. моделью некоторой системы наз-ют систему той же или иной природы, которая частично или полностью воспроизводить свойства исходной системы в рамках заданного приближения. Чаще всего в качестве модели исп-ся электрич. или электромагн. процессы. При этом исходные моделируемые процессы могут иметь разнообр. физ природу (мех., тепловую) Разновидностью физ. моделирования является исследование процесса той же физ. природы, но в другой области параметров (масштабные модели). Физ. моделир-е иногда является альтернативой мат. моделированию, но часто они дополняют друг друга. Мат. моделирование – качественное или количественное описание процесса с помощью мат. модели, при построении которой реальный процесс описывается с помощью того или иного мат. аппарата. Мат. модель сложного процесса, непосредственное проведение экспериментов на котором часто практически невозможно, позволяет исследовать его динамику, давая количественное описание процесса и устанавливает изменение количественного характера в динамике. Моделир. процессы разнообразные по своей природе и степени сложности. Все они делятся на детерминированные и стохастические. Детерминир-е – процессы, динамика которых полностью определяется начальными условиями и динамич. переменные являются функциями времени. Стохастические – процессы, параметры которых изменяются случайно под воздействием неконтролуируемых дестабилизирующих объектов. Поэтому однозначно предсказать поведение таких процессов на основе их изучения затруднительно. Поэтому, говорят лишь о их вероятности того или иного поведения. Мат. моделирование позволяет установить условия, при которых динамическая система переходит от детерминированного процесса к стохастическому. В соответствии с характером изучаемого процесса, строятся жесткие или вероятностные модели. Жесткие модели строятся без использования стахостич. вероятностных распределений. В этом случае определенному значению входного параметра будет соотв-ть опред. значение его выходного параметра. Связь между вх. и вых. параметрами явл-ся функциональной. Вероятностные модели описывают стох. процессы. Большинство совр. процессов носят случ. характер, когда вых. параметр связан с входным параметром статистически. В этом случае каждому определенному значению вх. параметра соотв. распределение значение вых. параметра. Поэтому вероятностные модели строятся с использованием методов теории вер-тей и мат. статистики. 17.Корреляционный анализ.Коэффициент корреляции. Корреляционное отношение Для построения матем. модели, отображаемой зависимость ф-ции оклика от фактора X Y=f(x) Стат.данные обрабатывают, подсчитывая среднее значение отклика Y для каждого определенного значения X
По виду графического изображения судят о наличии влияния одного параметра на другой.Если оно обнаружено, то говорят о наличии корреляционной связи между рассм. параметрами.
Цель корреляционного анализа – установление корреляционной связи между рассматриваемыми параметрами. Варианты: 1) X и Y связаны – зависимости обоими признаками могут выражаться в виде формулы. 2) X и Y не строго связаны – связь носит статический или вероятностный характер. 3) X и Y не связаны – связи нет.
Коэффициент корреляции:
Если Если При оценке коэффициента корреляции учитывается число пар наблюдений
Если В случае криволинейной связи между признаками оценка связи между ними осуществляется с помощью корреляционного отношения.
n – число наблюдений N – общее число наблюдений
σ – дисперсия Физическое моделирование Существует два подхода к физическому моделированию. В первом из них при изучении физики последовательно излагают физ. явления, основу которых составляют различные физ. процессы (мех., электромагнитные, ядерные и т. д.). В этом случае при физ. моделировании в качестве … берется модель той же физ. природы, что и исходный процесс. Разработка и реализация такой модели на практике трудновыполнима и требует больших физ. затрат. Второй подход основан на использовании мат. аппарата, который описывает физ. явления. При этом один и тот же мат. аппарат может описывать явления, физ. сущность которых различна. Такой подход получил название аналогового моделирования, а модель исх. процесса – аналоговой моделью. Осн. требованием к физ. модели явл-ся условие ее подобия исходному процессу. Подобие – это условие, при котором возможен количественный перенос рез-тов экспериментов с модели на оригинал. Применение методов теории подобия при физ. моделировании позволяет установить параметры модели, а также определить соотв. параметры моделир. процесса на основе данных полученных при измерениях на физ. модели. Подобие модели и оригинала дает возможность переноса рез-тов эксперимента с модели на оригинал с помощью критерия подобия. Физ. моделирование создает ряд. преимуществ в колич. исследовании сложных процессов. Физ. модель обычно выбирают на основе процессов для которых измерение параметров является технически более простым, чем для исх. исследуемого процесса. В то же время полученные результаты на выбранной физ. модели будут адекватны результатам, которые можно было бы получить при исследовании оригинала только если соблюдался принцип подобия модели и оригинала. Для сравнительно простых процессов принцип подобия оправдывает свое применение, т. к. в этом случае количество критериев подобия ограничено. Для анализа сложных процессов применение физ. моделирования затруднительно. Поэтому необх. использование мат. моделирования.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.244 (0.007 с.) |


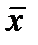
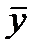 y
y
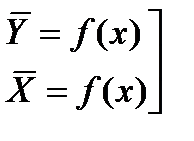 уравнения регрессии
уравнения регрессии

 , то функциональная связь прямая.
, то функциональная связь прямая.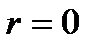 , то
, то 
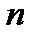 , при которых было произведении их вычисление.
, при которых было произведении их вычисление.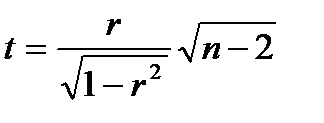 - Критерий Стьюдента
- Критерий Стьюдента , коэффициент правильный.
, коэффициент правильный.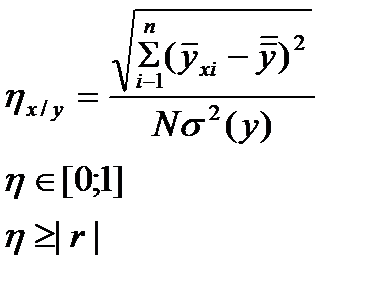
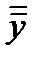 - среднее арифметическое
- среднее арифметическое - общее арифметическое
- общее арифметическое


