
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Роль моделирования в процессе научного исследованияСтр 1 из 8Следующая ⇒
Роль моделирования в процессе научного исследования Целью исследования является определение значений параметров исследуемого объекта, удовлетворяющих определенному критерию. Это означает, что в процессе исследования необходимо изменять значение параметров исследуемого объекта, и т. о. измерять значение показателя, служащего аргументом критерия. Процесс исследования заканчивается, когда исследователь находит совокупность значений параметров объекта, удовлетворяющую данному критерию с заданной достоверностью. Проведение таких исследований наз-ся экспериментом. Для проведения научных экспериментов реальные объекты заменяются соответствующими им более простыми безопасными и доступными объектами, свойства которых подобны св-вам исслед. реальных объектов в определенной существенной части. Объект, с целью изучения которого проводятся исследования наз-ся оригиналом, а объект, исследуемый вместо оригинала для изучения опред. св-в – моделью. Моделирование – это метод изучения св-в объектов оригиналов посредством исследования соотв. св-в их моделей. Мат. модель – образ исследуемого объекта, создаваемый с помощью определенных математических систем с целью изучения опред. св-в данного объекта. Для получения мат. модели необходимо: 1. Определить показатель данного свойства Со 2. Установить перечень св-в С1,…,СN, с которыми свойство Со связано некоторыми отношениями (внутренние свойства объекта и свойства внешней среды, влияющие на объект). 3. Описать в избранной форматной системе св-ва внешней среды, как внешние факторы Х1, Х2,…,Хn, влияющие на искомый показатель Y. Внутренние св-ва объекта – Z1,...,Zm Группа неучитываемых факторов – W1,...,Ws 4. Выяснить, если это возможно закономерное отношение между исследуемой величиной Y и всеми учитываемыми факторами и параметрами и составить мат. описание.
Y=f(X1,...,Xn; W1,...,Ws; Z1,...,Zm) В модели будут отображаться только те факторы реального объекта, которые имеют существенное значение для решения исследуемой модели. Кроме того измерение существенных факторов и параметров практически всегда содержит ошибки, вызываемые неточностью измерит. приборов и незнанием некоторых факторов. В силу этого, мат. модель является только приближенным описанием св-в изучаемого объекта. Подобие модели заключается в адекватности реакции Y/ и Y оригинала на изменение внешних факторов Х1,…, Хn, поэтому в общем случае мат. модель предст. собой ф-цию следующего вида.
Y/ = f(X1,...,Xn; P1,...,Pm) P1, Pm – внутр. параметры модели адекватные параметрам оригинала. В зависимости от применяемых методов мат. описания изучаемых объектов, мат. модели бывают аналитические, имитационные, логические, графические и т. д. Главным вопросом мат. моделирования явл-ся вопрос о том, как точно составленная мат. модель отражает отношение между учитываемыми факторами, параметрами и показателем Y, описываемого св-ва реального объект.
Основы методологии IDEF1 Предназначение стандарта IDEF1. Стандарт был разработан как инструмент для анализа и изучения взаимосвязей между инф. потоками в рамках коммерческой деятельности предприятия. Целью подобного исследования является дополнение и структуризация существующей информации и обеспечение качественного управления инф. потоками. Необходимость в подобной реорганизации инф. области возникает на начальном этапе построения инф. системы, и методология IDEF1 позволяет достаточно наглядно обнаружить «черные дыры» и слабые места в существующей структуре инф. потоков. Применение методологии IDEF1 как инструмента построения наглядной модели инф. структуры позволяет решить след. задачи 1. Выяснить структуру и содержание существующих потоков инф-ии на предприятии 2. Определить, какие проблемы, выявленные в рез-те функционального анализа и анализа потребности, вызванных недостатком управления соотв. инф-ей 3. Выявить инф. потоки, требующие доп. упр-я для эффект. реализации модели. С помощью IDEF1 происходит изучение сущ. информации о различных объектах в области деятельности предприятия. Характерно, что IDEF1 включает в рассмотрение не только автоматизированные компоненты, но и реальные объекты IDEF1 является аналитическим методом и исп-ся преимущественно для выполнения след. действий 1. Определение самой функции и структуры ее потоков, имеющей отношение к деятельности предприятия
2. Определение существующих правил и законов, по которым осущ-ся движение инф. потоков, а также принципов управления ими 3. Выяснение взаимосвязей между существующими инф. потоками в рамках предприятия 4. Выявление проблем, возникающих вследствие недостатка качественного управления Результаты анализа инф. потоков могут быть использованы для стратегического и тактического планирования деятельности предприятия и улучшения инф. управления. Наглядные IDEF-модели обеспечивают основу для построения мощной и гибкой инф. системы. Преимущества IDEF 1X. Основным преимуществом IDEF1X по сравнению с другими методами разраб. баз данных является жесткая и строгая стандартизация моделирования. Установленные стандарты позволяют избежать различ. трактовки построенной модели. Классификация моделей Физ. – воспроизведение постоянства определяющих критериев подобия. Физ. моделью некоторой системы наз-ют систему той же или иной природы, которая частично или полностью воспроизводить свойства исходной системы в рамках заданного приближения. Чаще всего в качестве модели исп-ся электрич. или электромагн. процессы. При этом исходные моделируемые процессы могут иметь разнообр. физ природу (мех., тепловую) Разновидностью физ. моделирования является исследование процесса той же физ. природы, но в другой области параметров (масштабные модели). Физ. моделир-е иногда является альтернативой мат. моделированию, но часто они дополняют друг друга. Мат. моделирование – качественное или количественное описание процесса с помощью мат. модели, при построении которой реальный процесс описывается с помощью того или иного мат. аппарата. Мат. модель сложного процесса, непосредственное проведение экспериментов на котором часто практически невозможно, позволяет исследовать его динамику, давая количественное описание процесса и устанавливает изменение количественного характера в динамике. Моделир. процессы разнообразные по своей природе и степени сложности. Все они делятся на детерминированные и стохастические. Детерминир-е – процессы, динамика которых полностью определяется начальными условиями и динамич. переменные являются функциями времени. Стохастические – процессы, параметры которых изменяются случайно под воздействием неконтролуируемых дестабилизирующих объектов. Поэтому однозначно предсказать поведение таких процессов на основе их изучения затруднительно. Поэтому, говорят лишь о их вероятности того или иного поведения. Мат. моделирование позволяет установить условия, при которых динамическая система переходит от детерминированного процесса к стохастическому. В соответствии с характером изучаемого процесса, строятся жесткие или вероятностные модели. Жесткие модели строятся без использования стахостич. вероятностных распределений. В этом случае определенному значению входного параметра будет соотв-ть опред. значение его выходного параметра. Связь между вх. и вых. параметрами явл-ся функциональной. Вероятностные модели описывают стох. процессы. Большинство совр. процессов носят случ. характер, когда вых. параметр связан с входным параметром статистически. В этом случае каждому определенному значению вх. параметра соотв. распределение значение вых. параметра. Поэтому вероятностные модели строятся с использованием методов теории вер-тей и мат. статистики.
17.Корреляционный анализ.Коэффициент корреляции. Корреляционное отношение Для построения матем. модели, отображаемой зависимость ф-ции оклика от фактора X Y=f(x) Стат.данные обрабатывают, подсчитывая среднее значение отклика Y для каждого определенного значения X
По виду графического изображения судят о наличии влияния одного параметра на другой.Если оно обнаружено, то говорят о наличии корреляционной связи между рассм. параметрами.
Цель корреляционного анализа – установление корреляционной связи между рассматриваемыми параметрами. Варианты: 1) X и Y связаны – зависимости обоими признаками могут выражаться в виде формулы. 2) X и Y не строго связаны – связь носит статический или вероятностный характер. 3) X и Y не связаны – связи нет.
Коэффициент корреляции:
Если Если При оценке коэффициента корреляции учитывается число пар наблюдений
Если В случае криволинейной связи между признаками оценка связи между ними осуществляется с помощью корреляционного отношения.
n – число наблюдений N – общее число наблюдений
σ – дисперсия Физическое моделирование Существует два подхода к физическому моделированию. В первом из них при изучении физики последовательно излагают физ. явления, основу которых составляют различные физ. процессы (мех., электромагнитные, ядерные и т. д.). В этом случае при физ. моделировании в качестве … берется модель той же физ. природы, что и исходный процесс. Разработка и реализация такой модели на практике трудновыполнима и требует больших физ. затрат. Второй подход основан на использовании мат. аппарата, который описывает физ. явления. При этом один и тот же мат. аппарат может описывать явления, физ. сущность которых различна. Такой подход получил название аналогового моделирования, а модель исх. процесса – аналоговой моделью. Осн. требованием к физ. модели явл-ся условие ее подобия исходному процессу. Подобие – это условие, при котором возможен количественный перенос рез-тов экспериментов с модели на оригинал.
Применение методов теории подобия при физ. моделировании позволяет установить параметры модели, а также определить соотв. параметры моделир. процесса на основе данных полученных при измерениях на физ. модели. Подобие модели и оригинала дает возможность переноса рез-тов эксперимента с модели на оригинал с помощью критерия подобия. Физ. моделирование создает ряд. преимуществ в колич. исследовании сложных процессов. Физ. модель обычно выбирают на основе процессов для которых измерение параметров является технически более простым, чем для исх. исследуемого процесса. В то же время полученные результаты на выбранной физ. модели будут адекватны результатам, которые можно было бы получить при исследовании оригинала только если соблюдался принцип подобия модели и оригинала. Для сравнительно простых процессов принцип подобия оправдывает свое применение, т. к. в этом случае количество критериев подобия ограничено. Для анализа сложных процессов применение физ. моделирования затруднительно. Поэтому необх. использование мат. моделирования. Регрессионный анализ Целью регрессионного анализа является установление формы связи между рассматриваемыми параметрами. Имеется n независимых переменных. При построении модели методом регрессионного анализа предполагается. 1. Рез-ты наблюдений Y1, Y2,..., Yn предст. собой независ. нормально распределенные случ. величины. 2. Дисперсии этих случ. величин σ2 равны друг другу, т. е. разброс рез-тов эксперимента в рассмотренной области постоянен. 3. Независ. переменные измеряются значительно точнее результир. функций σ2 (Х1)<< σ2 (Y) 4. Переменные Х1, Х2,..., Хk –линейно независимы. При сформулированных допущениях регрессионная модель получ-я методом наим. квадратов явл. оптимальной и позволяет извлечь из экспериментальных данных максимум информации. Задача построения модели идентификации сводится к определению коэф-тов из условия линеаризации суммы квадратов отклонений
Коэф. регрессии могут быть определены только совместно. Взаимосвязь коэф-тов исключает их физ. Интерпретацию. После вычисления коэффициентов регрессии необходимо провести статистич. анализ полученной модели. S2=S/fS - используется для определения адекватности модели Для оценки связи коэф-тов регрессии между собой используются методы корреляц. анализа, при этом строятся так называемая матрица ошибок, предст. собой ковариационную матрицу
Диагональные элементы матрицы опред. дисперсия коэф-тов регрессии, а недиаг. – взаимосвязь этих коэф-тов. Роль моделирования в процессе научного исследования Целью исследования является определение значений параметров исследуемого объекта, удовлетворяющих определенному критерию. Это означает, что в процессе исследования необходимо изменять значение параметров исследуемого объекта, и т. о. измерять значение показателя, служащего аргументом критерия.
Процесс исследования заканчивается, когда исследователь находит совокупность значений параметров объекта, удовлетворяющую данному критерию с заданной достоверностью. Проведение таких исследований наз-ся экспериментом. Для проведения научных экспериментов реальные объекты заменяются соответствующими им более простыми безопасными и доступными объектами, свойства которых подобны св-вам исслед. реальных объектов в определенной существенной части. Объект, с целью изучения которого проводятся исследования наз-ся оригиналом, а объект, исследуемый вместо оригинала для изучения опред. св-в – моделью. Моделирование – это метод изучения св-в объектов оригиналов посредством исследования соотв. св-в их моделей. Мат. модель – образ исследуемого объекта, создаваемый с помощью определенных математических систем с целью изучения опред. св-в данного объекта. Для получения мат. модели необходимо: 1. Определить показатель данного свойства Со 2. Установить перечень св-в С1,…,СN, с которыми свойство Со связано некоторыми отношениями (внутренние свойства объекта и свойства внешней среды, влияющие на объект). 3. Описать в избранной форматной системе св-ва внешней среды, как внешние факторы Х1, Х2,…,Хn, влияющие на искомый показатель Y. Внутренние св-ва объекта – Z1,...,Zm Группа неучитываемых факторов – W1,...,Ws 4. Выяснить, если это возможно закономерное отношение между исследуемой величиной Y и всеми учитываемыми факторами и параметрами и составить мат. описание.
Y=f(X1,...,Xn; W1,...,Ws; Z1,...,Zm) В модели будут отображаться только те факторы реального объекта, которые имеют существенное значение для решения исследуемой модели. Кроме того измерение существенных факторов и параметров практически всегда содержит ошибки, вызываемые неточностью измерит. приборов и незнанием некоторых факторов. В силу этого, мат. модель является только приближенным описанием св-в изучаемого объекта. Подобие модели заключается в адекватности реакции Y/ и Y оригинала на изменение внешних факторов Х1,…, Хn, поэтому в общем случае мат. модель предст. собой ф-цию следующего вида. Y/ = f(X1,...,Xn; P1,...,Pm) P1, Pm – внутр. параметры модели адекватные параметрам оригинала. В зависимости от применяемых методов мат. описания изучаемых объектов, мат. модели бывают аналитические, имитационные, логические, графические и т. д. Главным вопросом мат. моделирования явл-ся вопрос о том, как точно составленная мат. модель отражает отношение между учитываемыми факторами, параметрами и показателем Y, описываемого св-ва реального объект.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.187.103 (0.06 с.) |


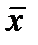
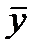 y
y
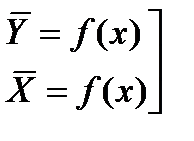 уравнения регрессии
уравнения регрессии

 , то функциональная связь прямая.
, то функциональная связь прямая.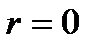 , то
, то 
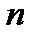 , при которых было произведении их вычисление.
, при которых было произведении их вычисление.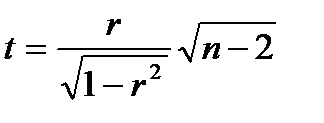 - Критерий Стьюдента
- Критерий Стьюдента , коэффициент правильный.
, коэффициент правильный.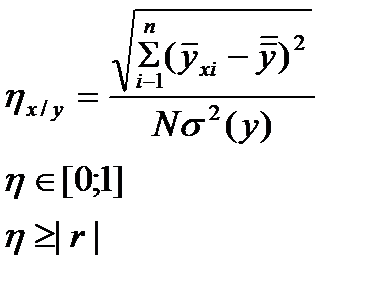
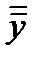 - среднее арифметическое
- среднее арифметическое - общее арифметическое
- общее арифметическое




