
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания по решению злп в среде ExсelСодержание книги
Поиск на нашем сайте ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Тверской государственный технический университет
Линейное программирование. Примеры решения задач в Excel. Тверь Методическое пособие предназначено для студентов специальности «Экономика и управление на предприятии (машиностроение)», изучающих курсы «Экономико-математические методы в управлении» и «Экономико-математические модели объектов отрасли». Пособие можно также рекомендовать студентам экономических специальностей, изучающих экономико-математические методы и модели. Обсуждено и рекомендовано на заседании кафедры ИПМ (протокол № от марта 2008 г.) Составители: Е.Е. Фомина, И.Л. Кислова
СОДЕРЖАНИЕ Введение. 4 1 Методические указания по решению ЗЛП в среде Exсel 7 1.1 Максимизация прибыли предприятия. 7 1.2 Максимизация годового дохода. 17 1.3 Специальные задачи линейного программирования. 25 1.3.1 Задача целочисленного программирования. 25 1.3.2 Транспортная задача. 26 1.3.2.1 Закрытая транспортная задача. 27 1.3.2.2 Открытая транспортная задача. 34 1.3.3 Задача о назначениях. 35 1.3.4 Двойственность в задачах линейного программирования...36 2. Вопросы для самоконтроля. 47 3. Варианты заданий. 48 4. Требования к оформлению контрольной работы.. 59 Использованная литература. 60
Введение В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции). Оптимизационные модели отражают в математической форме смысл экономической задачи. Отличительной особенностью этих моделей является наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяющих условиям задачи, и обеспечивают выбор оптимального решения, отвечающего критерию оптимальности.
Общая задача оптимизации В общем виде математическая постановка задачи математического программирования состоит в определении наибольшего или наименьшего значения целевой функции f (x1, x 2, …. x n) при условиях gi (x1 , x2,…, x n) ≤ bi; (i = 1,2, … m), где f и gi - заданные функции, а bi - некоторые действительные числа. Задачи математического программирования делятся на задачи линейного и нелинейного программирования. Если все функции f и gi - линейные, то соответствующая задачи является задачей линейного программирования (ЗЛП). Если хотя бы одна из указанные функций – нелинейная, то соответствующая задача является задачей нелинейного программирования. Линейное программирование – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т.е. линейных равенств или неравенств, связывающих эти переменные. К задачам линейного программирования сводится широкий круг вопросов планирования экономических процессов, где ставится задача поиска наилучшего (оптимального) решения. Cреди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования. Это задачи, в результате решения которых определяется минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве. В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования. В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения. Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно-линейного программирования. В общем виде задачи линейного программирования (ЗЛП) ставится следующим образом: Необходимо найти вектор
и удовлетворяющий условиям
где
Линейная функция f(X) называется целевой функцией задачи. Условия (2) называются функциональными, а (3) – прямыми ограничениями задачи. Вектор X=(x1, x2, … xn), компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП. Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений. Допустимое решение, максимизирующее целевую функцию f (X), называется оптимальным планом задачи. Будем считать, что ЗЛП записана в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные неотрицательные. На практике хорошо зарекомендовали себя следующие модели, относящиеся к оптимизационным: определения оптимальной производственной программы; оптимального смешивания компонентов; оптимального раскроя; оптимального размещения предприятий некоторой отрасли на определенной территории; формирования оптимального портфеля ценных бумаг; транспортной задачи. Для решения ЗЛП существует универсальный метод – метод последовательного улучшения плана, или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным базисом и симплекс-метода с искусственным базисом (М-метод). Выбор конкретной вычислительной процедуры осуществляется после приведения исходной задачи к каноническому виду задачи линейного программирования (КЗЛП):
В теории линейного программирования показано, что оптимальное решение ЗЛП связано с угловыми (крайними) точками многогранника решений, которым отвечают опорные планы (неотрицательные базисные решения системы уравнений КЗЛП). Каждый из опорных планов определяется системой m линейно независимых векторов, содержащихся в данной системе из n векторов А1,А2, …..Аn. Верхняя граница количества опорных планов, содержащихся в данной задаче, определяется числом сочетаний Cm. Решение ЗЛП симплекс-методом «вручную» подробно рассмотрено в [1], [5] и др. ЗЛП широко применяются в экономике и управлении. На практике хорошо зарекомендовали себя следующие модели, относящиеся к оптимизационным: · определения оптимальной производственной программы; · оптимального смешивания компонентов; · оптимального раскроя; · оптимального размещения предприятий некоторой отрасли на определенной территории; · формирования оптимального портфеля ценных бумаг; · транспортной задачи и др. Менеджер, как лицо ответственное за принятие решений, должен уметь использовать известные модели и понимать как полученный результат использовать для принятия разумного решения.
Огромный вклад в развитие и применение ЗЛП внес наш соотечественник Леонид Витальевич Канторович. За что в 1975 г. Был удостоен Нобелевской премии по экономике. Постановка задачи Для выпуска 4 - х видов продукции требуется сырье, рабочее время и оборудование. Для выпуска одной единицы продукции 1 - ого вида необходимо 3 ед. сырья, 22 ед. рабочего времени и 10 ед. оборудования. Для выпуска одной единицы продукции 2 - ого вида необходимо 5 ед. сырья, 14 ед. рабочего времени и 14 ед. оборудования. Для выпуска одной единицы продукции 3 - его вида необходимо 2 ед. сырья, 18 ед. рабочего времени и 8 ед. оборудования. Для выпуска одной единицы продукции 4 - ого вида необходимо 4 ед. сырья, 30 ед. рабочего времени и 16 ед. оборудования. Прибыль от продажи одной единицы продукции 1 - ого вида 30 руб., 2 - ого вида – 25 руб., 3 - его вида – 8 руб., 4 - ого вида – 16 руб. Ресурсы ограниченны: имеется 60 ед. сырья, 400 ед. рабочего времени и 120 ед. оборудования. А) Какое количество продукции каждого вида необходимо выпустить, чтобы максимизировать прибыль предприятия? Б) Все ли продукты вошли в оптимальный план или существуют убыточные? На сколько нужно увеличить прибыль от продажи одной единицы убыточной продукции, чтобы она вошла в оптимальный план? В) Каковы интервалы устойчивости для прибыли за одну единицу продукции каждого вида? Изменится ли оптимальное решение, если прибыли от продажи одной единицы продукции 4 – ого вида увеличить на 15 ед., 33 ед.? Уменьшить на 10 ед.? Г) Какие ресурсы являются дефицитными? Как изменится оптимальное решение, если ресурс оборудование увеличить на 1 ед., уменьшить на 100 ед., 50 ед.?
Для удобства сведем данные задачи в следующую таблицу: Таблица 1
Решение Целевая функция Т.к. цель задачи – максимизировать прибыль от продажи продукции (Р), то Р будет иметь вид: Р=30*x1+25*x2+8*x3+16* x4 (руб.) (*) Ограничения Исходя из выражения для целевой функции, можно увидеть, что чем больше будут значения x1, x2, x3,x4, тембольше будет прибыль Р. Однако беспредельно увеличивать выпуск продукции невозможно, т.к. ресурсы предприятия ограничены, что приводит к ограничениям на x1, x2, x3,x4. 3*x1+5*x2+2*x3+4*x4 22*x1+14*x2+18*x3+30*x4 10*x1+14*x2+8*x3+16*x4 xi Примечание: · В левой части i-ого i=1,2,3 функционального ограничения записано общее количество ресурса i-ого i=1,2,3 вида (сырья, рабочего времени и оборудования), необходимого для производства всей продукции. · В ограничениях фигурирует знак “ · Прямые ограничение (4) представляет собой следующее естественное условия: количество единиц выпускаемой продукции должно быть не отрицательным. Таблица 2
Ответ В результате решения задачи был получен следующий ответ: необходимо выпускать 12 ед. продукции первого вида, продукцию второго, третьего и четвертого вида выпускать не нужно При этом максимальная прибыль составит 360 руб.
Рис. 9 результат решения задачи Таблица 3 Раздел Изменяемые ячейки
Таблица 4 Раздел Ограничения
Примечание: Теневые цены и интервал устойчивости изменения запасов каждого из ресурсов, в котором значения теневых цен сохраняются, помогает менеджеру, не решая задачи заново, оценить, запасы какого ресурса нужно увеличить, чтобы максимально увеличить прибыль, и какого будет увеличение прибыли при заданном изменении данного запаса.
Постановка задачи Вкладчик располагает суммой в размере 50000 руб. Банки города предлагают следующие проценты по вкладам: 1 банк – 8,5% годовых, 2 банк – 7% годовых, 3 банк – 8% годовых. Вкладчик хочет распорядиться деньгами следующим образом: 1. Вся сумма должна быть вложена, 2. Не менее 55% суммы должно быть вложено во 2 банк, 3. В 3 банк должно быть вложено по крайней мере столько же, сколько и в 1 банк. А) Каким образом распределить деньги, чтобы получить максимальный годовой доход? Б) Каковы интервалы устойчивости процентных ставок банков? В) Как изменится годовой доход, если вкладчик внесет дополнительные средства? Решение Элементы модели Целевая функция Т.к. цель задачи – максимизировать общий годовой доход (D), то D будет иметь вид: D=x1*8,5%+x2*7%+x3*8% (руб.) (**) Ограничения Из предлагаемых процентных ставок банков видно, что чем больше денег будет вложено в 1 банк, тем больше будет годовой доход. Однако, вкладчик выдвигает ряд требований при вложении денег, что приводит к ограничениям на значения неизвестных x1, x2, x3. x1+x2+x3=50000, (5) x2 x1 xi Примечание: · В левой части ограничения (1) записана общая сумма денег, которую вкладчик хочет положить в банк под проценты, она должна быть равна 50000 руб. · В ограничении (2) фигурирует знак · Аналогично, в ограничении (3) стоит знак · Ограничение (4) представляет собой следующее естественное условие: количество денег, вкладываемое в каждый банк, должно быть не отрицательным. Таблица 5
Ответ В результате решения задачи был получен следующий ответ: В первый банк необходимо вложить 11250 руб., во второй банк – 27500 руб., в третий банк – 11250 руб. При этом максимальный годовой доход составит 3781,25 руб.
Рис. 19 результат решения задачи Анализ решения Используя данные отчета по устойчивости (см. рис. 20) проанализируем полученное решение.
Рис. 20 Отчет по устойчивости Таблица 6 Раздел Изменяемые ячейки
Таблица 7 Раздел Ограничения
Таблица 8
В данном случае, математическая модель аналогична математической модели Задачи 1, но добавляется новое условие xi – целые числа. Таблица 9
Данное условие оформляется в окне Поиск решения следующим образом (см. рис. 21):
Рис.21 Добавление ограничения Примечание: Для задач целочисленной оптимизации не предусмотрено вывода отчета по устойчивости.
Транспортная задача Постановка задачи Для строительства четырех объектов используется кирпич, изготавливаемый на трех заводах. Ежедневно каждый из заводов может изготавливать 100, 150 и 50 усл. ед. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов равны 70, 80, 60 и 90 усл. ед. Известны также тарифы перевозок 1 усл. ед. кирпича с каждого из заводов к каждому из строящихся объектов, они заданы матрицей С следующего вида:
Составить такой план перевозок кирпича от заводов к стоящимся объектам, при котором общая стоимость перевозок будет минимальной.
Представим данные задачи в виде следующей таблицы: Таблица 10
В данной задаче потребность всех объектов в кирпиче равна запасам всех заводов (70+80+60+90=100+150+50), т.е. она является закрытой, а следовательно разрешима. Решение Элементы модели Целевая функция S Цель задачи – минимизировать стоимость перевозок. Т.к. стоимость перевозки 1 усл. ед. от каждого завода к каждому объекту нам известна (см.*) т.о. S будет иметь вид: S=6*x11+7*x12+3*x13+5*x14+1*x21+2*x22+5*x23+6*x24+ +8*x31+10*x32+20*x33+1*x34 (руб.) Ограничения Так как возможности заводов по ежедневному производству кирпичей ограниченны, а строящиеся объекты имеют ежедневную потребность в кирпиче, то на неизвестные
Ограничения «на производство» кирпича: x11+x12+x13+x14=100, (13) x21+x22+x23+x24=150, (14) x31+x32+x33+x34=50, (15) Ограничения «на потребности» в кирпиче: x11+x21+x31=70, (16) x12+x22+x32=80, (17) x13+x23+x33=60, (18) x14+x24+x34=90, (19) xi xi – целые числа (21) Примечание: Ограничения (20) и (21) представляют собой следующие естественные условия: количество перевозимых кирпичей должно быть не отрицательным и целым.
Таблица 11
Ответ В результате решения задачи был получен следующий ответ: x11=0 (с первого завода на первый объект кирпичи не поставляются), x12=0 (с первого завода на второй объект кирпичи не поставляются), x13=60 (с первого завода на третий объект необходимо поставить 60 усл ед. кирпичей), … X34=50 (с третьего завода на четвертый объект необходимо поставить 50 усл. ед. кирпичей),
При этом минимальная стоимость перевозки будет 660 руб.,
Рис. 29 результат решения задачи Постановка задачи Изменим условие задачи 4 следующим образом: допустим, что потребность первого завода в кирпиче возросла вдвое и составила 140 ед. кирпича в день. Остальные данные остались неизменными. Таблица 12
Данная задаче уже является открытой, т.к. 140+80+60+9>100+150+50, т.е. потребности превышают запасы на 160 ед. Введем нового поставщика - IV завод с возможностью 160 ед. Так как груз от фиктивного поставщика к фиктивному потребителю не перевозится, то стоимость перевозок полагается равной нулю. Таблица 12 примет вид: Таблица 13
Данная задача уже является закрытой и решается аналогично задаче
Задача о назначениях Постановка задачи Мастер должен расставить трех рабочих для выполнения трех операций. Причем, каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим. Известно сколько минут в среднем тратит каждый из рабочих на выполнение каждой операции. Данные представлены в таблице:
Как распределить рабочих по операциям, чтобы минимизировать суммарные затраты рабочего времени? Решение Элементы модели Целевая функция V Цель задачи – минимизировать суммарные затраты рабочего времени. Т.к. время выполнения каждым рабочим каждой операции известно, то можно составить целевую функцию. V будет иметь вид: V=10*x11+12*x12+14*x13+ +11*x21+13*x22+14*x23+ +10*x31+9*x32+12*x33 ( мин .) Ограничения Так каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим, то на неизвестные
Каждый рабочий выполняет только одну операцию x11+x12+x13=1, (22) x21+x22+x23=1, (23) x31+x32+x33=1, (24) Каждая операция выполняется только одни рабочим x11+x21+x31=1, (25) x12+x22+x32=1, (26) x13+x23+x33=1, (27) xi –двоичные (28) Примечание: Ограничение 7 представляют собой следующие условие:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.149 (0.009 с.) |

 , максимизирующий линейную форму
, максимизирующий линейную форму (1)
(1) (2)
(2) , (3)
, (3) ,
,  ,
,  - действительные числа.
- действительные числа.


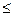 60, (1)
60, (1) 0, i=1,2,3,4, (4)
0, i=1,2,3,4, (4)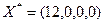 .
. .
.
 = (0, 8,57, 0, 0),
= (0, 8,57, 0, 0),
 =360 руб.
Аналогичные расчеты можно проделать для 3 – его и 4 – ого продукта.
=360 руб.
Аналогичные расчеты можно проделать для 3 – его и 4 – ого продукта.
 +
+  где
где  - теневая цена.
Теневая цена, также определяет ценность ресурса для производителя, если она отлична от 0, то ресурс считается дефицитным.
- теневая цена.
Теневая цена, также определяет ценность ресурса для производителя, если она отлична от 0, то ресурс считается дефицитным.
 =3.
Также, исходя из ограничения (3), видно, что оборудование использовано на 100 % (левая часть ограничения равна правой), в то время как остальные ресурсы использованы не полностью (левая часть ограничения меньше правой).
Пример:
Если дефицитный ресурс оборудование увеличить на 1 ед., то оптимальная прибыль изменится и станет равной
=3.
Также, исходя из ограничения (3), видно, что оборудование использовано на 100 % (левая часть ограничения равна правой), в то время как остальные ресурсы использованы не полностью (левая часть ограничения меньше правой).
Пример:
Если дефицитный ресурс оборудование увеличить на 1 ед., то оптимальная прибыль изменится и станет равной  ,
где
,
где  -величина увеличении ресурса,
-величина увеличении ресурса,  = 50 ед., то оптимальная прибыль составит
= 50 ед., то оптимальная прибыль составит  =360+50*3=510 руб.
=360+50*3=510 руб.
 =360-50*3=60 руб.
=360-50*3=60 руб.


 = 3893,75 руб.
= 3893,75 руб.
 +
+  = 3781,25+0,075625=
3893,8279 руб.
= 3781,25+0,075625=
3893,8279 руб.
 = 10000 руб., то годовой доход изменится следующим образом:
D=
= 10000 руб., то годовой доход изменится следующим образом:
D=  = 3781,25+10000*0,075625=4537,5 руб.
= 3781,25+10000*0,075625=4537,5 руб.
 = 3781,25-10000*0,075625=3025 руб.
= 3781,25-10000*0,075625=3025 руб.

 . (***)
. (***) Объекты
Заводы
Объекты
Заводы
 накладывается ряд ограничений:
накладывается ряд ограничений: .
. .
.
 Объекты
Заводы
Объекты
Заводы
 Объекты
Заводы
Объекты
Заводы

 i =1,2,3, j = 1,2,3,.
i =1,2,3, j = 1,2,3,.



