
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел III функции нескольких переменныхСодержание книги
Поиск на нашем сайте
Тема 5 Функции нескольких переменных
Функции двух и нескольких переменных. Частные производные и техника дифференцирования. Экстремум функции двух переменных и его необходимое условие. Понятие об эмпирических формулах и методе наименьших квадратов. Построение методом наименьших квадратов линейной функции по эмпирическим данным (вывод системы нормальных уравнений). (1, гл. 15, § 15.1, 15.3, 15.6, 15.8; с. 397–400, 404–406, 410–413); (2, гл. 15). При изучении этой темы необходимо проводить сравнение с функциями одной переменной и по аналогии определять область определения, но только множеством точек плоскости, а также графики в виде поверхности в пространстве (1, пример 15.2, с.400). При определении частной производной необходимо использовать понятие частного приращения. Техника дифференцирования функции двух переменных включает те же правила и принципы, которые использовались для нахождения производных функций одной переменной (1, пример 15.7, 15.8, с.405–406). Метод наименьших квадратов имеет большое прикладное значение в экономических исследованиях. Эмпирическая формула включает неизвестные переменные, а критерием ее точности является функция этих параметров, то есть функция нескольких переменных. Критерий минимизируют, то есть находят экстремум функции нескольких переменных, получают с помощью метода наименьших квадратов формулу, которая является приближением с заданной точностью таблично заданной функции (1, пример 15.11), (2, с.363 –368). Необходимо обратить внимание на оценку погрешности приближения. Разобрать задачи с решениями (1, N15.7, 15.9, 15.13), для самостоятельного решения (1, N 15.23–15.32, 15.39). Раздел IV Дифференциальные уравнения
Тема 6 Дифференциальные уравнения
Понятие о дифференциальных уравнениях. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса. Дифференциальные уравнения первого порядка (неполные, с разделяющимися переменными, однородные и линейные). (1, гл. 12, § 12.1, 12.4–12.7, с. 325–328; 334–340); (2, гл. 2). Студентам необходимо усвоить определение дифференциального уравнения – как уравнения, которое связывает искомую функцию одной или нескольких переменных и производные различных порядков данной функции. Дифференциальные уравнения от одной переменной называется обыкновенным дифференциальным уравнением, в дифференциальные уравнения от нескольких переменных – дифференциальные уравнения в частных производных. Порядок дифференциального уравнения равен порядку старшей степени производной xy¢¢¢-xy¢+5=0 – уравнение третьего порядка. Нужно помнить, что задача интегрирования дифференциального уравнения – это задача нахождения искомого решения, а график решения называется интегральной кривой. Общее решение дифференциального уравнения – это решение, которое является функцией переменных х и n произвольных независимых постоянных С1, С2, С0…,Сn. Частное решение дифференциального уравнения – это решение, полученное из общего при некоторых значениях постоянных. Для ряда типов дифференциальных уравнений нужно знать студенту основные понятия, нужно уметь решать однородные дифференциальные уравнения, линейные дифференциальные уравнения, неполные дифференциальные уравнения и дифференциальные уравнения с разделяющимися переменными. Разобрать задачи (1, 12.8–12.22, 12.31–12.32, 12.45–12.47, 12.65). Решить самостоятельно (2, 12.17–12.30, 12.48–12.57, 12.62–12.69, 12.78). Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий
ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ ВАРИАНТ №1
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы:
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение: х2dу = у2dх, если при х = 1; у = 1.
ВАРИАНТ №2 Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1. Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №3 Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №4
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №5
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №6
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №7
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №8
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №9
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №10
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
Основная литература: 1. Абрамов, А.А. Введение в тензорный анализ и риманову геометрию: учеб. пособие для вузов / А.А.Абрамов. - 2-е изд. - М.: Физматлит, 2004. - 111с. 2. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. - М.: Логос, 2004. - 184 с. + 1 эл. опт. диск (CD-ROM). 3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006. - 432 с. 4. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2005. - 432 с. 5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. - 4-е изд., стереотип. - М.: Дрофа, 2004. - 725 с. 6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. - 3-е изд., испр. - М.: ДРОФА, 2001. - 725 с. 7. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий. - 3-е изд., испр. - М.: ДРОФА, 2001. - 712 с. 8. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. - СПб.: Питер, 2004. - 538с. 9. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. - М.: Физматлит, 2002. - 351 с. 10. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2006. 11. Мартинсон, Л.К. Дифференциальные уравнения математической физики: учеб. для втузов / Л.К.Мартинсон, Ю.И.Малов; Ред. В.С. Зарубин, А.П.Крищенко. - 2-е изд. - М.: МГТУ им. Н.Э. Баумана, 2002. - 367 с. 12. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов. - 5-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 479 с. 13. Пантелеев, А.В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах: учеб. пособие для втузов / А.В.Пантелеев, Якимова А.С. - М.: Высш. шк., 2001. - 446 с. 14. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. для втузов. В 2 т. Т. 1 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 415 с. 15. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учебник для втузов. В 2 т. Т. 2 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 544 с. 16. Полянин, А.Д. Методы решения нелинейных уравнений математической физики и механики: учеб. пособие для вузов / А.Д.Полянин, В.Ф.Зайцев, А.И.Журов. - М.: Физматлит, 2005. - 254 с. 17. Русак, В.Н. Математическая физика: учеб. пособие для ун-тов / В.Н.Русак. - 2-е изд., испр. - М.: Едиториал УРСС, 2006. - 244 с. 18. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления: учеб. для вузов. В 3 т. Т. 3 / Г.М. Фихтенгольц. - 8-е изд. - М.: ФИЗМАТЛИТ, 2003. - 727 с. 19. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 1 / Г.М. Фихтенгольц. - 6-е изд., стер. - СПб. Лань, 2005. - 440 с. - Алф. указ.: С. 434-440. 20. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 2 / Г.М.Фихтенгольц. - 6-е изд., стер. - СПб.: Лань, 2005. - 463 с. 21. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 1 / Г. М. Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 440 с. 22. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 2 / Г. М.Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 463 с. 23. Шипачев, В.С. Математический анализ: учеб. пособие для вузов / В.С.Шипачев. - М.: Высш. шк., 2002. - 176 с.
Дополнительная литература: 1. Антоневич, А.Б. Задачи и упражнения по функциональному анализу. Учеб.пособие. / А.Б.Антоневич, П.Н.Князев, Я.В.Радыно – М.: Едиториал УРСС, 2004 – 205с. 2. Босс, В. Лекции по математике: анализ. / В.Босс – М.: Едиториал УРСС, 2004 – 213с. 3. Босс, В. Лекции по математике: дифференциальные уравнения. / В.Босс– М.: Едиториал УРСС, 2004 – 204 с. 4. Васильева, А.Б. Интегральные уравнения / А.Б.Васильева, Н.А.Тихонов. - 2-е изд. - М.: ФИЗМАТЛИТ, 2004. – 175с. 5. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко [и др.]. - 7-е изд., испр. - М.: Оникс: Мир и Образование(М.), 2008. - 448 с. 6. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, С.П.Данко. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2007. - 416 с. 7. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2005. - 416 с. 8. Ерофеенко, В.Т. Уравнения с частными производными и математические модели в экономике: курс лекций / В.Т.Ерофеенко, И.С.Козловская. - 2-е изд., перераб. и доп. - М.: Едиториал УРСС, 2004. - 244с. 9. Задачи и упражнения по математическому анализу для втузов / Ред. Б.П.Демидович. – М.: АСТ-Астрель, 2004. - 495 с. 10. Зайцев, В.Ф. Справочник по обыкновенным дифференциальным уравнениям / В.Ф.Зайцев, А.Д.Полянин. - М.: Физматлит, 2001. - 576 с. 11. Краснов, М.Л. Операционное исчисление. Теория устойчивости: Задачи и примеры с подробными решениями: учеб.пособие. / М.Л.Краснов, А.И.Киселев, Г.И. Крамаренко – М.: Едиториал УРСС, 2003 – 175с. 12. Краснов, М.Л., Интегральные уравнения. Задачи и примеры с подробными решениями: учеб.пособие. / М.Л.Краснов, А.И.Киселев, Г.И. Крамаренко – М.: Едиториал УРСС, 2003 – 192с. 13. Кудрявцев, Л.Д. Краткий курс математического анализа: учеб. для вузов. В 2 т. Т. 1 Дифференциальное и интегральное исчисления функции одной переменной. Ряды / Л.Д.Кудрявцев. - 2-е изд., перераб. и доп. - Висагинас: Alfa, 1998. - 397 с. 14. Лукьянов, А.В. Введение в теорию уравнений с частными производными и математическую физику: метод. указания по решению уравнений теплопроводности / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2006. - 59 с. 15. Математический анализ и линейная алгебра. Учебное–методическое пособие. / Под ред. Н.Ш.Кремера. – М.: ВЗФЭИ, 2002. 16. Подчуфаров, Ю.Б. Физико-математическое моделирование систем управления и комплексов / Ю.Б.Подчуфаров; Ред. А.Г. Шипунов. - М.: Физматлит, 2002. - 167 с. 17. Привалов, И.И. Введение в теорию функций комплексного переменного: учеб. для вузов / И.И. Привалов - 14-е изд., стереотип. - М.: Высш. шк., 1999. - 432с. 18. Сборник задач и упражнений по математическому анализу. Ч.1 / С.И.Ляшко [и др.]; Ред. И.И. Ляшко. - М.; СПб.; Киев: Диалектика, 2001. - 430 с. 19. Сикорский, Ю.С. Обыкновенные дифференциальные уравнения. С приложением их к некоторым техническим задачам / Ю.С.Сикорский; Ред. С.Г. Михлин. - 2-е изд., стереотип. - М.: УРСС, 2005. - 155 с. 20. Стакун, А.А. Математический анализ: конспект лекций с решениями типовых примеров и метод. указ. к инд. заданиям (для студ.-заоч.). В 2 ч. Ч.2 / А.А.Стакун, С.И.Фролов. - СПб.: Политехника, 2001. - 147 с. 21. Цлаф, Л.Я. Вариационное исчисление и интегральные уравнения: справ. рук. / Л.Я.Цлаф. - 3-е изд., стереотип. – М.: Лань, 2005. - 191 с.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.110.150 (0.008 с.) |





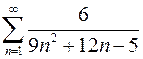
 2.
2. 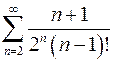

 2.
2. 


 2.
2. 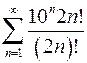


 2.
2. 


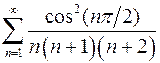 2.
2. 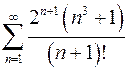


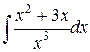 2.
2. 


 2.
2. 


 2.
2. 


 2.
2. 


 2.
2. 

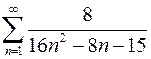
 2.
2. 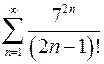


 2.
2. 
 Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 3. Исследовать несобственный интеграл на сходимость
 2.
2. 
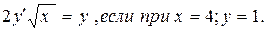

 2.
2. 


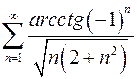 2.
2. 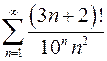


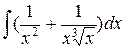 2.
2. 


 2.
2. 


 2.
2. 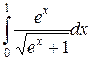

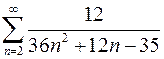
 2.
2. 




