
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1 Неопределенный интегралСодержание книги
Поиск на нашем сайте
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ.. 15 РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ.. 22
ВВЕДЕНИЕ Цель курса математический анализ в системе подготовки – освоение необходимого математического аппарата. Задачи изучения математического анализа как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке навыков решения основных задач математического анализа, что в конечном итоге формирует навык исследования моделей реальных процессов. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ Раздел IИНТЕГРАЛЬНОЕ ИCЧИЛЕНИЕ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Тема 1 Неопределенный интеграл
Понятие первообразной и неопределенного интеграла. Свойства неопределенного интеграла (с доказательством). Таблица основных интегралов. Интегрирование методом разложения, замены переменной и по частям. Понятие о «неберущихся» интегралах. (1, гл. 10, § 10.1–10.5, 10.8; с. 247–265); (2, гл. 10); (3,гл.9). Студенту необходимо, прежде всего, разобраться в принципиальном вопросе: интегральное исчисление решает обратную задачу – нахождение самой функции по ее производной. Эта задача является более сложной по сравнению с задачей дифференцирования. Понятие первообразной функции (1, с.251) связывается геометрической интерпретацией, когда первообразные отличаются на число (константу). Отсюда следует определение неопределенного интеграла, как «совокупность всех первообразных для функции f(x) на промежутке Х (ось абсцисс)». òf(x)dx=F(x)+C, f(x) – подинтегральная функция, f(x)dx – подынтегральное выражение, F(x) – первообразная функция, ò – знак интеграла, С – константа. Следует изучить свойства (с доказательствами) неопределенного интеграла (1, с.253, 254), знать табличные интегралы (1, с.255). Обратить внимание на свойство 2 (1, с.253): дифференциал неопределенного интеграла равен подынтегральному выражению d(òf(x)dx)=f(x)dx, то есть операции интегрирования и дифференцирования взаимно обратны (знаки d и ò взаимно уничтожают друг друга). Непосредственное интегрирование предполагает (1, примеры 1.10–10.3, с.255–257) сведение интегралов к табличным за счет тождественных преобразований и основных правил интегрирования. Для вычисления интегралов применяют линейную подстановку t=kx+b, а также другие подстановки: а) переменная интегрирования х заменяется функцией переменной t: x=j(t), а dx=j¢(t)dt; òf(x)dx=òf(j(t))j¢(t)dt; б) новая переменная t вводится как функция переменной интегрирования x: t=j(x), dt=j¢(x)dx; òf(j(x))j¢(x)dx=òf(t)dt. Последнюю подстановку удобно применять, если подынтегральное выражение содержит дифференциал (производную) функции j(х) с точностью до постоянного множителя. Если интеграл, полученный после замены переменной, стал «проще» данного (преобразован в табличный или приводящийся к табличному), то цель подстановки достигнута. После интегрирования функции по переменной t необходимо вернуться к прежней переменной х, выразив t через хпо формуле, применявшейся при подстановке. Примеры различных подстановок даны в (1, § 10.3, 10.6). Практическое применение формулы интегрирования по частям ((10.21), с. 263), если оно целесообразно, связано с проблемой правильного разбиения подынтегральноговыражения на сомножители u и dv. Отметим, что формулу интегрирования по частям, как правило, удобно применять, если подынтегральная функция является произведением многочлена на показательную или логарифмическую функцию (1, примеры 10.10–10.13, с. 263-269). Рекомендуется разобрать задачи с решениями N 10.1–10.4, 10.6–10.8, 10.9-10.11, 10.13, 10.14, 10.18а, 10.23, 10.24а, 10.25-10.27 и задачи для самостоятельного решения N 10.33-10.39, 10.41-10 45, 10 47–10.54, 10.55–10.59, 10.61, 10.63-10.65, 10.68–10.70 по учебнику (1) и аналогичные задачи по практикуму (2), обратив особое внимание на интегрирование методом подстановки.
Раздел II Ряды Тема 4 Числовые ряды
ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ ВАРИАНТ №1
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы:
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение: х2dу = у2dх, если при х = 1; у = 1.
ВАРИАНТ №2 Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1. Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №3 Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №4
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №5
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №6
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №7
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №8
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №9
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
ВАРИАНТ №10
Задание № 1. Найти точки экстремума функции нескольких переменных:
Задание № 2. Найти интегралы: 1.
Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 4. Вычислить сумму ряда Задание № 5. Исследовать ряды на сходимость 1. Задание № 6. Решить дифференциальное уравнение:
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
Основная литература: 1. Абрамов, А.А. Введение в тензорный анализ и риманову геометрию: учеб. пособие для вузов / А.А.Абрамов. - 2-е изд. - М.: Физматлит, 2004. - 111с. 2. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. - М.: Логос, 2004. - 184 с. + 1 эл. опт. диск (CD-ROM). 3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006. - 432 с. 4. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2005. - 432 с. 5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. - 4-е изд., стереотип. - М.: Дрофа, 2004. - 725 с. 6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. - 3-е изд., испр. - М.: ДРОФА, 2001. - 725 с. 7. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий. - 3-е изд., испр. - М.: ДРОФА, 2001. - 712 с. 8. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. - СПб.: Питер, 2004. - 538с. 9. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. - М.: Физматлит, 2002. - 351 с. 10. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2006. 11. Мартинсон, Л.К. Дифференциальные уравнения математической физики: учеб. для втузов / Л.К.Мартинсон, Ю.И.Малов; Ред. В.С. Зарубин, А.П.Крищенко. - 2-е изд. - М.: МГТУ им. Н.Э. Баумана, 2002. - 367 с. 12. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов. - 5-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 479 с. 13. Пантелеев, А.В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах: учеб. пособие для втузов / А.В.Пантелеев, Якимова А.С. - М.: Высш. шк., 2001. - 446 с. 14. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. для втузов. В 2 т. Т. 1 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 415 с. 15. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учебник для втузов. В 2 т. Т. 2 / Н.С.Пискунов. - Стер. изд. - М.: ИНТЕГРАЛ-ПРЕСС, 2004. - 544 с. 16. Полянин, А.Д. Методы решения нелинейных уравнений математической физики и механики: учеб. пособие для вузов / А.Д.Полянин, В.Ф.Зайцев, А.И.Журов. - М.: Физматлит, 2005. - 254 с. 17. Русак, В.Н. Математическая физика: учеб. пособие для ун-тов / В.Н.Русак. - 2-е изд., испр. - М.: Едиториал УРСС, 2006. - 244 с. 18. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления: учеб. для вузов. В 3 т. Т. 3 / Г.М. Фихтенгольц. - 8-е изд. - М.: ФИЗМАТЛИТ, 2003. - 727 с. 19. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 1 / Г.М. Фихтенгольц. - 6-е изд., стер. - СПб. Лань, 2005. - 440 с. - Алф. указ.: С. 434-440. 20. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 2 / Г.М.Фихтенгольц. - 6-е изд., стер. - СПб.: Лань, 2005. - 463 с. 21. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 1 / Г. М. Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 440 с. 22. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 2 / Г. М.Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 463 с. 23. Шипачев, В.С. Математический анализ: учеб. пособие для вузов / В.С.Шипачев. - М.: Высш. шк., 2002. - 176 с.
Дополнительная литература: 1. Антоневич, А.Б. Задачи и упражнения по функциональному анализу. Учеб.пособие. / А.Б.Антоневич, П.Н.Князев, Я.В.Радыно – М.: Едиториал УРСС, 2004 – 205с. 2. Босс, В. Лекции по математике: анализ. / В.Босс – М.: Едиториал УРСС, 2004 – 213с. 3. Босс, В. Лекции по математике: дифференциальные уравнения. / В.Босс– М.: Едиториал УРСС, 2004 – 204 с. 4. Васильева, А.Б. Интегральные уравнения / А.Б.Васильева, Н.А.Тихонов. - 2-е изд. - М.: ФИЗМАТЛИТ, 2004. – 175с. 5. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко [и др.]. - 7-е изд., испр. - М.: Оникс: Мир и Образование(М.), 2008. - 448 с. 6. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, С.П.Данко. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2007. - 416 с. 7. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. - 6-е изд. - М.: Оникс: Мир и Образование(М.), 2005. - 416 с. 8. Ерофеенко, В.Т. Уравнения с частными производными и математические модели в экономике: курс лекций / В.Т.Ерофеенко, И.С.Козловская. - 2-е изд., перераб. и доп. - М.: Едиториал УРСС, 2004. - 244с. 9. Задачи и упражнения по математическому анализу для втузов / Ред. Б.П.Демидович. – М.: АСТ-Астрель, 2004. - 495 с. 10. Зайцев, В.Ф. Справочник по обыкновенным дифференциальным уравнениям / В.Ф.Зайцев, А.Д.Полянин. - М.: Физматлит, 2001. - 576 с. 11. Краснов, М.Л. Операционное исчисление. Теория устойчивости: Задачи и примеры с подробными решениями: учеб.пособие. / М.Л.Краснов, А.И.Киселев, Г.И. Крамаренко – М.: Едиториал УРСС, 2003 – 175с. 12. Краснов, М.Л., Интегральные уравнения. Задачи и примеры с подробными решениями: учеб.пособие. / М.Л.Краснов, А.И.Киселев, Г.И. Крамаренко – М.: Едиториал УРСС, 2003 – 192с. 13. Кудрявцев, Л.Д. Краткий курс математического анализа: учеб. для вузов. В 2 т. Т. 1 Дифференциальное и интегральное исчисления функции одной переменной. Ряды / Л.Д.Кудрявцев. - 2-е изд., перераб. и доп. - Висагинас: Alfa, 1998. - 397 с. 14. Лукьянов, А.В. Введение в теорию уравнений с частными производными и математическую физику: метод. указания по решению уравнений теплопроводности / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2006. - 59 с. 15. Математический анализ и линейная алгебра. Учебное–методическое пособие. / Под ред. Н.Ш.Кремера. – М.: ВЗФЭИ, 2002. 16. Подчуфаров, Ю.Б. Физико-математическое моделирование систем управления и комплексов / Ю.Б.Подчуфаров; Ред. А.Г. Шипунов. - М.: Физматлит, 2002. - 167 с. 17. Привалов, И.И. Введение в теорию функций комплексного переменного: учеб. для вузов / И.И. Привалов - 14-е изд., стереотип. - М.: Высш. шк., 1999. - 432с. 18. Сборник задач и упражнений по математическому анализу. Ч.1 / С.И.Ляшко [и др.]; Ред. И.И. Ляшко. - М.; СПб.; Киев: Диалектика, 2001. - 430 с. 19. Сикорский, Ю.С. Обыкновенные дифференциальные уравнения. С приложением их к некоторым техническим задачам / Ю.С.Сикорский; Ред. С.Г. Михлин. - 2-е изд., стереотип. - М.: УРСС, 2005. - 155 с. 20. Стакун, А.А. Математический анализ: конспект лекций с решениями типовых примеров и метод. указ. к инд. заданиям (для студ.-заоч.). В 2 ч. Ч.2 / А.А.Стакун, С.И.Фролов. - СПб.: Политехника, 2001. - 147 с. 21. Цлаф, Л.Я. Вариационное исчисление и интегральные уравнения: справ. рук. / Л.Я.Цлаф. - 3-е изд., стереотип. – М.: Лань, 2005. - 191 с. СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ.. 15 РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ.. 22
ВВЕДЕНИЕ Цель курса математический анализ в системе подготовки – освоение необходимого математического аппарата. Задачи изучения математического анализа как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке навыков решения основных задач математического анализа, что в конечном итоге формирует навык исследования моделей реальных процессов. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ Раздел IИНТЕГРАЛЬНОЕ ИCЧИЛЕНИЕ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Тема 1 Неопределенный интеграл
Понятие первообразной и неопределенного интеграла. Свойства неопределенного интеграла (с доказательством). Таблица основных интегралов. Интегрирование методом разложения, замены переменной и по частям. Понятие о «неберущихся» интегралах. (1, гл. 10, § 10.1–10.5, 10.8; с. 247–265); (2, гл. 10); (3,гл.9). Студенту необходимо, прежде всего, разобраться в принципиальном вопросе: интегральное исчисление решает обратную задачу – нахождение самой функции по ее производной. Эта задача является более сложной по сравнению с задачей дифференцирования. Понятие первообразной функции (1, с.251) связывается геометрической интерпретацией, когда первообразные отличаются на число (константу). Отсюда следует определение неопределенного интеграла, как «совокупность всех первообразных для функции f(x) на промежутке Х (ось абсцисс)». òf(x)dx=F(x)+C, f(x) – подинтегральная функция, f(x)dx – подынтегральное выражение, F(x) – первообразная функция, ò – знак интеграла, С – константа. Следует изучить свойства (с доказательствами) неопределенного интеграла (1, с.253, 254), знать табличные интегралы (1, с.255). Обратить внимание на свойство 2 (1, с.253): дифференциал неопределенного интеграла равен подынтегральному выражению d(òf(x)dx)=f(x)dx, то есть операции интегрирования и дифференцирования взаимно обратны (знаки d и ò взаимно уничтожают друг друга). Непосредственное интегрирование предполагает (1, примеры 1.10–10.3, с.255–257) сведение интегралов к табличным за счет тождественных преобразований и основных правил интегрирования. Для вычисления интегралов применяют линейную подстановку t=kx+b, а также другие подстановки: а) переменная интегрирования х заменяется функцией переменной t: x=j(t), а dx=j¢(t)dt; òf(x)dx=òf(j(t))j¢(t)dt; б) новая переменная t вводится как функция переменной интегрирования x: t=j(x), dt=j¢(x)dx; òf(j(x))j¢(x)dx=òf(t)dt. Последнюю подстановку удобно применять, если подынтегральное выражение содержит дифференциал (производную) функции j(х) с точностью до постоянного множителя. Если интеграл, полученный после замены переменной, стал «проще» данного (преобразован в табличный или приводящийся к табличному), то цель подстановки достигнута. После интегрирования функции по переменной t необходимо вернуться к прежней переменной х, выразив t через хпо формуле, применявшейся при подстановке. Примеры различных подстановок даны в (1, § 10.3, 10.6). Практическое применение формулы интегрирования по частям ((10.21), с. 263), если оно целесообразно, связано с проблемой правильного разбиения подынтегральноговыражения на сомножители u и dv. Отметим, что формулу интегрирования по частям, как правило, удобно применять, если подынтегральная функция является произведением многочлена на показательную или логарифмическую функцию (1, примеры 10.10–10.13, с. 263-269). Рекомендуется разобрать задачи с решениями N 10.1–10.4, 10.6–10.8, 10.9-10.11, 10.13, 10.14, 10.18а, 10.23, 10.24а, 10.25-10.27 и задачи для самостоятельного решения N 10.33-10.39, 10.41-10 45, 10 47–10.54, 10.55–10.59, 10.61, 10.63-10.65, 10.68–10.70 по учебнику (1) и аналогичные задачи по практикуму (2), обратив особое внимание на интегрирование методом подстановки.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.134.18 (0.008 с.) |









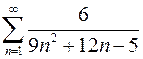
 2.
2. 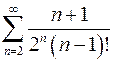

 2.
2. 


 2.
2. 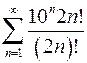


 2.
2. 


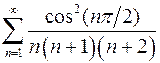 2.
2. 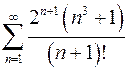


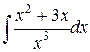 2.
2. 


 2.
2. 


 2.
2. 


 2.
2. 


 2.
2. 

 2.
2. 


 2.
2. 
 Задание № 3. Исследовать несобственный интеграл на сходимость
Задание № 3. Исследовать несобственный интеграл на сходимость
 2.
2. 
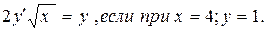

 2.
2. 


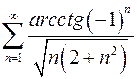 2.
2. 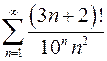


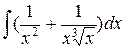 2.
2. 


 2.
2. 


 2.
2. 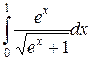

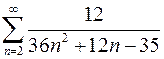
 2.
2. 




