
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородные линейные дифференциальные уравнения (ОЛДУ)Содержание книги
Поиск на нашем сайте
Рассмотрим следующие свойства однородного ЛДУ
1) Если 2) Если 3) Если функции
также является решением этого уравнения. 3.3. Линейная независимость функций Определение. Функции
выполняется только при всех Функциональный определитель вида
называется определителем Вронского (вронскианом) n- го порядка для системы функций Теорема (необходимое и достаточное условие линейной независимости решений). Для того чтобы частные решения однородного ЛДУ (3.1)
3.4. Общее решение линейного однородного дифференциального уравнения n -го порядка Рассмотрим однородное линейное дифференциальное уравнение
Если n частных решений Теорема. Если
является общим решением этого линейного дифференциального уравнения. Понятие комплексного числа Мнимой единицей называется такое число Определение.Комплексным числом называется число вида
где Запись числа в виде (3.7) называется алгебраической формой записи комплексного числа Если Плоскость, на которой выбрана декартова система координат с осями  называется действительной(или вещественной) осью, на ней изображаются действительные числа. Ось называется действительной(или вещественной) осью, на ней изображаются действительные числа. Ось  называется мнимой осью, на ней изображаются мнимые числа вида называется мнимой осью, на ней изображаются мнимые числа вида  . Число . Число  изображается в виде точки или в виде вектора изображается в виде точки или в виде вектора  на комплексной плоскости на комплексной плоскости  координатами координатами 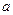 и и  . Такая запись числа . Такая запись числа  в виде точки (или вектора) называется декартовой (или векторной ) формой его записи. Числа в виде точки (или вектора) называется декартовой (или векторной ) формой его записи. Числа  и и  называются комплексно-сопряженными (см. рис. 1). называются комплексно-сопряженными (см. рис. 1).
Рис. 1
Модулем комплексного числа Аргументом комплексного числа Любое ненулевое комплексное число
где
При умножении комплексных чисел их модули перемножаются, а аргументы складываются. При делении комплексных чисел их модули делятся друг на друга, а аргументы вычитаются. Если
т.е. при возведении комплексного числа в степень Определение. Корнем n-ой степени из комплексного числа Теорема. Корней
где
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 , (3.3)
, (3.3) является решением ОЛДУ (3.3), С – число, то функция
является решением ОЛДУ (3.3), С – число, то функция  также является решением этого уравнения.
также является решением этого уравнения. являются решениями ОЛДУ (3.3), то их сумма также является решением уравнения (3.3).
являются решениями ОЛДУ (3.3), то их сумма также является решением уравнения (3.3). являются решениями ОЛДУ (3.3), то их линейная комбинация
являются решениями ОЛДУ (3.3), то их линейная комбинация
 , определенные на интервале
, определенные на интервале  , называются линейно независимыми на этом интервале, если соотношение
, называются линейно независимыми на этом интервале, если соотношение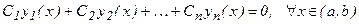 (3.4)
(3.4) (т.е. если это соотношение не выполняется для отличных от нуля чисел
(т.е. если это соотношение не выполняется для отличных от нуля чисел  ). Система n функций
). Система n функций  называется линейно зависимой на
называется линейно зависимой на 

 .
. , (3.5)
, (3.5)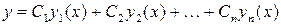 (3.6)
(3.6) , квадрат которого равен -1, т.е.
, квадрат которого равен -1, т.е.  .
.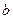 действительные числа, а
действительные числа, а  и
и  соответственно.
соответственно. , то
, то  , то
, то  называется мнимым числом.
называется мнимым числом.
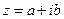 называется модуль (длина) вектора изображающего это число на комплексной плоскости, т.е.
называется модуль (длина) вектора изображающего это число на комплексной плоскости, т.е.  .
.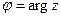 между положительным направлением действительной оси и вектором изображающим
между положительным направлением действительной оси и вектором изображающим  можно записать в виде
можно записать в виде ,
, . Эта запись называется тригонометрической формой записи числа
. Эта запись называется тригонометрической формой записи числа  Рис. 2
Рис. 2 , а
, а  - целое число, то
- целое число, то ,
, , что
, что  .
. ,
, . Здесь
. Здесь  – значение арифметического корня.
– значение арифметического корня.


