Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №1. Изучение среды программного пакета VisSimСодержание книги
Поиск на нашем сайте
Лабораторная работа №1. Изучение среды программного пакета VisSim Цель работы: приобретение навыков работы с моделирующим программным пакетом VisSim. Задание на лабораторную работу 1.1. Выяснить порядок запуска используемого программного пакета VisSim. 1.2. Просмотреть демонстрацию работы программы VisSim (файл csd_new.scm - control system design demo). Выявить: а) назначение программы; б) основные этапы работы с программой. 1.3. Запустить программу VisSim. Ознакомиться с содержанием меню. 1.4 Загрузить файл rlc.vsm с моделью "RLC"-цепи и изучить модель. Записать уравнение модели. Определить параметры моделируемых элементов и начальные условия в схеме. Изменить начальные условия и параметры модели по собственному усмотрению. 1.5. По варианту, указанному преподавателем, спроектировать модели источников периодического сигнала. Измерить и при необходимости компенсировать постоянную составляющую в сигнале. Использовать блок "plot" для осциллографирования. 1.6 Ознакомиться с моделями единичной ступенчатой функции - 1(t) и дельта-функции - 1'(t) (файл zvenya.vsm). Выявить положенные допущения (неидеальности) в моделях. 1.7 Выполнить исследование типовых динамических звеньев. По ходу работы необходимо изменить постоянные времени, коэффициенты затухания и усиления по своему усмотрению. Убедиться, что дифференцирование переходной функции звена дает его функцию веса и, наоборот, интегрирование функции веса звена дает его переходную функцию.
Требования к содержанию отчета Отчет по работе должен содержать: - краткое описание принципов функционирования программного пакета VisSim; - распечатки выполнения всех пунктов экспериментальной части и текстовые пояснения к ним. Для модели "RLC"-цепи записать уравнение, подставить в него параметры элементов и начальные условия, а также полностью охарактеризовать переходный процесс. - привести названия и графики использованных типовых возмущающих воздействий. Описать изменения в реакции типовых звеньев на варьирование параметров воздействий. - для каждого звена привести: а) название звена; б) структурную схему (подписав входную величину, выходную, сигнал ошибки и обратной связи); - вывод передаточной функции (подставить коэффициенты усиления и постоянные времени;
- проверить соответствие с линеаризованной передаточной функцией, которую рассчитывает программа VisSim (Analyze, Transfer Function Info); - записать координаты корней и полюсов функции); - привести список параметров с описанием характера влияния (на ЛАЧХ & ЛФЧХ, переходные процессы), переходную функцию, функцию веса; - привести графики ЛАЧХ и ЛФЧХ; диаграмму Найквиста; корневой годограф; - указать на неидеальности, присущие свойствам, которыми обладают реальные дифференцирующие устройства и их компьютерные дискретные модели. Пояснить причину неидеальности в дискретных моделях. - необходимо привести схемы проведения измерений (включая источники тест-сигналов) и дать пояснения к ним.
Варианты заданий Таблица
1.4 Контрольные вопросы 1.4.1 Объясните назначение пакета VisSim. 1.4.2 Расскажите о принципах функционирования пакета. 1.4.3 Как реализуются единичные ступенчатая функция и дельта-функция? 1.4.4 Как настраиваются параметры и начальные условия в схемах?
Задание на выполнение лабораторной работы 2.3.1 По варианту, указанному преподавателем, собрать схему рисунка 1.1. 2.3.2 Вывести на осциллограмму показания точек №1, №2, №3, №4 и зафиксировать при различных комбинациях (записать). 2.3.3 Исследовать динамику переходных процессов при изменении одного из параметров: А1, А2, А3. 2.3.4 Собрать схему для моделирования системы линейных дифференциальных уравнений. При этом для аij выбрать два произвольных значения в пределах от 0 до 10. 2.3.5 Вывести на осциллограмму координаты f, 2.3.6 В качестве воздействия использовать ступенчатую функцию с коэффициентом усиления k = 5 (f1) и синусоиду с частотой 5 Гц и амплитудой а=5( 2.3.7 Зафиксировать переходные процессы при различных значениях аij и воздействиях f1 и f2. Если переходный процесс будет расходящимся, необходимо изменять знак перед сумматором. Выполнить исследование типовых звеньев. Для каждого звена: 2.3.8 Составить структурную схему в среде VisSim.
2.3.9 Для коэффиценнтов усиления (1;5;10) и постоянных времени (1;5;10) определить: - кординаты корней и функции; - аналитическое выражение переходной функий - функции веса 2.3.10 Для единичной ступенчатой функции 2.3.11 Подать на вход типового звена гармонический сигнал Зафиксировать как входной, так и выходной сигнал; 2.3.12 Определить значение амплитуды и сдвига фазы при фиксированной амплитуде входного сигнала и построить график 2.3.13 Определить полосу пропускания диапазона частот, когда коэффициент усиления звена остается постоянным. 2.3.14 Получить подтверждение, что изменение коэффициента усиления вне полосы пропускания за одну декаду составляет либо 20дБ (10 раз), либо 40дб (100 раз).
Требования к отчету Отчет по работе содержит: - задание на лабораторную работу; - исследуемые схемы; - результаты исследований при конкретных значениях параметров и начальных условиях.
2.5 Контрольные вопросы 2.5.1 Как влияют параметры модели А1, А2. А3, а11, а12,…, а33 на вид переходного процесса? 2.5.2 Объясните различие в переходных процессах по п.2.3.7. 2.5.3 Объясните методику снятия частотной характеристики типовых звеньев.
Задание на лабораторную работу На моделях системы изучите принципы управления и влияние обратных связей в системах управления.
3.1.1 Принцип разомкнутого управления; Реализуйте модель системы в программном пакете VisSim (см. рисунок 3.1).
Рисунок 3.1 - Структурная схема САУ с разомкнутым управлением На рисунке 3.1 При заданных значениях K2=2, K3=4, T2=0.04, T3=0.5 определите K1, при котором yуст=2. Быстрота и характер переходного процесса y(t) обеспечивается выбором постоянных времени T2, T3, пронаблюдайте это. Выбором T2, T3 обеспечьте минимальное время переходного процесса.
3.1.2 Принцип компенсации; Структурная схема САУ в этом случае имеет следующий вид (см. рисунок 3.2)
Рисунок 3.2 - Схема САУ компенсации
Здесь: Wк(p) – звено компенсации (компенсатор). Для данной схемы проведите два эксперимента: - при отсутствии компенсатора и наличии сигналов g(t)=1(t) f(t)=0.5*1(t) зафиксируйте y(t)=1(t)* K1* W2(p)* W3(p)+0.5*1(t)* W3(p); - при наличии компенсатора и сигналов g(t)=1(t) f(t)=0.5*1(t) зафиксируйте y(t)=1(t)* K1* W2(p)* W3(p)+0.5*1(t)* W3(p)- 0.5*1(t)* Wk(p)* W2(p)* W3(p). Для второго эксперимента полная компенсация f(t) может быть достигнута, если будет выполнено условие f(t)*W3(p)=f(t)*Wk(p)*W2(p)* W3(p), откуда При реализации принципа компенсации существуют две основные проблемы: - необходимо измерять возмущение f(t); - необходимо вводить производные от возмущения.
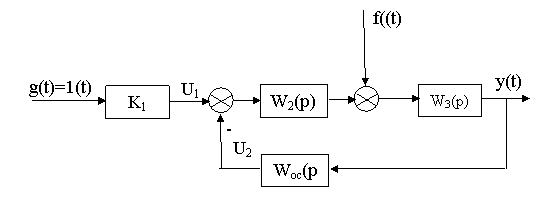
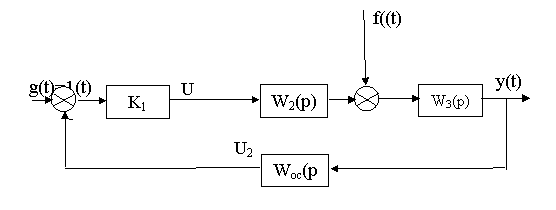
3.1.3 Принцип обратной связи; регулирование по отклонению: Ссоберите схему по рисунку 3.3.
Рисунок 3.3 - САУ с обратной связью
Согласно этой схеме коррективы в алгоритм управления вносятся по фактическому значению координат в системе. Для этой цели вводятся элементы для измеренияy(t) и выработки корректирующих воздействий U2(t) на управляющее устройство (цепь обратной связи); - зафиксируйте график y(t) без обратной связи:
- зафиксируйте график y(t) с обратной связью: Конечное выражение для y(t): Как видно из последнего выражения, увеличение, например, коэффициента обратной связи Кос уменьшает влияние возмущения на y(t), однако, и уменьшает действие управляющего сигнала U1=g(t)* К1.
3.1.4 Замкнутые системы с управлением по отклонению координат Широко распространены замкнутые системы с управлением (регулированием) по отклонению координат y(t) от заданных алгоритмом функционирования g(t). Структурная схема САР в таком случае имеет вид как на рисунке 3.4.
Рисунок 3.4 - САУ с регулированием по отклонению
Выполните следующее: - соберите схему САУ на рисунке 3.4 с численными значениями из п. в; - зафиксируйте переходный процесс y(t) и установившееся значение yуст(t); - зафиксируйте график y(t) с отключенной обратной связью Wос(p)=Кос=1. Сравните оба эксперимента; - в схеме на рисунке 3.4 замените д) управление с использованием совместно принципа регулирования по отклонению и принципа компенсации; структурная схема такой САР имеет следующий вид (см.рисунок 3.5). Выполните следующее: - соберите модель САУ на рисунке 3.5 при - зафиксируйте процесс y(t) на выходе модели САУ при отсутствии компенсирующего устройства и при наличии двух воздействий g(t) и f(t): Условие компенсации возмущения в этом случае а выходной сигнал
Рисунок 3.5 - САУ с регулированием по отклонению и с принципом компенсации
Требования к содержанию отчета 3.2.1 По каждому принципу управления представьте в соответствии с заданиями: графики переходных процессов с указанием масштабов и установившиеся значенияyуст. 3.2.2 Укажите выявленные особенности переходных процессов и установившихся значений выходной величины y(t) на изученных моделях САУ. 3.3 Контрольные вопросы 3.3.1 Расскажите об основных принципах управления. 3.3.2 Возможно ли перерегулирование в схеме по принципу разомкнутого управления? 3.3.3 Какие основные проблемы существуют при реализации принципа компенсации? 3.3.4 Какова роль U2(t) в схеме на рисунке 3.3? 3.3.5 Назначение компенсатора.
Задание на лабораторную работу 4.3.1 Составить передаточные функции W (p) для всех блоков структурных схем рабочих файлов. 4.3.2 Кратко описать назначение и принцип действия электронных схем приведенных на рис.
4.3.3. Изучить параметры сигнала задания g (t) в файле open.vsm. (определить интервалы, где координата задания постоянна, меняется с постоянной скоростью или с постоянным ускорением). 4.3.4 Включая каналы типового ПИД-регулятора по очереди, изучить, как формируется сигнал воздействия на объект — u (t) из первичной информации — x (t) (файл open.vsm). 4.3.5 В файлах open.vsm и closed.vsm коэффициенты усиления регуляторов оптимально настроены для управления объектом в соответствии с принципами Понселе (без ОС) и Ползунова-Уатта (с ОС). По своему усмотрению изменить параметры объекта и вновь настроить регуляторы. 4.3.6. Оценить степень влияния изменений параметров объекта на ошибку регулирования для обоих вариантов управления. При анализе следует учесть, что статическую составляющую ошибки определяет нестабильность коэффициента усиления объекта, а динамическую — его постоянная времени. 4.3.7 Изучить реализацию ПИД-регулятора на ОУ (файл pid.ca4).
Требования к содержанию отчета Отчет по работе должен содержать: - общее описание типового П, ПИ и ПИД-регуляторов (структурные схемы, дифференциальные уравнения или передаточные функции, основные параметры); - описание принципиальных отличий в формировании сигнала воздействия на объект u (t) каналами типового ПИД-регулятора (сравнительный анализ): а) при малых возмущениях в первичной информации x (t), и при больших; б) при постоянстве входной координаты, при движении её с постоянной скоростью и с постоянным ускорением. Привести поясняющие графические зависимости; - переходные процессы: а) при оптимальных настройках регуляторов для разных принципов регулирования объектом; б) для тех же случаев, с теми же настройками, но при отклонениях параметров объекта; дать пояснения; - два семейства зависимостей приведенной статической погрешности от изменения коэффициента усиления объекта при разных коэффициентах передачи пропорционального канала регулятора. В первом случае — для управления с ОС, во втором — без ОС. Первое семейство погрешностей привести к сигналу задания 1(t), второе — к среднему значению коэффициента усиления для каждой вариации (семейство вырождается в один график). Пояснить результаты; - определение для модели П, ПИ и ПИД-регулятора на ОУ коэффициентов усиления каждого канала. Для интегрального и дифференциального каналов необходимо указать граничные (сопрягающие) частоты или соответствующие постоянные времени. Нанести значения параметров на ЛАЧХ & ЛФЧХ регулятора. Выявить соответствие между параметрами и элементами схемы. Описать, какие ограничения накладывает частотная характеристика типового ОУ на параметры ПИД-регулятора. Продемонстрировать изменения сдвига фаз сигналов на характерных участках частотных характеристик, используя сигнал синусоидальной формы. При выполнении экспериментов следует учитывать, что данный ПИД-регулятор инвертирует сигнал.
4.6. Контрольные вопросы 4.6.1. Объясните появление статической ошибки при П – законе регулирования.
4.6.2. Поясните достоинства и недостатки линейных законов регулирования.
Задание на лабораторную работу 5.1 По передаточной функции разомкнутой системы записать ее характеристический полином D(p), определить его коэффициенты, выделить мнимую и вещественную составляющие. 5.2 Без применения программных инструментов построить асимптотические ЛАЧХ & ЛФЧХ для передаточных функций: 5.3 Для передаточных функций W(p) (файл nyquist.vsm) вывести передаточные функции соответствующих замкнутых систем Ф(p). 5.4 Исследовать границу устойчивости (типы границы устойчивости), используя возможности пакета VisSim: - задать передаточную функцию с помощью перечисления корней (нулей и полюсов её числителя и знаменателя); - убедиться, что только корни-полюсы с неотрицательной вещественной частью приводят к расходящемуся переходному процессу; - исследовать влияние корней характеристического полинома на вид годографа Михайлова (файл mihaylo4.vsm); - изучить влияние контурного коэффициента усиления на устойчивость системы и вид годографа Михайлова; 5.5 Задавая постоянную времени T2 (по варианту), подбором найти коэффициент усиления системы, при котором она будет находиться на колебательной границе устойчивости. В качестве признака границы использовать критерий Михайлова. 5.6 Для произвольно спроектированных передаточных функций привести переходные процессы, соответствующие наличию: а) одного и двух нулевых корней-полюсов; б) паре чисто мнимых корней-полюсов; в) корню-полюсу с положительной вещественной частью. 5.7 Продемонстрировать влияние коэффициента усиления на вид переходных процессов и вид годографа Михайлова.
Требования к содержанию отчета Отчет по работе должен содержать выполнение п.п.4.1-4.2 и распечатки по остальным пунктам задания. Варианты заданий Таблица
5.4 Контрольные вопросы 5.4.1 Объясните влияние коэффициента усиления на вид переходного процесса и вид годографа Михайлова. 5.4.2 Опишите с точки зрения удобства применения в исследованиях годографы Михайлова и Найквиста.
Список литературы 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.:Наука, 2005 г. 2. Сборник задач по теории автоматического регулирования и управления. Под ред. Бесекерского. – М.:Наука, 1978. 3. Теория автоматического регулирования. Под ред. А.А. Воронова. - М.: «Высшая школа», 1986. 4. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – М.: Профессия, 2003 5. Яковлев В.Б. Теория систем автоматического управления. – М.: Высшая школа, 2003. 6. Душин С.Е. Теория систем автоматического управления. – М.: Высшая школа, 2003. 7. Соломенцев Ю.М. Теория систем автоматического управления. – М.: Высшая школа, 2003. 8. Методы классической современной теории автоматического управления. Под ред. К.А. Пупкова. В 5 ти – томах. - М.: Высшая школа, 2004.
Содержание
Лабораторная работа №1. Изучение среды программного пакета VisSim Цель работы: приобретение навыков работы с моделирующим программным пакетом VisSim. Задание на лабораторную работу 1.1. Выяснить порядок запуска используемого программного пакета VisSim. 1.2. Просмотреть демонстрацию работы программы VisSim (файл csd_new.scm - control system design demo). Выявить: а) назначение программы; б) основные этапы работы с программой. 1.3. Запустить программу VisSim. Ознакомиться с содержанием меню. 1.4 Загрузить файл rlc.vsm с моделью "RLC"-цепи и изучить модель. Записать уравнение модели. Определить параметры моделируемых элементов и начальные условия в схеме. Изменить начальные условия и параметры модели по собственному усмотрению. 1.5. По варианту, указанному преподавателем, спроектировать модели источников периодического сигнала. Измерить и при необходимости компенсировать постоянную составляющую в сигнале. Использовать блок "plot" для осциллографирования. 1.6 Ознакомиться с моделями единичной ступенчатой функции - 1(t) и дельта-функции - 1'(t) (файл zvenya.vsm). Выявить положенные допущения (неидеальности) в моделях. 1.7 Выполнить исследование типовых динамических звеньев. По ходу работы необходимо изменить постоянные времени, коэффициенты затухания и усиления по своему усмотрению. Убедиться, что дифференцирование переходной функции звена дает его функцию веса и, наоборот, интегрирование функции веса звена дает его переходную функцию.
Требования к содержанию отчета Отчет по работе должен содержать: - краткое описание принципов функционирования программного пакета VisSim; - распечатки выполнения всех пунктов экспериментальной части и текстовые пояснения к ним. Для модели "RLC"-цепи записать уравнение, подставить в него параметры элементов и начальные условия, а также полностью охарактеризовать переходный процесс. - привести названия и графики использованных типовых возмущающих воздействий. Описать изменения в реакции типовых звеньев на варьирование параметров воздействий. - для каждого звена привести: а) название звена; б) структурную схему (подписав входную величину, выходную, сигнал ошибки и обратной связи); - вывод передаточной функции (подставить коэффициенты усиления и постоянные времени; - проверить соответствие с линеаризованной передаточной функцией, которую рассчитывает программа VisSim (Analyze, Transfer Function Info); - записать координаты корней и полюсов функции); - привести список параметров с описанием характера влияния (на ЛАЧХ & ЛФЧХ, переходные процессы), переходную функцию, функцию веса; - привести графики ЛАЧХ и ЛФЧХ; диаграмму Найквиста; корневой годограф; - указать на неидеальности, присущие свойствам, которыми обладают реальные дифференцирующие устройства и их компьютерные дискретные модели. Пояснить причину неидеальности в дискретных моделях. - необходимо привести схемы проведения измерений (включая источники тест-сигналов) и дать пояснения к ним.
Варианты заданий Таблица
1.4 Контрольные вопросы 1.4.1 Объясните назначение пакета VisSim. 1.4.2 Расскажите о принципах функционирования пакета. 1.4.3 Как реализуются единичные ступенчатая функция и дельта-функция? 1.4.4 Как настраиваются параметры и начальные условия в схемах?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.45.159 (0.014 с.) |

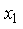 ,
, 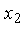 ,
, 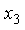 .
.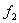 ).
).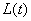 ;
;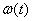 ;
;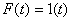 зафиксировать реальный переходный процесс (на осциллограмме вывести f (t); E (t); x (t).
зафиксировать реальный переходный процесс (на осциллограмме вывести f (t); E (t); x (t).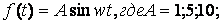
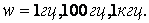
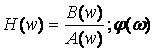
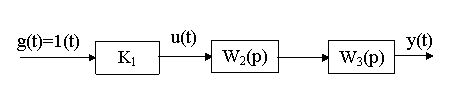
 . Близость y(t) к g(t) обеспечивается только конструкцией и подбором физических закономерностей, действующих во всех элементах. В модели это параметры K2, K3, T2, T3, а также параметр управляющего устройства (регулятора) - K1.
. Близость y(t) к g(t) обеспечивается только конструкцией и подбором физических закономерностей, действующих во всех элементах. В модели это параметры K2, K3, T2, T3, а также параметр управляющего устройства (регулятора) - K1.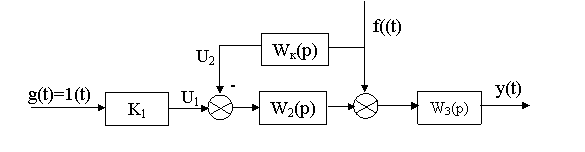
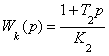 . Для рассматриваемого случая примите
. Для рассматриваемого случая примите 
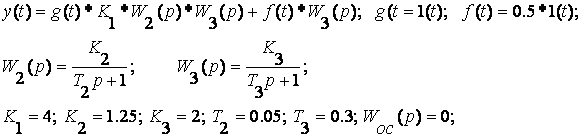
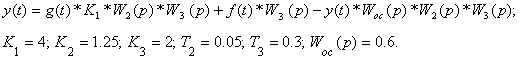
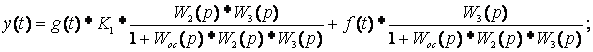
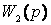 на
на 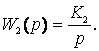 Если Кос=1, то yуст(t)=gуст(t)=1, т.е. в ней полностью компенсируется влияние возмущения f(t);
Если Кос=1, то yуст(t)=gуст(t)=1, т.е. в ней полностью компенсируется влияние возмущения f(t);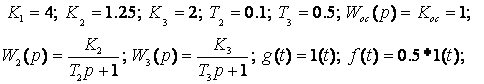

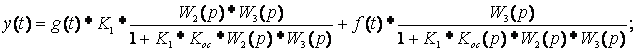 - зафиксируйте процесс y(t) на выходе модели САУ при наличии компенсирующего устройства с передаточной функцией
- зафиксируйте процесс y(t) на выходе модели САУ при наличии компенсирующего устройства с передаточной функцией 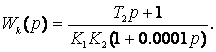
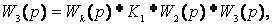
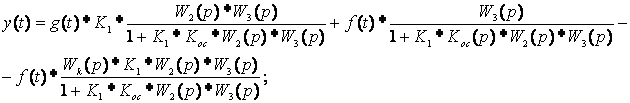 - сравните полученные результаты.
- сравните полученные результаты.