
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вторая теорема двойственности
Допустимое решение задачи (3.7) x*=(x*₁,…,xj*,…,xn*) и допустимое решение задачи (3.8) u*=(u₁*,…,ui*,…,um*) будут оптимальными для своих задач тогда и только тогда, когда для них выполняются «условия дополняющей нежесткости»(3.10) и (3.11). Первая группа условий дополняющей нежесткости (3.10) интерпретируется следующим образом. 1а. Если предельная эффективность ресурса под номером i больше нуля, т.е. ui0>0, то этот ресурс является лимитирующим или, иначе, полностью расходуется по данной оптимальной производственной программе x0=(x₁0,…,xj0,…,xn0), так как должно выполняться равенство ai₁x₁0+…+aijxj0+…+ainxn0=b 1б. Если ресурс под номером i не является лимитирующим для данной оптимальной производственной программы x0=(x₁0,…,xj0,…,xn0) или иначе, ai₁x₁+…+aijxj0+…+ainxn0<b, то предельная эффективность этого ресурса должна равняться нулю, т.е. ui0=0. Вторая группа условий дополняющей нежесткости (3.11) интерпретируется следующим образом. 2а. Если продукт под номером j выпускается по оптимальной производственной программе х0=(x₁0,...xj0,…,xn0), т.е. xj0>0, то суммарная эффективность всех затраченных ресурсов на выпуск единицы этого продукта должна равняться эффективность его реализации (цене продукта) a₁u₁0+…+aijui0+…+amjum0=cj 2б. Если суммарная эффективность всех затраченных ресурсов на выпуск единицы продукта под номером j превышает эффективность его реализации, т.е. a₁u1+…+aijui0+…+amjum0>cj, то продукт по оптимальной программе x0=(x₁0,...,xj0,…xn0) не должен производиться, т.е. xj0=0. Решение двойственной задачи
Составим и найдем решение двойственной задаче к задаче, решенной графическим и симплекс-методом. Прямая задача: Найти F(x) =16x₁+14x₂→max, при 0,8x₁+0,5x₂≤400 0,4x₁+0,8x₂≤365 x₁ - x₂≤100 x₂≤350 x₁, x₂ ≥0 Решение прямой задачи: x₁ =312,5кг; x₂=300кг F(x) =9200 руб. При этом первое и втрое ограничение превращается в строгое равенство, а третье и четвертое в строгое неравенство.
Двойственная задача: Найти Z (u) = 400u₁+365u₂+100u₃+350u₄→min при 0,8u₁+0,4u₂+u₃+0u₄≥16 0,5u₁+0,8u₂-u₃+u₄≥14 u₁ - u₄≥0
Относительно рассматриваемого варианта задач соответствующие условия “дополняющей нежесткости” первой и второй группы выглядит следующим образом.
u₁↔(400-0,8x₁-0,5x₂)=0; u₂↔(365-0,4x₁-0,8x₂)=0; (3.12) u3↔(100 - x1 + x2)= 0; u4↔(350 - x₂) =0.
x₁↔ (0,8u₁+0,4u₂+ u₃ -16)=0; (3.13) x₂↔ (0,5u₁+0,8u₂-u₃+u₄-14)=0; Из группы условий (3.12), так как 100-312,5+300=87,5>0 и 350-300=50>0 и на основе интерпретации 1б следует, что ограничения по спросу не лимитируют оптимальную программу, т.е. u₃=u₄=0 Из группы условий (3.13) на основе интерпретации 2а следует, что если оба продукта выпускаются по оптимальной программе, т.е. x*₁=312,5 и x*₂=300, то должны выполняться равенства 0,8u₁+0,4u₂+u₃=16 0,5u₁+0,8u₂-u₃+u₄=14 Из этих уравнений с учетом u₃=u₄=0 перейдем к решению следующей системы 0,8u₁+0,4u₂=16 0,5u₁+0,8u₂=14
Откуда получаем u ₁=
Z (u) =400 · В соответствие с вышесказанным найденное оптимальное решение позволяет уточнить понятие «теневая цена» это не просто цена, по которой мы будем продавать единицу того или иного ресурса. «Теневая цена» - это величина увеличения максимума целевой функции прямой задачи при изменении (увеличение) количества соответствующего ресурса на единицу, т.е.: u₁=16,36 - величина ожидаемого прироста максимума дохода (9200 руб.) от дополнительного вовлечения в производство 1 кг молока к имеющимся 400кг; u₂=7,27 руб.- величина ожидаемого прироста максимума дохода (9200 руб.) от дополнительного вовлечения в производство 1кг наполнителя к имеющимся 365 кг u₃=u₄=0 руб. - величина ожидаемого прироста дохода за счет увеличения спроса (недефицитные) ресурсы. В связи с этим «теневые цены» (u) в советской и российской литературе называются предельной эффективностью ресурса. Графическое решение двойственной задачи приведено на рис.3.13
40 A U2
35 30 25 20 15 10 7.27 B 5 U1 16.36 0 5 10 15 20 25 C30 35 40 Рис. 3.13 Графическое решение двойственной задачи Решение двойственной задачи также можно получить, используя последнюю итерацию симплекс-таблицы. Из первой теоремы двойственности следует, что U = C*A-1. Составим матрицу A из компонентов векторов, входящих в оптимальный базис
.
Определив обратную матрицу D = А-1 через алгебраические дополнения, получим:
Как видно из последнего плана симплексной таблицы, обратная матрица A-1 расположена в столбцах дополнительных переменных. Тогда U = C*A-1 =
Оптимальный план двойственной задачи равен: u1 = 16.36 u2 = 7.27 u3 = 0 u4 = 0 Z(U) = 400*16.36+365*7.27+100*0+365*0 = 9200
|
||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.125 (0.013 с.) |
 =(x₁, x₂), чтобы
=(x₁, x₂), чтобы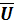 =(u₁,u₂,u₃,u₄), чтобы
=(u₁,u₂,u₃,u₄), чтобы (16,36) руб. и u₂=
(16,36) руб. и u₂= 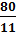 (7,27) руб., при этом
(7,27) руб., при этом +365·
+365· 


