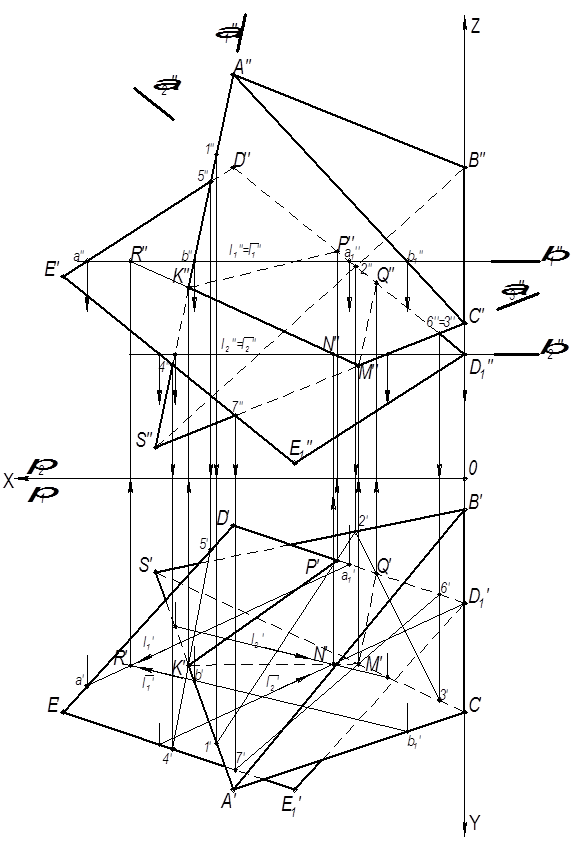Определение видимости ребер многогранника

СОДЕРЖАНИЕ

 

1.Цель и содержание расчётно-графической работы №1....................................4

2.Офомление графической работы........................................................................4

3.Решение задач эпюра...........................................................................................7

3.1.Построение исходных условий задачи...........................................................7

3.2.Определение видимости ребер многогранника..............................................9

3.3.Построение фигуры сечения............................................................................10

3.3.1.Пересечение призмы с треугольником.......................................................10

3.3.2.Пересечение пирамиды с параллелограммом............................................14

3.4.Определение видимости взаимного пересечения многогранника

и плоскости......................................................................................................16

4.Построение фигуры сечения методом замены плоскостей проекций..........18

5.Построение развёртки многогранника...........................................................22

Контрольные вопросы.........................................................................................25

Литература............................................................................................................26

 

 

1.Цель и содержание расчётно-графической работы №1

Цель работы – овладение способами решения позиционных задач на базе теоретического материала и приобретение навыков оформления графических работ.

Содержанием расчётно-графической работы №1 является:

1) построение линии пересечения многогранника с плоскостью;

2) построение развёртки многогранника.

Оформление графической работы

Работа выполняется на листах ватмана формата А3 (297х420 мм).

Каждый студент получает карточку индивидуального задания, где дано условие задачи и координаты точек в миллиметрах, по которым строятся фигуры.

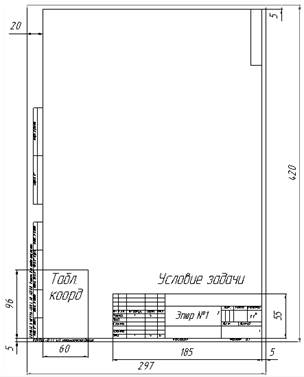
а Рис. 1. б

Рекомендуется предварительно решить задачу на тетрадном листе в клеточку или на миллиметровой бумаге в масштабе 1:1. Убедившись в правильности решения задачи, можно приступать к выполнению ее на ватмане указанного формата с соблюдением требований следующих государственных стандартов (ГОСТ):

1. ГОСТ 2.301 – Форматы;

2. ГОСТ 2.302 – Масштабы;

3. ГОСТ 2.303 – Линии;

4. ГОСТ 2.304 – Шрифты чертежные;

5. ГОСТ 2.104 – Основные надписи.

На рис.1 (а) показано оформление формата при его вертикальном расположении. Расчётно-графическая работа №1 может выполняться и при горизонтальном расположении формата, при этом основная надпись должна быть выполнена вдоль его длинной стороны (рис 1б).

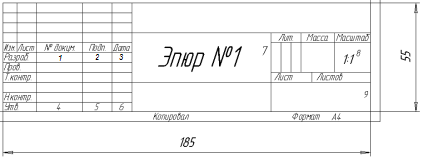
В правом нижнем углу обозначить прямоугольником место 55х185 мм для основной надписи. Образец основной надписи приведен на рис.2. Надпись включает следующие графы:

1. фамилия студента;

2. подпись студента;

3. дата выполнения эпюра;

4. фамилия преподавателя;

5. подпись преподавателя;

6. дата приема эпюра.

Рис. 2.

В левом нижнем углу формата обозначить прямоугольником место 60х96 мм для таблицы координат. Условие задачи расположить над основной надписью.

Все текстовые надписи и цифры на эпюре должны быть выполнены чертежным шрифтом (ГОСТ 2.304).

Графы 1 – 4 основной надписи заполняются шрифтом 3,5; графа 7 – шрифтом 10; графы 8,9 и условие задачи – шрифтом 7.

В графе 7 пишется название работы: Эпюр №1.

После оформления формата нужно наметить расположение фигур задачи в центре свободного поля чертежа. Масштаб изображения – 1:1. Необходимо сохранить на чертеже ход решения задачи, т.е. все линии и точки вспомогательных построений.

Для обводки эпюра рекомендуется карандаш марки «Конструктор», твердости «ТМ» или «М». Линии видимого контура фигур должны быть выполнены сплошной толстой основной линией толщиной S»0,6 мм, линии невидимого контура – штриховой линией толщиной S/2, т.е. S»0,3. Линии связи и вспомогательных построений – сплошной тонкой линией толщиной S/3, т.е. S»0,2 мм (ГОСТ 2.303).

После решения задачи необходимо окрасить видимые части заданной плоскости акварельной краской или цветными карандашами слабой интенсивности так, чтобы краска не закрыла линий вспомогательных построений. Участок фигуры сечения, находящийся внутри многогранника, особым цветом или штриховкой выделять не следует, т.к. он находится внутри призмы или пирамиды, которые считаем непрозрачными.

а Рис. 3. б

Точки вершин многогранника, заданной плоскости и найденной фигуры сечения следует обозначить прописными буквами латинского алфавита, шрифтом 7, точки вспомогательных построений – арабскими цифрами, шрифтом 5.

Построение комплексного чертежа требует большой точности и аккуратности, поэтому взаимно параллельные и перпендикулярные линии нужно строить с помощью двух угольников (рис.3а) или одного угольника и линейки (рис. 3б). При этом один угольник передвигается относительно другого, неподвижного, угольника или относительно неподвижной линейки.

 

Решение задач эпюра

В качестве задачи для выполнения эпюра №1 предлагается построить линию пересечения плоскости, заданной треугольником, с призмой или плоскости, заданной параллелограммом, с пирамидой.

Линия пересечения многогранника с плоскостью это, в общем случае, многоугольник, который ограничивает плоскую фигуру сечения.

Чтобы построить эту линию пересечения рекомендуется следующий план решения задачи:

I) построение чертежа условия задачи;

2) определение видимости ребер многогранника;

3) построение фигуры сечения;

4) определение видимости взаимного пересечения многогранника и плоскости.

Ниже рассматриваются примеры решения подобных задач различными способами.

 

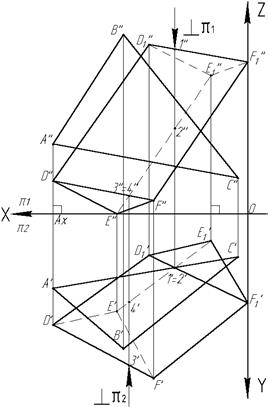
3.1.Построение исходных условий задачи.

Треугольная наклонная призма DEFD ₁ E ₁ F ₁ задается на эпюре проекциями одного основания – треугольника DEF - и проекциями одного бокового ребра DD ₁.

Построение начинаем с проведения и обозначения осей проекций и начала координат - точки 0. Рассмотрим построение проекций одной точки, например, точки А (рис. 4). Пo оси Х, влево от начала координат, откладываем в миллиметрах координату х точки А. Через полученную точку А_х проводим линию связи, перпендикулярную к оси Х, и откладываем на ней вниз от точки А_х координату у точки А (параллельно оси У). Таким образом получаем горизонтальную проекцию точки А¢, и вверх от точки А_х откладываем координату z точки А (параллельно оси Z) - получаем фронтальную проекцию А".

Аналогично строятся проекции остальных заданных точек, которые объединяются в отдельные фигуры.

 

Рис. 4. Рис. 5.

 

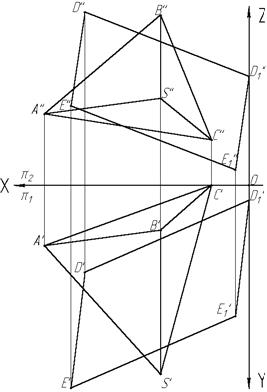
Построив основание призмы - треугольник DEF и ребро DD ₁, строим недостающие ребра EE ₁ и FF ₁, используя параллельность и равенство соответствующих ребер призмы.

Получив проекции точек E ₁ и F ₁, строим второе основание призмы – треугольник. D ₁ E ₁ F ₁. Построение проекций этих точек показано на рис. 4.

Необходимо сделать проверку точности построений. Она будет заключаться в том, что проекции каждой точки будут лежать на одной линии связи, перпендикулярной к оси проекции ОХ.

Таким образом, на комплексном чертеже будут представлены две проекции каждой фигуры: треугольника и призмы.

Треугольная наклонная пирамида (второй вариант задания) задается на эпюре проекциями вершины S и основания – треугольника ABC. На рис.5 дан комплексный чертеж пирамиды и параллелограмма DED ₁ E ₁. Параллелограмм задается двумя сторонами DD ₁ и DE. Другие две его стороны строятся из условия равенства и параллельности их заданным сторонам.

Для проверки правильности сделанных построений следует убедиться, что точки E ¢₁ и E ¢¢₁ лежат на линии связи, перпендикулярной к оси ОХ.

 

Построение фигуры сечения

Задача на построение линии пересечения поверхности многогранника с плоскостью является позиционной. И решить ее можно двумя способами. Первый способ состоит в многократном решении основной позиционной задачи на пересечение прямой с плоскостью. Достаточно найти точки пересечения ребер призмы с плоскостью треугольника, или, наоборот, точки пересечения сторон треугольника с гранями (плоскостями) призмы. Последовательно соединяя полученные точки отрезками прямых, получим линию пересечения призмы с треугольником.

Второй способ состоит в последовательном, многократном решении задачи на построение линии пересечения двух плоскостей, а именно, плоскости треугольника с плоскостью одной из граней призмы, затем плоскости того же треугольника с плоскостью другой грани призмы, и т.д.

Рассмотрим решение задачи для обоих вариантов задания.

 

И плоскости

При определении видимости фигур выбираются несколько пар скрещивающихся прямых. В каждой паре одна из прямых должна принадлежать одной фигуре, например, многограннику, другая прямая – второй фигуре, т.е. плоскости.

Например, на рис.6 для определения видимости на фронтальной плоскости проекций рассматриваем скрещивающиеся прямые A¢¢C¢¢ и F¢¢F ₁ ¢¢, используя конкурирующие точки 1¢¢ и 6¢¢. Проведем линии связи из этих точек на p₁, где видно, что по направлению взгляда перпендикулярно p₂ точка 1¢, принадлежащая прямой F¢F ₁ ¢, находится ближе к наблюдателю, чем точка 6¢, принадлежащая прямой А¢С¢. Это значит, что прямая F¢¢F ₁ ¢¢ будет на плоскости p₂ изображаться как видимая (сплошной толстой линией), а прямая А¢¢С¢¢ в этом месте – невидимая (штриховой линией).

Аналогично для определения видимости на горизонтальной плоскости проекций рассматриваем скрещивающиеся прямые A¢C¢ и F¢F ₁ ¢, используя конкурирующие точки 7¢ и 8¢. Проведем тонкую линию связи из этих точек на p₂, где видно, что по направлению взгляда перпендикулярно p₁ точка 8¢¢, принадлежащая прямой F¢¢F ₁ ¢¢, лежит выше, чем точка 7¢¢, принадлежащая прямой А¢¢С¢¢. Следовательно, в этом месте на плоскости p₁ прямая F¢F ₁ ¢ проходит над прямой А¢С¢, т.е. она видимая и будет изображаться основной сплошной толстой линией, а прямая А¢С¢ – невидимая и будет изображаться штриховой линией.

Таким образом, применяя конкурирующие точки, у которых одна пара проекций совпадает, а другая – нет, можно определить видимость фигур в любом месте чертежа (см.рис.9).

Следует помнить, что до решения задачи необходимо определить видимость ребер многогранника, а в конце решения – видимость фигуры сечения и плоскости (треугольника или параллелограмма) вместе и с учетом этого закрасить видимую часть заданной плоскости.

Пример оформления расчётно-графической работы на рис. 11.

Рис. 9.

 

Рис. 13

 

Рис. 14.

Рис. 15.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. Почему одна проекция не определяет положение точки в пространстве?

2. Как по двум заданным проекциям точки построить третью?

3. Под каким углом к оси проекции должны проходить линии связи?

4. Где расположена сама точка, заданная своими проекциями?

5. Как задается на чертеже прямая линия?

6. Какие виды прямых частного положения Вы знаете?

7. Как изображаются на чертеже прямые уровня: горизонталь, фронталь, профильная прямая?

8. Как изображаются на чертеже проецирующие прямые?

9. Как построить проекции отрезков, которые делят прямую линию в заданном отношении (теорема Фаллеса)?

10. Какие взаимные положения двух прямых Вы знаете?

11. Укажите условие, при котором две прямые пересекаются.

12. Укажите условие, при котором две прямые являются скрещивающимися.

13. Какие две точки называются конкурирующими?

14. Как определить видимость на чертеже при помощи конкурирующих точек?

15. Какими способами можно задать плоскость на чертеже?

16. Что такое плоскость общего положения?

17. Какие виды плоскости частного положения Вы знаете?

18. Каков порядок графических построений при определении линии пересечения двух плоскостей?

19. Какие виды взаимных положений прямой и плоскости Вы знаете?

20. Каков порядок графических построений при определение точки пересечения прямой с плоскостью?

 

ЛИТЕРАТУРА

 

1. Гордон В.О., Семнцов-Огиевский М.А. Курс начертательной геометрии, М.: Высш. шк., 2002.-272 с: ил.

2. Гордон В.О., Иванов Ю.Б., Солнцева Т.Е. Сборник задач по курсу начертательной геометрии, М.: Высш. шк., 1998.-320 с: ил.

3. Локтев О.В. Краткий курс начертательной геометрии. М.: Высш. шк., 2002

4. Начертательная геометрия/ Крылов Н.Н. и др. - М.: Высш. шк., 2000

5. Фролов С.А., Начертательная геометрия: Учебник для втузов. М.: Машиностроение, 1983. – 240 с., ил

6. ЕСКД. Основные положения. ГОСТ 2.104-68. Основные надписи. М.: Изд-во стандартов, 2001, 343с.

7. ЕСКД. Общие правила выполнения чертежей. ГОСТ 2.301-68 – ГОСТ 2.304-81. М.: Изд-во стандартов, 2001, 238с.

СОДЕРЖАНИЕ

 

1.Цель и содержание расчётно-графической работы №1....................................4

2.Офомление графической работы........................................................................4

3.Решение задач эпюра...........................................................................................7

3.1.Построение исходных условий задачи...........................................................7

3.2.Определение видимости ребер многогранника..............................................9

3.3.Построение фигуры сечения............................................................................10

3.3.1.Пересечение призмы с треугольником.......................................................10

3.3.2.Пересечение пирамиды с параллелограммом............................................14

3.4.Определение видимости взаимного пересечения многогранника

и плоскости......................................................................................................16

4.Построение фигуры сечения методом замены плоскостей проекций..........18

5.Построение развёртки многогранника...........................................................22

Контрольные вопросы.........................................................................................25

Литература............................................................................................................26

 

 

1.Цель и содержание расчётно-графической работы №1

Цель работы – овладение способами решения позиционных задач на базе теоретического материала и приобретение навыков оформления графических работ.

Содержанием расчётно-графической работы №1 является:

1) построение линии пересечения многогранника с плоскостью;

2) построение развёртки многогранника.

Оформление графической работы

Работа выполняется на листах ватмана формата А3 (297х420 мм).

Каждый студент получает карточку индивидуального задания, где дано условие задачи и координаты точек в миллиметрах, по которым строятся фигуры.

а Рис. 1. б

Рекомендуется предварительно решить задачу на тетрадном листе в клеточку или на миллиметровой бумаге в масштабе 1:1. Убедившись в правильности решения задачи, можно приступать к выполнению ее на ватмане указанного формата с соблюдением требований следующих государственных стандартов (ГОСТ):

1. ГОСТ 2.301 – Форматы;

2. ГОСТ 2.302 – Масштабы;

3. ГОСТ 2.303 – Линии;

4. ГОСТ 2.304 – Шрифты чертежные;

5. ГОСТ 2.104 – Основные надписи.

На рис.1 (а) показано оформление формата при его вертикальном расположении. Расчётно-графическая работа №1 может выполняться и при горизонтальном расположении формата, при этом основная надпись должна быть выполнена вдоль его длинной стороны (рис 1б).

В правом нижнем углу обозначить прямоугольником место 55х185 мм для основной надписи. Образец основной надписи приведен на рис.2. Надпись включает следующие графы:

1. фамилия студента;

2. подпись студента;

3. дата выполнения эпюра;

4. фамилия преподавателя;

5. подпись преподавателя;

6. дата приема эпюра.

Рис. 2.

В левом нижнем углу формата обозначить прямоугольником место 60х96 мм для таблицы координат. Условие задачи расположить над основной надписью.

Все текстовые надписи и цифры на эпюре должны быть выполнены чертежным шрифтом (ГОСТ 2.304).

Графы 1 – 4 основной надписи заполняются шрифтом 3,5; графа 7 – шрифтом 10; графы 8,9 и условие задачи – шрифтом 7.

В графе 7 пишется название работы: Эпюр №1.

После оформления формата нужно наметить расположение фигур задачи в центре свободного поля чертежа. Масштаб изображения – 1:1. Необходимо сохранить на чертеже ход решения задачи, т.е. все линии и точки вспомогательных построений.

Для обводки эпюра рекомендуется карандаш марки «Конструктор», твердости «ТМ» или «М». Линии видимого контура фигур должны быть выполнены сплошной толстой основной линией толщиной S»0,6 мм, линии невидимого контура – штриховой линией толщиной S/2, т.е. S»0,3. Линии связи и вспомогательных построений – сплошной тонкой линией толщиной S/3, т.е. S»0,2 мм (ГОСТ 2.303).

После решения задачи необходимо окрасить видимые части заданной плоскости акварельной краской или цветными карандашами слабой интенсивности так, чтобы краска не закрыла линий вспомогательных построений. Участок фигуры сечения, находящийся внутри многогранника, особым цветом или штриховкой выделять не следует, т.к. он находится внутри призмы или пирамиды, которые считаем непрозрачными.

а Рис. 3. б

Точки вершин многогранника, заданной плоскости и найденной фигуры сечения следует обозначить прописными буквами латинского алфавита, шрифтом 7, точки вспомогательных построений – арабскими цифрами, шрифтом 5.

Построение комплексного чертежа требует большой точности и аккуратности, поэтому взаимно параллельные и перпендикулярные линии нужно строить с помощью двух угольников (рис.3а) или одного угольника и линейки (рис. 3б). При этом один угольник передвигается относительно другого, неподвижного, угольника или относительно неподвижной линейки.

 

Решение задач эпюра

В качестве задачи для выполнения эпюра №1 предлагается построить линию пересечения плоскости, заданной треугольником, с призмой или плоскости, заданной параллелограммом, с пирамидой.

Линия пересечения многогранника с плоскостью это, в общем случае, многоугольник, который ограничивает плоскую фигуру сечения.

Чтобы построить эту линию пересечения рекомендуется следующий план решения задачи:

I) построение чертежа условия задачи;

2) определение видимости ребер многогранника;

3) построение фигуры сечения;

4) определение видимости взаимного пересечения многогранника и плоскости.

Ниже рассматриваются примеры решения подобных задач различными способами.

 

3.1.Построение исходных условий задачи.

Треугольная наклонная призма DEFD ₁ E ₁ F ₁ задается на эпюре проекциями одного основания – треугольника DEF - и проекциями одного бокового ребра DD ₁.

Построение начинаем с проведения и обозначения осей проекций и начала координат - точки 0. Рассмотрим построение проекций одной точки, например, точки А (рис. 4). Пo оси Х, влево от начала координат, откладываем в миллиметрах координату х точки А. Через полученную точку А_х проводим линию связи, перпендикулярную к оси Х, и откладываем на ней вниз от точки А_х координату у точки А (параллельно оси У). Таким образом получаем горизонтальную проекцию точки А¢, и вверх от точки А_х откладываем координату z точки А (параллельно оси Z) - получаем фронтальную проекцию А".

Аналогично строятся проекции остальных заданных точек, которые объединяются в отдельные фигуры.

 

Рис. 4. Рис. 5.

 

Построив основание призмы - треугольник DEF и ребро DD ₁, строим недостающие ребра EE ₁ и FF ₁, используя параллельность и равенство соответствующих ребер призмы.

Получив проекции точек E ₁ и F ₁, строим второе основание призмы – треугольник. D ₁ E ₁ F ₁. Построение проекций этих точек показано на рис. 4.

Необходимо сделать проверку точности построений. Она будет заключаться в том, что проекции каждой точки будут лежать на одной линии связи, перпендикулярной к оси проекции ОХ.

Таким образом, на комплексном чертеже будут представлены две проекции каждой фигуры: треугольника и призмы.

Треугольная наклонная пирамида (второй вариант задания) задается на эпюре проекциями вершины S и основания – треугольника ABC. На рис.5 дан комплексный чертеж пирамиды и параллелограмма DED ₁ E ₁. Параллелограмм задается двумя сторонами DD ₁ и DE. Другие две его стороны строятся из условия равенства и параллельности их заданным сторонам.

Для проверки правильности сделанных построений следует убедиться, что точки E ¢₁ и E ¢¢₁ лежат на линии связи, перпендикулярной к оси ОХ.

 

Определение видимости ребер многогранника

Поскольку призма и пирамида считаются непрозрачными фигурами, то необходимо определять видимость их ребер и граней. Для этого в каждом случае используются две конкурирующие точки, принадлежащие двум скрещивающимся прямым - ребрам.

Чтобы определить видимость ребер призмы (см. рис. 4) на горизонтальной плоскости проекций, обозначим на плоскости p₁ совпадающую пару конкурирующих точек I и 2, принадлежащих скрещивающимся прямым D ₁ F ₁ и EE ₁. Проведя линию связи от точек 1' = 2¢ вверх, отметим точку 1" нa D² ₁ F² ₁ и точку 2² на E ² E ²₁. Относительно плоскости p₁ точка 1 находится выше, чем точка 2, следовательно, на горизонтальной плоскости проекций точка 1 и отрезок D ₁ F ₁ видимы, а точка 2 и отрезок ЕE ₁ - невидимы.

Для определения видимости ребер призмы на фронтальной плоскости проекций обозначим на плоскости p₂ совпадающую пару конкурирующих точек 3 и 4, принадлежащих скрещивающимся прямым DF и EE ₁. Отметив 3 на DF и 4 на ЕЕ ₁, видим, что относительно плоскости p₂ точка 3 находится ближе к наблюдателю, чем точка 4, следовательно, на фронтальной плоскости проекций точка 3 и отрезок DF видимы, а точка 4 и отрезок ЕE ₁ - невидимы.

Таким образом, ребро будет невидимым на обеих плоскостях проекций. Проекции этого ребра следует изобразить штриховой линией, толщиной» 0,3 мм. Аналогично определяется видимость ребер пирамиды во втором варианте задания.

 

Построение фигуры сечения

Задача на построение линии пересечения поверхности многогранника с плоскостью является позиционной. И решить ее можно двумя способами. Первый способ состоит в многократном решении основной позиционной задачи на пересечение прямой с плоскостью. Достаточно найти точки пересечения ребер призмы с плоскостью треугольника, или, наоборот, точки пересечения сторон треугольника с гранями (плоскостями) призмы. Последовательно соединяя полученные точки отрезками прямых, получим линию пересечения призмы с треугольником.

Второй способ состоит в последовательном, многократном решении задачи на построение линии пересечения двух плоскостей, а именно, плоскости треугольника с плоскостью одной из граней призмы, затем плоскости того же треугольника с плоскостью другой грани призмы, и т.д.

Рассмотрим решение задачи для обоих вариантов задания.