
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учебник математики для шестого классаСодержание книги
Поиск на нашем сайте
М аленький мальчик, за которым я присматривал, был в шестом классе, и он хотел разобраться в одной конкретной математической задаче. Это была сравнительно простая задача, но я не помнил, как это делается. Чтобы вспомнить и объяснить ему, как она решается, я просмотрел его учебник. Просматривая учебник, я увидел нужную мне геометрию – в учебнике для шестого класса! Автор учебника не понимал того, что видел я, потому что его мысли тогда двигались в совсем другом направлении. Но я увидел в этой математике что-то такое, что искал, и это был ключ, связывающий воедино эти две первоначальные последовательности.
И мея круг с квадратным крестом внутри него, возьмём радиус диска за эталон и назовём её единицей: 1 (что очень облегчает расчёты). Вычерчивание концентрических кругов на таком же расстоянии друг от друга наружу от этого первого радиуса даёт вам полярный график. Спирали на Полярном графике
П редставьте, что этот маленький центральный круг есть планета в пространстве космоса. С поверхности планеты автор учебника по математике вычертил спираль Золотого Сечения – не Фибоначчи, но Золотого Сечения. Она начинается в нулевом радиусе на поверхности маленькой «планеты» в середине, и описывает один оборот, от нуля до 360 градусов, или назад к нулю (Рис.8-23). Т еперь, чтобы определить значение каждой точки спирали, вы используете средний круг в качестве единицы (поскольку он представляет расстояние от центра к первой окружности, которую мы назвали «планетой»), и затем отсчитываете единицы наружу до того места, где спираль пересекает радиус. Так, на радиусе в 260° (между четвёртым и пятым кругами) вы отсчитали наружу примерно 4,5. (Конечно, на компьютере вы можете сделать это точнее.) На радиальной линии в 210° спираль достигала почти 3,3. Все ли это поняли? Т еперь смотрите, что происходит с конкретными значениями от нуля до 360°. При нулевом градусе спираль находится точно на расстоянии одного круга (радиальное возрастание) от центра, поскольку она начинается с поверхности маленькой сферы или планеты. Затем она делает оборот, проходя через различные изменения до тех пор, пока не достигает 120°, где спираль пересекает второй круг. Она продолжает движение наружу к пересечению с четвёртым кругом точно там, где располагается радиальная линия 240°. И восьмого (внешнего) круга она дистигает точно у радиуса 360º (или 0°). Радиальные возрастания удваивались (бинарная последовательность 1,2,4,8) точно в 0°,120°,240° и 360°.
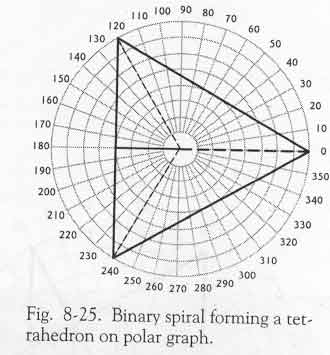
Я был так возбуждён, что несколько дней ходил колесом. Я знал, что обнаружил нечто действительно необычайное, хотя полностью ещё не понимал, что это такое. (Это одна из моих слабых сторон, в которой мне следует тут признаться. Однажды увидев это, я понял, что раз я расшифровал одну из закономерностей, это должно бы быть справедливо и для другой, но я никогда не возвращался к ней, чтобы хотя бы взглянуть на другую модель, которая, вероятно, так же интересна). Н о я в самом деле проанализировал, как ведёт себя бинарная последовательность. Спираль пересекается на 0°, 120°, 240° и 360°. Как видите, это даёт образование равнобедренного треугольника (Рис.8-25). Если бы эта бинарная спираль продолжала движение наружу, она пересекала бы радиусы в следующих возрастаниях по градусам 16, 32, 64 и так далее, однако всегда касалась бы этих трёх радиальных линий на 120, 240 и 360 градусах, так как они тоже продолжены. Т ут есть не только треугольник, но на самом деле вы глядите на трёхмерный тетраэдр, потому что радиусы 120, 240 и 360 градусов продолжаются к центру, образуя как план тетраэдра, так и его вид сбоку. Н овейшая информация: Была обнаружена ещё одна закономерность, которая, как я и подозревал, оказалась последовательностью Фибоначчи. Однако, я ещё не определил, какова значимость этого открытия для сознания.
|
||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.75.6 (0.006 с.) |

 Мне жаль, что я не помню ни названия книги, ни автора – это было давно – но там был показан полярный график и его отношение к спирали Золотого Сечения. Рис.8-21– это карта Южного полюса на полярнoм графике. Обратите внимание на крест, проходящий через центр, одна из линий следует оси х и другая следует оси у. В самом деле, эти линии пересекают каждый круг. Мы демонстрировали это, взяв плоский диск толщиной около половины дюйма, произвольно насыпая на него песок. Мы держали его за рукоятку, находящуюся под ним и ударяли по нему деревянным молоточком. Песок перераспределялся в совершенно квадратный крест, такой, как вы видите на этой иллюстрации. Если бы мы использовали звуковой генератор на диске, тогда песок перестраивался бы во множество других геометрических моделей. Но самой первой моделью, появляющейся при несильном ударе по круглому диску, будет идеальный квадратный крест.
Мне жаль, что я не помню ни названия книги, ни автора – это было давно – но там был показан полярный график и его отношение к спирали Золотого Сечения. Рис.8-21– это карта Южного полюса на полярнoм графике. Обратите внимание на крест, проходящий через центр, одна из линий следует оси х и другая следует оси у. В самом деле, эти линии пересекают каждый круг. Мы демонстрировали это, взяв плоский диск толщиной около половины дюйма, произвольно насыпая на него песок. Мы держали его за рукоятку, находящуюся под ним и ударяли по нему деревянным молоточком. Песок перераспределялся в совершенно квадратный крест, такой, как вы видите на этой иллюстрации. Если бы мы использовали звуковой генератор на диске, тогда песок перестраивался бы во множество других геометрических моделей. Но самой первой моделью, появляющейся при несильном ударе по круглому диску, будет идеальный квадратный крест.  Вот как обычно выглядит полярный график (Рис.8-22) с 36-тью радиальными линиями, включая сюда и вертикальную, и горизонтальную линии. Эти линии указывают 360° с десятиградусным возрастанием. Затем, нарисованы концентрические окружности, каждая на одинаковом расстоянии от предыдущей таким образом, вдоль каждого радиуса откладывая восемь равных отрезков, считая внутренний круг как первый. За полярным графиком кроется очень глубокий смысл. Прежде всего подумайте, что он представляет. Это двумерное изображение, где приводится попытка проекцией на плоскую поверхность показать трёхмерную сферу, одну из священных форм. Эта форма – тень. Отбрасываемые тени дают одну из священных возможностей получения информации. К тому же, полярный график составлен из как прямых линий (мужских) так и плавных линий (женских), наложенных друг на друга – мужская и женская энергии единовременно.
Вот как обычно выглядит полярный график (Рис.8-22) с 36-тью радиальными линиями, включая сюда и вертикальную, и горизонтальную линии. Эти линии указывают 360° с десятиградусным возрастанием. Затем, нарисованы концентрические окружности, каждая на одинаковом расстоянии от предыдущей таким образом, вдоль каждого радиуса откладывая восемь равных отрезков, считая внутренний круг как первый. За полярным графиком кроется очень глубокий смысл. Прежде всего подумайте, что он представляет. Это двумерное изображение, где приводится попытка проекцией на плоскую поверхность показать трёхмерную сферу, одну из священных форм. Эта форма – тень. Отбрасываемые тени дают одну из священных возможностей получения информации. К тому же, полярный график составлен из как прямых линий (мужских) так и плавных линий (женских), наложенных друг на друга – мужская и женская энергии единовременно. 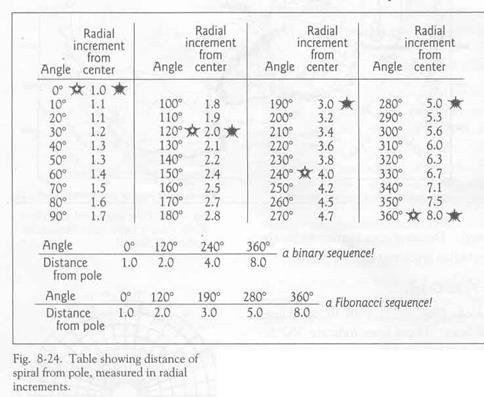
 Обратите внимание на Рис.8-24, где показаны точки пересечения спирали. Белые звёздочки слева от столбика радиального возрастания показывают, где бинарная последовательность пересекает радиус. Чёрные звёздочки показывают, как спираль развивается по последовательности Фибоначчи (1,2,3,5,8), пересекая радиусы 120°, 190°, 280° и 360°. Обе последовательности одновременно достигают полного круга (360°), хотя и по различной линии возрастания, следуя этой спирали Золотого Сечения. Эта спираль, показанная на Полярном графике, интегрировала последовательности Фибоначчи и бинарную!
Обратите внимание на Рис.8-24, где показаны точки пересечения спирали. Белые звёздочки слева от столбика радиального возрастания показывают, где бинарная последовательность пересекает радиус. Чёрные звёздочки показывают, как спираль развивается по последовательности Фибоначчи (1,2,3,5,8), пересекая радиусы 120°, 190°, 280° и 360°. Обе последовательности одновременно достигают полного круга (360°), хотя и по различной линии возрастания, следуя этой спирали Золотого Сечения. Эта спираль, показанная на Полярном графике, интегрировала последовательности Фибоначчи и бинарную! 


