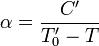Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа перемещения проводника с током в магнитном поле.Содержание книги
Поиск на нашем сайте Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. dФ – изменение магнитного потока. Работа силы Ампера на всем пути: A = I(Фn – Ф). 12.Контур с током в однородном и неоднородном магнитном поле. Неоднородное поле Если контур с током находится в неоднородном магнитном поле, то на него, помимо вращающего момента, действует также сила, обусловленная наличием градиента магнитного поля.
Согласно написанной формуле, сила, действующая на контур в неоднородном магнитном поле, зависит от взаимной ориентации векторов P и B. Если эти векторы параллельны, то сила положительна и контур будет втягиваться в область более сильного поля; если векторы B и P антипараллельны, то сила отрицательна и контур будет выталкиваться из поля. Работа силы Fx на элементарном перемещении dx равна убыли потонцеальной энергии Fxdx = - dWp Fx = dWp/dx = Pm dB/dx cos a. dB/dx = gradB – градиент вектора B. При а = 0 контур втягивается в поле, при а = 180 – выталкивается. Однородное поле Нормаль к контуру и. Если пустить ток возникнет магнитный момент, который развернет рамку. На рамку со стороны поля действует сила Ампера и эти силы будут действовать с этой и другой стороны рамки эти 2 силы равны по модулю и противоположно направлены, образуют пару сил и создают вращательный момент M=Fb, где b- один из размеров рамки. М = [Рм В] –механический момент.(в векторной форме). Мmax = I a b B = I S B = Pm B. Работа против сил поля для поворота на угол d; Wp = - Pm B cosa = -(PmB).
Магнитное поле в веществе Магнитное поле в веществе. Гипотеза Ампера о молекулярных токах. Намагниченность вещества. Свойство намагниченности вещества. Напряженность магнитного поля Все природные вещества в той или иной мере обладают магнитными свойствами, эти вещества называют магнетиками. Частными случаями магнетиков являются пара- и диамагнетики, ферромагнетики и антиферромагнетики... В начале исследования магнетизма для объяснения свойств постоянных магнитов Ампер выдвинул смелую по тем временам гипотезу о существовании так называемых "молекулярных токов", совокупность которых объясняет магнитные свойства вещества. В настоящее время гипотеза Ампера представляется чуть ли не очевидной, физические механизмы, ответственные за магнитные свойства веществ, изучены значительно более глубоко, чем это было возможно во времена Ампера. Магнитным свойством веществ посвящены многие специальные руководства. Рассмотрим достаточно малый объем вещества. Допустим, что суммарный магнитный момент молекулярных токов (магнитных диполей) в этом объеме равен .
В соответствии с определением намагниченность (вектор намагничения) Если магнитный момент элементарного молекулярного тока равен ,
где Совокупность элементарных молекулярных токов образует объемную плотность ) связаны с носителями зарядов, которые могут относительно свободно перемещаться по проводнику. Токи намагничения могут существовать и в непроводящей электрический ток среде.
Представить себе наглядно физическую связь между намагниченностью и токами намагничения можно, анализируя случай однородного распределения магнитных диполей одного направления Легко видеть, что внутри выделенного элемента вещества молекулярные токи компенсируют друг друга, некомпенсированным остается только ток по поверхности выделенного объема. Обратим внимание на то, что направление тока намагничения на перпендикулярно ориентации магнитных диполей, то есть вектору намагничения .
В случае неоднородного распределения магнитных диполей одного направления, например, показанного на, помимо поверхностных токов намагничения Рассмотрим поверхность ,
Где
Легко видеть, что для внутренних точек поверхности Если модуль отдельного магнитного диполя равен
где .
Основное свойство намагниченности
где
В этих соотношениях Заметим, что полученные соотношения являются следствием принятых за исходные определений. Циркуляция вектора магнитной индукции .
Анализируя совокупность соотношений, замечаем, что имеет место .
Полученная зависимость удобна тем, что в ее правой части стоит величина тока проводимости Введем в рассмотрение вектор напряженности магнитного
и получим интегральное соотношение ,
и соответствующее ему (следствие классической теоремы Стокса) дифференциальное соотношение
При феноменологическом подходе к описанию магнитной среды, не затрагивающем молекулярно-кинетическое строение среды, полагают, что ,
причем для многих веществ и "слабых" магнитных полей эта зависимость линейная и однородная: ,
где Зависимость позволяет записать "материальное уравнение" магнитной среды в форме , где
носит название "магнитная проницаемость" среды. Вопрос об объемной плотности некомпенсированных молекулярных токов решается прямым вычислением:
Легко видеть, что обусловлена токами проводимости и неоднородностью магнитных свойств среды. ВОПРОС 2 Классификация веществ по магнитным свойствам По реакции на внешнее магнитное поле и характеру внутреннего магнитного упорядочения все вещества в природе можно подразделить на пять групп: диамагнетики, парамагнетики, ферромагнетики, антиферромагнетики и ферримагнетики. Перечисленным видам магнетиков соответствуют пять различных видов магнитного состояния вещества: диамагнетизм, парамагнетизм, ферромагнетизм, антиферромагнетизм и ферримагнетизм. К диамагнетикам относят вещества, у которых магнитная восприимчивость отрицательна и не зависит от напряженности внешнего магнитного поля. К диамагнетикам относятся инертные газы, водород, азот, многие жидкости (вода, нефть и ее производные), ряд металлов (медь, серебро, золото, цинк, ртуть, галлий и др.), большинство полупроводников (кремний, германий, соединения А3В5, А2В6) и органических соединений, щелочно-галоидные кристаллы, неорганические стекла и др. Диамагнетиками являются все вещества с ковалентной химической связью и вещества в сверхпроводящем состоянии. К парамагнетикам относят вещества с положительной магнитной восприимчивостью, не зависящей от напряженности внешнего магнитного поля. К числу парамагнетиков относят кислород, окись азота, щелочные и щелочноземельные металлы, некоторые переходные металлы, соли железа, кобальта, никеля и редкоземельных элементов. К ферромагнетикам относят вещества с большой положительной магнитной восприимчивостью (до 106), которая сильно зависит от напряженности магнитного поля и температуры. Антиферромагнетиками являются вещества, в которых ниже некоторой температуры спонтанно возникает антипараллельная ориентация элементарных магнитных моментов одинаковых атомов или ионов кристаллической решетки. При нагревании антиферромагнетик испытывает фазовый переход в парамагнитное состояние. Антиферромагнетизм обнаружен у хрома, марганца и ряда редкоземельных элементов (Ce, Nd, Sm, Tm и др.). Типичными антиферромагнетиками являются простейшие химические соединения на основе металлов переходной группы типа окислов, галогенидов, сульфидов, карбонатов и т.п. К ферримагнетикам относят вещества, магнитные свойства которых обусловлены нескомпенсированным антиферромагнетизмом. Подобно ферромагнетикам они обладают высокой магнитной восприимчивостью, которая существенно зависит от напряженности магнитного поля и температуры. Наряду с этим ферримагнетики характеризуются и рядом существенных отличий от ферромагнитных материалов.Свойствами ферримагнетиков обладают некоторые упорядоченные металлические сплавы, но, главным образом, - различные оксидные соединения, среди которых наибольший практический интерес представляют ферриты. МАГНИТНАЯ ВОСПРИИМЧИВОСТЬ, величина, характеризующая связь намагниченности вещества с магнитным полем в этом веществе. М. в. в статич. полях равна отношению намагниченности вещества М к напряжённости Н намагничивающего поля:; - величина безразмерная. М. в., рассчитанная на 1 кг (или 1 г) вещества, наз. удельной (, где р - плотность вещества), а М. в. одного моля - молярной (или атомной):, где т - молекулярная масса вещества. С магнитной проницаемостью. в. в статич. полях (статич. М. в.) связана соотношениями: (в ед. СГС), (в ед. СИ). М. в. может быть как положительной, так и отрицательной. Отрицательной М. в. обладают диамагнетики (ДМ), они намагничиваются против поля; положительной - парамагнетики (ПМ) и ферромагнетики (ФМ), они намагничиваются по полю. М. в. ДМ и ПМ мала по абс. величине, она слабо зависит от Н и то лишь в области очень сильных полей (и низких темп-р). Магнитная же индукция определяется как напряженностью, так и свойствами среды (вещества), характеризующимися относительной магнитной проницаемостью m, (или просто магнитной проницаемостью), которая показывает, во сколько раз проницаемость вещества больше или меньше проницаемости вакуума.
Магнитная индукция в среде (веществе) В = m m 0 Н, где m m 0 = m а – абсолютная магнитная проницаемость вещества. Чтобы понять магнитные свойства различных веществ, характеризуемые значением m, и, в частности, материалов, которые применяют для изготовления сердечников электромагнитных элементов разных типов, необходимо знать строение атомов и кристаллов твердых тел. Как известно, атом состоит из ядра и электронов, вращающихся вокруг ядра по орбитам. Круговой ток создает магнитный момент, (А× м2), определяемый формулой m = i S, где i — сила тока, А; S — площадь, обтекаемая током, м 2; поэтому вращающийся по орбите электрон обладает некоторым орбитальным магнитным моментом. Кроме того, при движении по орбите каждый электрон обладает свойством, близким к свойствам заряженного тела, вращающегося вокруг своей оси. Это свойство называют спином электрона. Спин электрона, эквивалентный круговому току, обусловливает спиновый магнитный момент. Протоны и нейтроны, входящие в ядро атома, тоже имеют некоторые магнитные моменты, но в сотни раз меньшие, чем электроны. Поэтому можно считать, что магнитные свойства атома определяются в основном магнитными свойствами его электронов (рисунок 1, а). В случае нескольких электронов полный, или собственный, магнитный момент атома определяется векторной суммой орбитальных и спиновых моментов с учетом их направления. Орбитальные и спиновые магнитные моменты могут иметь лишь одно из двух возможных направлений (согласное или противоположное). В том случае, если они направлены в противоположные стороны, магнитные моменты пары электронов взаимно компенсируются. Это имеет место в любой полностью заполненной оболочке, например, у атома гелия, изображенного на рисунок 1, б. Собственный магнитный момент такого атома в отсутствие внешнего поля равен нулю. ВОПРОС 3 Рассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости m. Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества. Опыт показывает, что все вещества, помещенные в магнитное поле, намагничиваются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера, согласно которой в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом (см. (109.2)) pm=ISn, модуль которого где I=en — сила тока, n — частота вращения электрона по орбите, S — площадь орбиты. Если электрон движется по часовой стрелке, то ток направлен против часовой стрелки и вектор рm (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона, как указано на рисунке. С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса Le, модуль которого, согласно где v = 2pn, pr2 = S. Вектор Le (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона. где величина Экспериментальное определение гиромагнитного отношения проведено в опытах Эйнштейна и де Гааза* (1915), которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое оказалось равным –(e/m). Таким образом, знак носителей, обусловливающих молекулярные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза бо2льшим, чем введенная ранее величина g (см. (131.4)). Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орбитальных моментов (см. (131.1) и (131.2)) электрон обладает собственным механическим моментом импульса Les, называемым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона Les, соответствует собственный (сотовый) магнитный момент рms, пропорциональный Les и направленный в противоположную сторону: Величина gs называется гиромагнитным отношением спиновых моментов. Проекция собственного магнитного момента на направление вектора В может принимать только одно из следующих двух значений: где ħ=h/(2p) (h—постоянная Планка), mb—магнетон Бора, являющийся единицей магнитного момента электрона.
В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома, следовательно, складывается из магнитных моментов входящих в его состав электронов и магнитного момента ядра (обусловлен магнитными моментами входящих в ядро протонов и нейтронов). Однако магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими пренебрегают. Таким образом, общий магнитный момент атома (молекулы) pa равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов: Эффектом Эйнштейна — де Хааза (эффект Эйнштейна — де Гааза) называется процесс получения телом вращательного момента импульса вдоль оси вращения, пропорционального приобретённой намагниченности. Эффект открыт в 1915 году Эйнштейном и нидерландским физиком В. де Хаазом. Эффект обратный эффекту Барнетта. Магни́тный моме́нт электрона, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина. В случае плоского контура с электрическим током магнитный момент вычисляется как , где Для произвольного замкнутого контура магнитный момент находится из:
где В общем случае произвольного распределения токов в среде:
где ВОПРОС 4 Атом в магнитном поле При внесении атома в магнитное поле с индукцией на электрон, движущийся по орбите, эквивалентной замкнутому контуру с током, действует момент сил
При этом изменяется орбитальный момент импульса электрона:
Аналогично изменяется вектор орбитального магнитного момента электрона:
Из этого следует, что векторы
Эта прецессия называется ларморовской прецессией. Угловая скорость этой прецессии Теорема Лармора: единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора Прецессия орбиты электрона в атоме приводит к появлению дополнительного орбитального тока, направленного противоположно току I:
и соответствующего ему наведенного орбитального магнитного момента где
ВОПРОС 5 Диамагнитный эффект возникает во всех веществах, но если молекулы вещества имеют собственные магнитные моменты, которые ориентируются по направлению внешнего магнитного поля и усиливают его, то диамагнитный эффект перекрывается более сильным парамагнитным эффектом и вещество оказывается парамагнетиком. Диамагнетиками называются вещества, магнитные моменты атомов которых в отсутствии внешнего поля равны нулю, т.к. магнитные моменты всех электронов атома взаимно скомпенсированы (например инертные газы, водород, азот, NaCl и др.). При внесении диамагнитного вещества в магнитное поле его атомы приобретают наведенные магнитные моменты. В пределах малого объема ΔV изотропного диамагнетика наведенные магнитные моменты Вектор намагниченности диамагнетика равен: , где n0 – концентрация атомов, Для всех диамагнетиков Парамагнетиками называются вещества, атомы которых имеют, в отсутствие внешнего магнитного поля, отличный от нуля магнитный момент К парамагнетикам относятся многие щелочные металлы, кислород, оксид азота NO, хлорное железо и др. В отсутствие внешнего магнитного поля намагниченность парамагнетика При внесении парамагнетика во внешнее магнитное поле происходит преимущественная ориентация собственных магнитных моментов атомов Закон Кюри — физический закон, описывает магнитную восприимчивость парамагнетиков, которая при постоянной температуре для этого вида материалов приблизительно прямо пропорциональна приложенному магнитному полю. Закон Кюри постулирует, что при изменении температуры и постоянном внешнем поле, степень намагниченности парамагнетиков обратно пропорциональна температуре: где в единицах Международной системе единиц (СИ): ВОПРОС 6 Ферромагнетики — вещества (как правило, в твёрдом кристаллическом или аморфном состоянии), в которых ниже определённой критической температуры (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов атомов или ионов (в неметаллических кристаллах) или моментов коллективизированных электронов (в металлических кристаллах). Иными словами, ферромагнетик — такое вещество, которое, при температуре ниже точки Кюри, способно обладать намагниченностью в отсутствие внешнего магнитного поля. Основной характеристикой процесса намагничивания является кривая намагничивания – зависимость магнитной индукции B в ферромагнетики от напряженности магнитного поля H
Гистерезис(от греч. hysteresis — отставание, запаздывание) явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность), неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля). Г. наблюдается в тех случаях, когда состояние тела в данный момент времени определяется внешними условиями не только в тот же, но и в предшествующие моменты времени. Оста́точная намагни́ченность — намагниченность, которую имеет ферромагнитный материал при напряжённости внешнего магнитного поля, равной нулю. В уравнениях обозначается как Величина остаточной намагниченности определяется точкой пересечения петли гистерезиса с осью магнитной индукции ферромагнетик Коэрцитивная сила — такое размагничивающее внешнее магнитное поле напряженностью МАГНИТНАЯ ДОМЕННАЯ СТРУКТУРА - совокупность макроскопич. областей (доменов)магнитоупорядоченного вещества, отличающихся, в зависимости от конкретного типа магн. упорядочения, направлением намагниченности М, вектора антиферромагнетизма L или направлениями М и L одновременно (а также размером, формой и др. особенностями, связанными, в частности, с кристаллографич. структурой образца и геометрией его поверхности). Закон Кюри — Вейса описывает магнитную восприимчивость ферромагнетика в области температур выше точки Кюри (то есть в парамагнитной области). Закон выражается следующей математической формулой
где При T = Tc магнитная восприимчивость стремится к бесконечности. При снижении температуры до точки Кюри и ниже возникает спонтанная намагниченность вещества.Во многих веществах закон Кюри — Вейса неприменим в окрестности точки Кюри, поскольку он основан на приближении среднего поля. В этих случаях критическое поведение описывается формулой
с критическим индексом Закон Кюри — Вейса выполняется также для антиферромагнетиков при температурах выше точки Нееля. В этом случае константа В сегнетоэлектриках связь между поляризуемостью сегнетоэлектрика и его температурой T в неполярной фазе вблизи точки Кюри, также может быть описана формулой, совпадающей с законом Кюри — Вейса где C и
ФЕРРОМАГНЕТИЗМ - магнитоупорядоченное состояние вещества, в к-ром большинство атомных магнитных моментов параллельны друг другу, так что вещество обладает самопроизвольной (спонтанной) намагниченностью. Ф. устанавливается при темп-ре Т ниже Кюри точки ТC в отсутствие внеш. магн. поля Н. В более широком смысле Ф. наз. совокупность физ. свойств вещества в указанном состоянии.
Ферриты (оксиферы) — химические соединения оксида железа Fe2O3 с оксидами других металлов, обладающие уникальными магнитными (ферримагнетики) свойствами, сочетающие высокую намагниченность и полупроводниковые или диэлектрические свойства, благодаря чему они получили широкое применение как магнитные материалы в радиотехнике, радиоэлектронике, вычислительной технике. &n
|
||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.018 с.) |



 . В качестве количественной характеристики магнитного состояния среды примем по определению величину намагниченности
. В качестве количественной характеристики магнитного состояния среды примем по определению величину намагниченности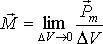
 представляет собой магнитный момент единицы объема среды. Намагниченность является локальной характеристикой среды, она определяется в каждой точке пространства и образует соответствующее векторное поле.
представляет собой магнитный момент единицы объема среды. Намагниченность является локальной характеристикой среды, она определяется в каждой точке пространства и образует соответствующее векторное поле. , где
, где  - порядковый номер этого тока в совокупности молекулярных токов объема, то легко получить:
- порядковый номер этого тока в совокупности молекулярных токов объема, то легко получить:
 - объемная концентрация элементарных молекулярных токов в рассматриваемой точке пространства, а
- объемная концентрация элементарных молекулярных токов в рассматриваемой точке пространства, а  - средний магнитный момент одного магнитного диполя.
- средний магнитный момент одного магнитного диполя.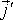 и силу тока
и силу тока  намагничения. Токи проводимости (с объемной плотностью
намагничения. Токи проводимости (с объемной плотностью  и силой тока
и силой тока 
 Однородная намагниченность.
Однородная намагниченность.
 Неоднородная намагниченность.
Неоднородная намагниченность.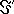 возникает объемная плотность
возникает объемная плотность  в магнитном веществе, ограниченную замкнутым контуром
в магнитном веществе, ограниченную замкнутым контуром  с выбранным положительным направлением обхода и ориентацией нормали к элементу площади ее поверхности. Ток намагничения определим соотношением
с выбранным положительным направлением обхода и ориентацией нормали к элементу площади ее поверхности. Ток намагничения определим соотношением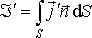
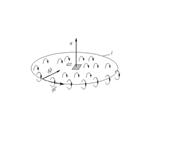 Молекулярные токи.
Молекулярные токи. в одну сторону и другую, тем самым не создавая результирующего тока намагничения. Для приграничных точек поверхности
в одну сторону и другую, тем самым не создавая результирующего тока намагничения. Для приграничных точек поверхности  , ориентация магнитного диполя относительно элемента
, ориентация магнитного диполя относительно элемента  описывается в среднем углом
описывается в среднем углом 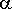 , то "ометаемой" площадкой
, то "ометаемой" площадкой  объем при перемещении на
объем при перемещении на 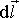 составит величину
составит величину 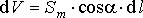 . Магнитные диполи в "ометаемом" объеме
. Магнитные диполи в "ометаемом" объеме 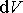 формируют ток намагничения
формируют ток намагничения
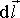 контура
контура  . Из соотношения
. Из соотношения  следует
следует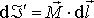

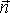 согласованы между собой, и его дифференциальный аналог (следствие классической теоремы Стокса):
согласованы между собой, и его дифференциальный аналог (следствие классической теоремы Стокса): 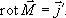
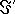 - сила молекулярного тока,
- сила молекулярного тока,  по замкнутому контуру в магнитной среде должна рассчитываться с учетом всех токов, которые условно разделены на ток проводимости
по замкнутому контуру в магнитной среде должна рассчитываться с учетом всех токов, которые условно разделены на ток проводимости  и ток молекулярный
и ток молекулярный 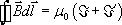

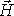 поля:
поля:

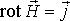

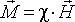
 - магнитная восприимчивость среды. При феноменологическом описании среды зависимость и, в частности, величина
- магнитная восприимчивость среды. При феноменологическом описании среды зависимость и, в частности, величина 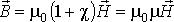



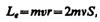

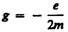 называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком «–», указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения v и r различны. Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.
называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком «–», указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения v и r различны. Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.


 Еще раз обратим внимание на то, что при рассмотрении магнитных моментов электронов и атомов мы пользовались классической теорией, не учитывая ограничений, накладываемых на движение электронов законами квантовой механики. Однако это не противоречит полученным результатам, так как для дальнейшего объяснения намагничивания веществ существенно лишь то, что атомы обладают магнитными моментами.
Еще раз обратим внимание на то, что при рассмотрении магнитных моментов электронов и атомов мы пользовались классической теорией, не учитывая ограничений, накладываемых на движение электронов законами квантовой механики. Однако это не противоречит полученным результатам, так как для дальнейшего объяснения намагничивания веществ существенно лишь то, что атомы обладают магнитными моментами.
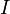 — сила тока в контуре,
— сила тока в контуре, 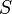 — площадь контура,
— площадь контура, 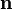 — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.
— единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.
 — радиус-вектор, проведенный из начала координат до элемента длины контура
— радиус-вектор, проведенный из начала координат до элемента длины контура 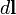
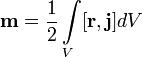
 — плотность тока в элементе объёма
— плотность тока в элементе объёма  .
.



 и
и  , и сама орбита прецессирует вокруг направления вектора
, и сама орбита прецессирует вокруг направления вектора  . На рисунке показано прецессионное движение электрона и его орбитального магнитного момента, а также дополнительное (прецессионное) движение электрона.
. На рисунке показано прецессионное движение электрона и его орбитального магнитного момента, а также дополнительное (прецессионное) движение электрона.
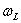 зависит только от индукции магнитного поля и совпадает с ней по направлению.
зависит только от индукции магнитного поля и совпадает с ней по направлению. 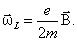

 :
: 
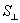 – площадь проекции орбиты электрона на плоскость, перпендикулярную вектору
– площадь проекции орбиты электрона на плоскость, перпендикулярную вектору  противоположен вектору
противоположен вектору 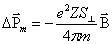
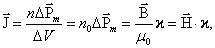
 – магнитная постоянная,
– магнитная постоянная,  –магнитная восприимчивость среды.
–магнитная восприимчивость среды.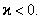 Таким образом, вектор
Таким образом, вектор  магнитной индукции собственного магнитного поля, создаваемого диамагнетиком при его намагничивании во внешнем поле направлен в сторону, противоположную
магнитной индукции собственного магнитного поля, создаваемого диамагнетиком при его намагничивании во внешнем поле направлен в сторону, противоположную  . (В отличие от диэлектрика в электрическом поле).
. (В отличие от диэлектрика в электрическом поле). , так как векторы
, так как векторы  разных атомов ориентированы беспорядочно.
разных атомов ориентированы беспорядочно.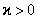 ) и находятся в пределах
) и находятся в пределах  , то есть примерно как и у диамагне тиков.
, то есть примерно как и у диамагне тиков.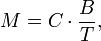
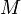 — получаемая намагниченность материала;
— получаемая намагниченность материала;  — магнитное поле, измеренное в Теслах;
— магнитное поле, измеренное в Теслах;  — абсолютная температура в Кельвинах;
— абсолютная температура в Кельвинах;  — постоянная Кюри данного материала. Это соотношение, полученное экспериментально П. Кюри, выполняется только при высоких температурах или слабых магнитных полях. В обратном случае — то есть при низких температурах или при сильных полях — намагниченность не подчиняется этому закону.
— постоянная Кюри данного материала. Это соотношение, полученное экспериментально П. Кюри, выполняется только при высоких температурах или слабых магнитных полях. В обратном случае — то есть при низких температурах или при сильных полях — намагниченность не подчиняется этому закону.
 . В технике часто считается, что намагниченность M это синоним для остаточной магнитной индукции B (они отличаются на магнитную постоянную
. В технике часто считается, что намагниченность M это синоним для остаточной магнитной индукции B (они отличаются на магнитную постоянную 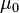 ,
,  ), поэтому остаточная намагниченность часто обозначается как
), поэтому остаточная намагниченность часто обозначается как  .
. , которое необходимо приложить к ферромагнетику, предварительно намагниченному до насыщения, чтобы довести до нуля его намагниченность
, которое необходимо приложить к ферромагнетику, предварительно намагниченному до насыщения, чтобы довести до нуля его намагниченность 
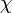 — магнитная восприимчивость, C — постоянная Кюри, зависящая от вещества, T — абсолютная температура в кельвинах, Tc — температура Кюри, К.
— магнитная восприимчивость, C — постоянная Кюри, зависящая от вещества, T — абсолютная температура в кельвинах, Tc — температура Кюри, К.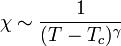
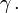 Однако при температурах
Однако при температурах 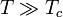 закон Кюри — Вейса выполняется, хотя в этом случае
закон Кюри — Вейса выполняется, хотя в этом случае  представляет температуру несколько больше действительной точки Кюри.
представляет температуру несколько больше действительной точки Кюри.
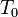 — константы, определяемые видом сегнетоэлектрика. Величина
— константы, определяемые видом сегнетоэлектрика. Величина