
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сколько тел и полей действует на данное тело, столько и сил (плюс силы трения и сопротивления, если они есть по условию задачи).Содержание книги
Поиск на нашем сайте
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ДИНАМИКУ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ АБСОЛЮТНО ТВЁРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ 1. Сделать чертёж к задаче, на котором нарисовать тело, вращающееся вокруг неподвижной оси, и все силы, действующие на него, с учётом точек приложения сил. 2. так как тело поступательно не движется, следовательно, относительно центра масс тела выполняется условие:
3. записать основное уравнение динамики вращательного движения тела относительно оси вращения:
4. решают полученную систему уравнений. (при необходимости её дополняют уравнениями движения.)
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ОПРЕДЕЛЕНИЕ МЕХАНИЧЕСКОЙ РАБОТЫ 1. установить, работу какой силы необходимо определить (это может быть как отдельная сила, так и результирующая многих сил). 2. работу этой силы можно определить либо: - по формуле работы механической силы, - по теореме о кинетической энергии, - по теореме о потенциальной энергии, - по закону изменения полной механической энергии. 3. по ходу решения может понадобиться определить угол между вектором силы и перемещением. В этом случае делается рисунок, на котором указывается сила, вектор перемещения и определяется этот угол. При необходимости определяется величина перемещения.
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ОПРЕДЕЛЕНИЕ МОЩНОСТИ Прежде всего надо разобраться какую мощность требуется определить: среднюю или мгновенную. Среднюю мощность можно определить по формулам:
Мгновенную мощность по формуле: N = Fvмгн .cosα, где vмгн – это мгновенная скорость тела
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ОПРЕДЕЛЕНИЕ КПД При определении КПД рекомендуется начинать решение задачи с определяющей формулы, при этом следует разобраться какая работа или мощность являются полезными, а какие затраченными.
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ ИМПУЛЬСА 1. сделать два рисунка, на которых изобразить ситуацию, рассматриваемую в задаче непосредственно до взаимодействия и сразу после взаимодействия. Здесь же указать направления векторов скоростей или импульсов всех тел системы. 2. Проанализировать все силы, действующие на тела системы в момент взаимодействия. - если система замкнута или взаимодействие происходит очень кратковременно (удар, разрыв снаряда, выстрел), то записать закон сохранения импульса для рассматриваемой системы в векторном виде:
- если система не замкнута, то записать закон изменения в виде:
3. Выбрать подходящую систему координат и спроектировать векторные уравнения на оси координат. (при этом следует помнить, что импульсы всех тел должны быть записаны относительно одной и той же системы координат (обычно относительно земли)), 4. решить полученную систему уравнений (при необходимости её дополнить уравнениями динамики или кинематики).
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ ЭНЕРГИИ 1. сделать рисунок, на котором указать начальное и конечное положения тела (или тел), а также его скорости в начальном и конечном положениях. Выбрать начальный уровень отсчёта потенциальной энергии (обычно он выбирается по самой нижней точке траектории тела). 2. Проанализировать все силы, действующие на тела системы за рассматриваемый промежуток времени. - если на тела системы действуют только консервативные силы ( - если на тела системы действуют неконсервативные силы, которые совершают работу над телами системы, то записать закон изменения полной механической энергии в виде:
(при этом следует помнить, что скорости всех тел и работы всех сил должны быть записаны относительно одной и той же системы координат (обычно относительно земли)). 3. расписать работы всех сил и полную механическую энергию в начальном и конечном положениях. Решить полученную систему уравнений (при необходимости её дополнить уравнениями динамики или кинематики).
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ О КИНЕТИЧЕСКОЙ ЭНЕРГИИ 1. сделать рисунок, на котором указать начальное и конечное положения тела (или тел), а также его скорости в начальном и конечном положениях. 2. Проанализировать все силы, действующие на тела системы за рассматриваемый промежуток времени. 3. записать теорему о кинетической энергии в виде (при этом следует помнить, что скорости всех тел должны быть записаны относительно одной и той же системы координат (обычно относительно земли)). 4. расписать работы всех сил и кинетическую энергию в начальном и конечном положениях. Решить полученную систему уравнений (при необходимости её дополнить уравнениями динамики или кинематики).
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ Если в задаче требуется найти работу консервативной силы (особенно 1. сделать рисунок, на котором указать начальное и конечное положения тела (или тел), а также выбрать начальный уровень отсчёта потенциальной энергии. 2. записать теорему о потенциальной энергии: 3. решить данное уравнение.
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ПРИМЕНЕНИЕ ЗАКОНОВ ИДЕАЛЬНОГО ГАЗА Если состояние газа не изменяется, то обычно используют уравнение Менделеева – Клапейрона. - Если состояние газа меняется, то либо для каждого состояния записывают уравнение Менделеева – Клапейрона, либо уравнения для каких – либо изопроцессов (если масса газа не изменяется).
Вследствие испарения с открытой поверхности жидкости над ней всегда находится её пар. Если между паром и жидкостью установится динамическое равновесие, то плотность пара над жидкостью и его давление (упругость) на меняются и для данной жидкости при данной температуре имеют максимальные значения. Такой пар называется насыщенным. Пар, давление и плотность которого меньше давления и плотности насыщенного пара, называется ненасыщенным. С достаточной точностью насыщенный и ненасыщенный пар подчиняются уравнению Менделеева-Клапейрона. Ненасыщенный пар можно перевести в насыщенный при изохорическом охлаждении или изотермическом сжатии. Температура при которой пар становится насыщенным в случае изохорического охлаждения, называется точкой росы. Задачи, в которых используется понятие влажности, принципиально почти не отличаются от задач об идеальном газе. К ним предлагается широкое использование таблиц упругости и плотности водяных паров, из которых находят дополнительные данные к тем, что заданы в условии задачи. Например, при заданной температуре ненасыщенного пара и его точке росы можно с помощью таблиц определить абсолютную и относительную влажности воздуха; при заданной температуре насыщающего пара таблица поможет найти его давление (упругость) и плотность при этой температуре. Если требуется найти массу сконденсировавшегося пара, то следует определить массу этого пара как разность масс до и после его частичной конденсации.
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ПРИМЕНЕНИЕ ЗАКОНОВ ЭЛЕКТРОМАГНЕТИЗМА
Здесь можно выделить задачи о взаимодействии однородного магнитного поля с проводником или контуром с током и движущимися заряженными частицами, а также задачи о явлении электромагнитной индукции и самоиндукции.
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.200.114 (0.006 с.) |

 ,
, ,
, или N = Fv .cosα, если тело движется равномерно.
или N = Fv .cosα, если тело движется равномерно. ,
, .
.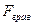 ,
,  ,
,  ,
,  ,
,  ) или все действующие на систему неконсервативные силы работы не совершают за рассматриваемый промежуток времени, то записать закон сохранения полной механической энергии для рассматриваемой системы в виде:
) или все действующие на систему неконсервативные силы работы не совершают за рассматриваемый промежуток времени, то записать закон сохранения полной механической энергии для рассматриваемой системы в виде:  ,
, .
. .
.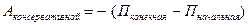 .
.


