
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила Кирхгофа для цепей постоянного тока
Первое правило Кирхгофа Алгебраическая сумма сил токов, сходящихся а узле, равна нулю, т.е. Второе правило Кирхгофа В любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма падений напряжений (произведений сил токов J на сопротивление R) на отдельных участках цепи этого контура равна алгебраической сумме ЭДС Ek, встречающихся в контуре:
Применяя законы Кирхгофа необходимо: 1. Определить число электрических узлов и независимых контуров в схеме Узлом называется место соединения трех и более проводников. Контур – это любая замкнутая цепь. Независимый контур – контур, который содержит хотя бы одну новую ветвь. Ветвь – участок цепи от узла до узла 2. Перед составлением уравнений произвольно выбрать и указать стрелками на чертеже: а) направление токов (если они не задана по условию задачи) во всех сопротивлениях, входящих в цепь, учитывая, что от узла до узла течёт один и тот же ток; б) направление обхода контура. 3. При составлении уравнений по первому закону Кирхгофа считать токи, подходящие к узлу, положительными, а токи, отходящие от узла - отрицательными. Число уравнений, составляемых по первому закону Кирхгофа, должно быть на единицу меньше числа узлов, содержащихся в цепи. 4. При составлении уравнений по второму правилу Кирхгофа следует считать: а) падение напряжения на участке цепи (т.е. произведение б) ЭДС Число независимых уравнений, которые могут быть составлены по второму закону Кирхгофа, равно числу независимых контуров, имеющихся в цепи. Для составления уравнений первый контур можно выбрать произвольно. Все следующие контуры следует выбирать таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь цепи, не участвовавшая ни в одном из ранее использованных контуров. Произвольно выбранное направление обхода по контурам не изменяется до конца решения задачи.
Если при решении уравнений, составленных вышеуказанным способом, получены отрицательные значения силы тока или напряжения, то это означает, что ток через данное сопротивление в действительности течет в направлении, противоположном выбранному.
ПЕРЕМЕННЫЙ ТОК Эффективное (или действующее) значение силы тока и напряжения Закон Ома для цепи переменного тока только с активным сопротивлением Закон Ома для цепи переменного тока с идеальной индуктивность Индуктивное сопротивление Закон Ома для цепи переменного тока с идеальной ёмкостью Емкостное сопротивление Закон Ома для цепи переменного тока с последовательно соединёнными активным сопротивлением, ёмкостью и индуктивностью
Полное сопротивление (или импеданс) цепи переменного тока Сдвиг фаз между силой тока и напряжением в цепи переменного тока ЭЛЕКТРОМАГНЕТИЗМ Уравнения Максвелла в интегральной форме (или полевые уравнения Максвелла) Первое уравнение Второе уравнение Третье уравнение Четвёртое уравнение
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.83.150 (0.006 с.) |
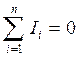

 ) входит в уравнение со знаком плюс, если направление тока в данном участке совпадает с выбранным направлением обхода контура; в противном случае произведение
) входит в уравнение со знаком плюс, если направление тока в данном участке совпадает с выбранным направлением обхода контура; в противном случае произведение  входит в уравнение со знаком плюс, если оно повышает потенциал в направлении обхода контура: т.е. если при обходе контура внутри источника тока приходится идти от минуса к плюсу, в противном случае ЭДС
входит в уравнение со знаком плюс, если оно повышает потенциал в направлении обхода контура: т.е. если при обходе контура внутри источника тока приходится идти от минуса к плюсу, в противном случае ЭДС 















