
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм решения задач по физике
В виду того, что универсальной методики решения задач не существует, ниже приводится примерный алгоритм, который облегчит Вам решение задач по физике.
Для успешного решения задач по физике необходимо: 1 Хорошо знать формулы и законы физики и уметь правильно их применять. 2 Знать размерность всех величин и уметь правильно переводить размерность величин из одной системы в другую. 3 Уметь определять тип задачи (т.е. к какому разделу физики она относится, и какой алгоритм решения можно применить к данной задаче.) 4 Иметь навык анализа полученной формулы и окончательного числового ответа.
К И Н Е М А Т И К А По кинематике материальной точки чаще всего встречаются задачи на следующие темы: 1 на составление уравнений поступательного движения, 2 на составление уравнений вращательного движения, 3 на определение средней скорости, 4 по кинематике сложного движения, 5 по кинематике относительного движения.
СХЕМА РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ МАТЕРИАЛЬНОЙ ТОЧКЕ 1 Сделать чертёж к задаче, на котором отметить начальные координаты тел и направления векторов их начальных скоростей и ускорений (начало координат обычно помещают в начальной точке движения тела или одного из тел. При выборе направлений координатных осей следует учитывать направление векторов перемещений, скоростей и ускорений тел).
2 Затем делают аналогичные чертежи для характерных моментов времени, о которых есть информация в условии задачи. 3 Записать уравнения движения для каждого тела в проекциях на оси координат сначала в общем виде для начального момента времени, а затем для характерных моментов времени, о которых есть информация в условии задачи.
При необходимости дополнить систему следующими уравнениями связи:
Следует помнить, что проекция вектора считается положительной, если вектор сонаправлен с положительным направлением оси координат, в противном случае проекция вектора считается отрицательной. Если вектор перпендикулярен оси координат, то его проекция на эту ось равна нулю 4 Решить полученную систему уравнений и найти решение задачи в общем (т.е. буквенном виде). Проанализировать полученное равенство. 5 Проверить размерность этого равенства и если она совпадает, подставить в окончательное уравнение числовые значения данных в условии задачи величин, предварительно переведя их в одну и ту же систему единиц. 6 Проанализировать полученный числовой ответ на физическую достоверность (то есть, скорость тела не может быть больше скорости света в вакууме, КПД двигателя не может быть больше 1 и т. д.)
СХЕМА РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ РАВНОМЕРНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ 1 Сделать чертёж к задаче, на котором отметить начальное положение материальной точки и направление её векторов скорости и центростремительного ускорения. 2 Затем делают аналогичные чертежи для характерных моментов времени, о которых есть информация в условии задачи. 3 Записать уравнение вращательного движения сначала в общем виде для начального момента времени, а затем для характерных моментов времени, о которых есть информация в условии задачи: φ = ± φ0 ± ω t, где: φ0 и φ – угол поворота радиус – вектора в начальный момент времени t = 0 c и в произвольный момент времени t. 4 При необходимости записать уравнения связи между угловыми и линейными величинами,
характеризующими кинематику материальной точки:
5 Решить полученную систему уравнений и найти решение задачи в общем (т.е. буквенном виде). Проанализировать полученное равенство. 6 Проверить размерность этого равенства и если она совпадает, подставить в окончательное уравнение числовые значения данных в условии задачи величин, предварительно переведя их в одну и ту же систему единиц. 7. Проанализировать полученный числовой ответ на физическую достоверность.
СХЕМА РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ СЛОЖНОГО ДВИЖЕНИЯ Если в задаче рассматривается движение тела одновременно относительно двух систем отсчёта, одна из которых условно принимается за «подвижную», а другая за «неподвижную» (например, человек идёт по движущемуся вагону или переплывает реку), то скорость или перемещение тела определяются по следующему правилу:
Вектор скорости тела относительно неподвижной системы координат равен векторной сумме скорости подвижной системы координат относительно неподвижной плюс скорость тела относительно подвижной системы координат. (аналогичное правило для перемещений).
где: скорость тела относительно неподвижной системы координат называется абсолютной скоростью скорость подвижной системы координат относительно неподвижной называется переносной скоростью скорость тела относительно подвижной системы координат называется относительной скоростью
СХЕМА РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ Если в задаче рассматривается движение двух независимых друг от друга тел, движущихся в одной и той же системе координат (например, движение встречных поездов и т.д.), то скорость или перемещение одного тела относительно другого определяются по следующему правилу: Вектор относительной скорости двух тел (аналогичное правило для перемещений)
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ОПРЕДЕЛЕНИЕ СРЕДНЕЙ СКОРОСТИ Следует различать: - среднюю скорость по перемещению - среднюю путевую скорость Средней скоростью по перемещению называется векторная величина, равная отношению перемещения тела за какой-либо промежуток времени к величине этого промежутка

Средней путевой скоростью называется скалярная величина, равная отношению пути пройденного телом за какой- либо промежуток времени к величине этого промежутка

особый случай: если тело на каком-либо участке пути движется всё время в одну сторону с одним и тем же по величине и направлению ускорением, то его среднюю путевую скорость можно найти по формуле:
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ДИНАМИКУ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ 1 Сделать чертеж к задаче, на котором: - нарисовать все тела, рассматриваемые в задаче, - нарисовать все силы, действующие на каждое тело, и, если возможно, указать направления ускорений каждого тела. 2. Для каждого тела записать второй закон Ньютона сначала в векторном виде - для каждого тела выбрать удобную систему координат (начало координат обычно помещают в центре тяжести тела, а одну из координатных осей направляют по вектору ускорения этого тела),
- для каждого тела расписывают своё векторное уравнение в проекциях на каждую ось с учётом знаков проекций сил.
3. Решают полученную систему уравнений. (необходимо помнить, что число уравнений должно быть равно числу неизвестных. Если уравнений динамики окажется не достаточно, то полученную систему дополняют уравнениями кинематики или законами изменения и сохранения).
Если в задаче требуется найти вес тела или его силу нормального давления, то следует помнить, что по третьему закону Ньютона они равны по величине, но противоположны по направлению силе реакции опоры.
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ДИНАМИКУ РАВНОМЕРНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ 1 Сделать чертёж к задаче, на котором нарисовать тело, движущееся по окружности, и все силы, действующие на него. 2. следует помнить, что тело движется равномерно по окружности постоянного радиуса только в том случае, если равнодействующая всех сил, действующих на тело, направлена по радиусу к центру этой окружности. Эта сила сообщает телу центростремительное ускорение, которое так же направлена к центру окружности, поэтому: - ось ОХ направляют по направлению центростремительного ускорения, (то есть к центру окружности, по которой оно движется). - записывают второй закон Ньютона сначала в векторном виде 3. решают полученную систему уравнений. (при необходимости её дополняют уравнениями движения с учётом, что Чтобы правильно определить количество сил, действующих на тело, необходимо придерживаться следующего правила:
|
|||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.229.253 (0.027 с.) |
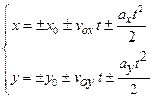 ,
,  ,
, - если движение равноускоренное,
- если движение равноускоренное, - если движение равнозамедленное.
- если движение равнозамедленное. ω =
ω = 






 равен векторной разности их абсолютных скоростей.
равен векторной разности их абсолютных скоростей. - скорость второго тела относительно первого
- скорость второго тела относительно первого - перемещение второго тела относительно первого
- перемещение второго тела относительно первого (величина векторная)
(величина векторная)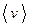 (величина скалярная)
(величина скалярная)




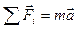 , а затем в проекциях на оси координат, для чего сначала:
, а затем в проекциях на оси координат, для чего сначала: , а затем в проекциях на оси координат, где
, а затем в проекциях на оси координат, где 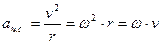 .
. ,
,  .
.


