
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розглянемо подію: А – власники 4-х квитків: 2 хлопчика і 2 дівчинки.
За формулою числа сполучень
Ймовірність того, що власниками 4-х квитків будуть 2 хлопчики і 2 дівчинки дорівнює:
Приклад 2. По цілі зроблено 20 пострілів, причому зафіксовано 18 влучень. Знайти відносну частоту влучень в ціль. Розв’язання. Нехай подія А – влучення в ціль. Всього було зроблено
Приклад 3. Два лиця А і В домовилися зустрітися в визначеному місці, при цьому кожний з’являється туди в любий момент часу між 11 і 12 годинами і дожидає на протязі 20 хвилин. Якщо партнер до цього часу ще не прийшов або вже покинув домовлене місце, зустріч не відбулася. Знайти ймовірність того, що зустріч відбудеться.
Площа g дорівнює площі квадрата без суми площ двох кутових не замальованих трикутників.
Приклад 4. В групі 25 студентів. Необхідно вибрати старосту, його замісника і профорга. Скільки існує способів це зробити? Розв’язання. Групування по 3 чоловіки з 25 можна здійснити
Приклад 5. Потяг має 5 вагонів, які можна причепити в різному порядку. Скільки існує варіантів сформувати потяг з даної кількості вагонів. Розв’язання. Кожний варіант формування потягу відрізняється тільки місцем розташування вагонів, тт. маємо задачу на перестановки з 5 елементів
Приклад 6. Скількома способами можна вибрати 3 фарби з 7, що є в наявності. Розв’язання. Шукане число способів визначається комбінаціями з 7 елементів по 3 елементи. Отже,
Приклад 7. Серед 15 мікрокалькуляторів, що наявні в обчислювальній лабораторії, лише 6 нових, а інші – були у вжитку. Навмання узято три мікрокалькулятори. Яка ймовірність, що усі вони виявляться новими?
Розв'язання. Розглянемо події: А — перший з узятих мікрокалькуляторів новий; В — другий мікрокалькулятор новий; С — третій мікрокалькулятор новий. Тоді Ймовірність того, що другий мікрокалькулятор буде новий, за умови, що першим уже був відібраний новий мікрокалькулятор, тобто умовна ймовірність події В, дорівнює
Ймовірність того, що третім буде відібраний новий мікрокалькулятор за умови, що уже відібрано два нових мікрокалькулятори, тобто умовна ймовірність події С, дорівнює
Шукана ймовірність того, що всі три відібраних мікрокалькулятори виявляться новими, дорівнює
Приклад 8. Три стрільці здійснюють по одному пострілу в ціль незалежно один від одного. Ймовірності влучення в ціль для кожного з них рівні відповідно 0,7; 0,8; 0,9. Знайти ймовірність того, що: а) у ціль потрапить тільки один стрілець; б) у ціль потраплять тільки два стрілці; в) у ціль потрапить хоча б один стрілець. Розв'язання. а) Розглянемо такі події: А1 — перший стрілець потрапив у ціль; А2 — другий стрілець потрапив у ціль; А3 — третій стрілець потрапив у ціль; Ā1 — перший стрілець не потрапив у ціль; Ā2 — другий стрілець не потрапив у ціль; Ā3 — третій стрілець не потрапив у ціль. За умовою P(A1)=0,7; P(A2)=0,8; Р(А3)=0,9; P(Ā1)=1-0,7=0,3; Р(Ā2)=0,2; Р(Ā3)=0,1. Нехай подія В — потрапив тільки один стрілець. Тоді В = А1Ā2Ā3+ Ā1А2Ā3+ Ā1Ā2А3 Звідси у силу умисності подій-доданків і незалежності подій-співмножників
С= А1А2Ā3+А1Ā2А3+Ā1А2А3, Звідси в) Нехай подія D — потрапив хоча б один стрілець. Тоді протилежна подія D — не потрапив жоден з них, тобто: P(D) = 1-Р(D) = 1-0,006=0,994 Приклад 9. На зборку надійшло 40% деталей заводу №1, 50% деталей заводу №2 і 10% деталей заводу №3. Перший завод дає 1% браку, другий–0,1%, третій 0,3%. Беруть навмання одну деталь. Яка ймовірність того, що вона буде бракованою? Розв'язання. Подія А – деталь бракована. Події: B1 – деталь виготовлена заводом №1. B2 – деталь виготовлена заводом №2.
B3 – деталь виготовлена заводом №3. Знайдемо ймовірності появи кожної з подій:
Сума ймовірностей усіх подій повинна дорівнювати 1, тому що події утворюють повну групу. Умовні ймовірності появи бракованої деталі (у залежності від заводу виробника) відповідно рівні:
За формулою повної ймовірності знайдемо ймовірність появи бракованої деталі:
Приклад 10. У наявності є 10 урн. У 3-х з них 4 білі, 6 чорних куль. У 5-ти – 7 білих, 3 чорні кулі. У 2-х – 2 білі, 8 чорних куль. Навмання узята куля виявилася білою. Яка ймовірність того, що вона взята з 3-ої групи урн? Розв'язання. Подія А – куля біла. Події: B1 – куля узята з першої групи урн. B2 – куля узята з другої групи урн. B3 – куля узята з третьої групи урн. Знайдемо ймовірність появи кожної з подій:
Обчислимо умовні ймовірності появи білої кулі:
Знайдемо ймовірність появи білої кулі:
За формулою Бейєса визначимо шукану ймовірність:
Повторення випробувань Формула Бернуллі. Ймовірність того, що в n незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює р Pn (k)= При великих значеннях n використовують теореми Лапласа. Число k 0 (настання подій А в n незалежних випробувань) називається найімовірнішим, якщо ймовірність того, що подія А настане у k 0 разів перевищує ймовірності інших можливих результатів.
Локальна теорема Лапласа. Ймовірність того, що в n незалежних випробувань, у кожному з яких ймовірність появи події дорівнює р
де При x>4, Інтегральна теорема Лапласа. Ймовірність того, що в n незалежних випробувань, у кожному з яких ймовірність появи події дорівнює р
При При великому числі випробувань n при малій ймовірності появи р події в кожнім окремому випробуванні для підрахунку ймовірності використовують формулу Пуассона:
Приклад 11. Ймовірність улучення в мішень при одному пострілі дорівнює 0,4. Знайти ймовірність 3-х улучень при 5-ти пострілах. Розв'язання. За формулою Бернуллі визначимо шукану ймовірність
Приклад 12. На підприємстві75% усієї продукції – продукція вищої якості. Знайти ймовірність того, що в партії зі 150 виробів: а) 100 виробів виявиться вищої якості; б) не менше 50 виробів виявиться вищої якості. Розв'язання. а) Скористаємося локальною теоремою Лапласа: n=150, k=100, p=0,75. Подія А – поява виробу відмінної якості.
за таблицею (Додаток 1) визначимо Р(А)=Р150(100) б)
Р100(50,150)
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.200.136 (0.028 с.) |

 ,
,  .
. обчислимо:
обчислимо: ;
; 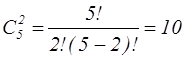 .
. .
. .
. =20 пострілів, з них
=20 пострілів, з них  =18 влучень. Тоді відносна частота влучень в ціль за формулою (1.2) дорівнює
=18 влучень. Тоді відносна частота влучень в ціль за формулою (1.2) дорівнює .
. Розв’язання. Позначимо моменти приходу в визначене місце лиць А і В через
Розв’язання. Позначимо моменти приходу в визначене місце лиць А і В через  і
і 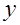 . В прямокутній системі координат
. В прямокутній системі координат  візьмемо за початок відліку 11 годин, а за одиницю вимірювання –1 год. За умовою
візьмемо за початок відліку 11 годин, а за одиницю вимірювання –1 год. За умовою 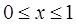 ,
,  . Цим нерівностям задовольняють координати любої точки, що належить квадрату
. Цим нерівностям задовольняють координати любої точки, що належить квадрату 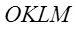 зі стороною 1. Нехай подія
зі стороною 1. Нехай подія  – зустріч двох лиць – відбудеться, якщо різниця між
– зустріч двох лиць – відбудеться, якщо різниця між  і
і  не перевищує
не перевищує  часу (по абсолютній величині), тт.
часу (по абсолютній величині), тт. 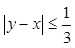 . Розв’язком останньої нерівності є смуга
. Розв’язком останньої нерівності є смуга  , що знаходиться в середині квадрата (площа g) (рис.1). За формулою (13) маємо
, що знаходиться в середині квадрата (площа g) (рис.1). За формулою (13) маємо .
. способами. Але серед вибраних 3 - х студентів теж важливо розподілення посад, а це можна зробити
способами. Але серед вибраних 3 - х студентів теж важливо розподілення посад, а це можна зробити  способами. Тому маємо задачу на розміщення
способами. Тому маємо задачу на розміщення


 .
.

 .
. б) Нехай подія С — потраплять тільки дві стрільці. Тоді
б) Нехай подія С — потраплять тільки дві стрільці. Тоді




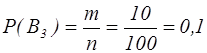


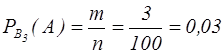
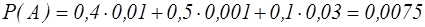 .
.


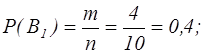

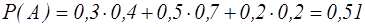
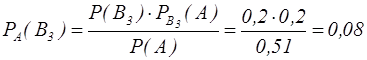
 , подія наступить рівно k разів (все рівно, в якій послідовності):
, подія наступить рівно k разів (все рівно, в якій послідовності): , де
, де 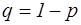 .
. .
.

 - функція Лапласа, обумовлена в таблиці (Додаток 1).
- функція Лапласа, обумовлена в таблиці (Додаток 1). .
. де
де
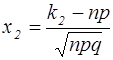 .
. - функція Лапласа, обумовлена у таблиці (Додаток 2).
- функція Лапласа, обумовлена у таблиці (Додаток 2). ,
,  .
. де
де  .
.

 тоді:
тоді:
 де
де


 отже:
отже: 0,5-(-0,5)=1.
0,5-(-0,5)=1.


