Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки та контрольні завданняСтр 1 из 6Следующая ⇒
МЕТОДИЧНІ ВКАЗІВКИ ТА КОНТРОЛЬНІ ЗАВДАННЯ ДО ВИКОНАННЯ САМОСТІЙНОЇ РОБОТИ ДЛЯ СТУДЕНТІВ ОЧНОЇ ФОРМИ НАВЧАННЯ «ТЕОРІЯ ЙМОВІРНОСТЕЙ ТА МАТЕМАТИЧНА СТАТИСТИКА»
економічний факультет
Мелітополь, 2004 р. Розробив: к.т.н. Назарова О.П. к.т.н., доц.. Рубців М.О.
Методичні вказівки розглянуті й схвалені на засіданні
кафедри протокол № _ _8_ _ від "_ __15_ __" травня 2004р.
Рецензент__________________к.е.н., доц. Арестєнко Т.В.
Рекомендовані до множення методичною комісією факультету "_ ___ _"_ _____ 2004р. протокол № ____.
ЗМІСТ
ВСТУП У зв’язку з тим, що в останні часи відбуваються значні зміни в переплануванні багатьох курсів фундаментальних дисциплін, (в тому числі і в курсі з вищої математики) пов’язані з ринковими відносинами і появою інших спеціальностей, тому багато вивчає мого матеріалу виноситься на самостійну роботу. В цілях надання допомоги студентам й інтенсифікації самостійної роботи програмою з курсу вищої математики передбачено виконання самостійної роботи по темі: “Теорія ймовірностей та математична статистика”. Мета методичних рекомендацій – засвоєння теоретичного матеріалу, набуття практичних навичок при розв’язанні задач за вказаною тематикою. В цілому це дає змогу краще підготуватися до семестрового іспиту. Поняття, які містить самостійна робота “Теорія ймовірностей та математична статистика” є базовими і на їх основі та аналізі вивчатимуться інші дисципліни, будуть виконуватися курсові і дипломні роботи. Робота складається з з таких тем:
У результаті вивчення студент повинен засвоїти:
– обчислення ймовірностей простих і складних подій; – основні теореми складання і множення подій; – формулу повної ймовірності. Формули Бейеса; – методику обчислення повторних випробувань; – числові характеристики випадкових величин (дискретних і неперервних); – обчислення функції розподілу випадкової величини. Знати алгоритми статистичних методів: – вибіркового методу; – кореляційного аналізу, МНК; – дисперсійного аналізу. Робота виконується на листах паперу формату А4. Зразок титульного листа наведено у додатку 6. Розділ 1. ТЕОРІЯ ЙМОВІРНОСТЕЙ Елементи теорії ймовірностей
Основні поняття Подія (А, В, С) – це будь-який факт, що може відбутися чи не відбутися в результаті випробування. Подія називається вірогідною, якщо за даного комплексу умов вона обов'язково відбудеться. Подія називається неможливою, якщо за даного комплексу умов вона ніколи не відбудеться. Подія називається випадковою, якщо за визначеного комплексу умов вона може відбутися чи не відбутися. Кілька подій утворюють повну групу (єдино можливі), якщо в результаті випробування хоча б одна з них відбудеться. Кілька подій називаються несумісними, якщо поява однієї з них виключає можливість появи іншої. Події називаються сумісними, якщо поява однієї не виключає появу інших. Події називаються рівноможливими, якщо немає підстави вважати, що одна з них більш можлива, ніж інша. Ймовірністю події називається відношення числа m сприятливих для даної події результатів до числа n усіх, утворюючих повну групу, несумісних і рівноможливих результатів Для будь-якої події де P(A)=0 – ймовірність неможливої події, P(A)=1 – ймовірність появи вірогідної події. Статистичною ймовірністю події А називається відносна частота появи цієї події в
де Одним з недоліків класичного означення ймовірності, обмежуючим його застосування, є те, що воно передбачає кінцеве число можливих результатів випробувань. Якщо позначити міру (довжину, площу, об’єм) області через mes, то геометричною ймовірністю події А називається відношення міри області сприятливої появі події А до міри усієї області, тт.
де g – фігура, сприятлива появі події А; G – фігура, на яку навмання кидається точка.
Елементи комбінаторики Для підрахунку числа появи подій використовують елементи комбінаторики. Сполука – це групи, утворені з яких-небудь предметів. Предмети, з яких утворені сполуки, називаються елементами. Найбільш важливі: перестановки, розміщення, комбінації. Розміщеннями з n елементів по m називаються такі сполуки, кожна з яких містить m елементів, узятих з даних n елементів, і які відрізняються одна від одної або порядком елементів, або самими елементами.
Перестановками з n елементів по n називаються розміщення з n, узяті по n ті що різняться тільки порядком елементів. Pn=n! Комбінації з n елементів по m називаються такі сполуки, кожна з яких містить m елементів, узятих з даних n елементів, і які відрізняються одна від одної самими елементами.
Повторення випробувань Формула Бернуллі. Ймовірність того, що в n незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює р Pn (k)= При великих значеннях n використовують теореми Лапласа. Число k 0 (настання подій А в n незалежних випробувань) називається найімовірнішим, якщо ймовірність того, що подія А настане у k 0 разів перевищує ймовірності інших можливих результатів.
Локальна теорема Лапласа. Ймовірність того, що в n незалежних випробувань, у кожному з яких ймовірність появи події дорівнює р
де При x>4, Інтегральна теорема Лапласа. Ймовірність того, що в n незалежних випробувань, у кожному з яких ймовірність появи події дорівнює р
При При великому числі випробувань n при малій ймовірності появи р події в кожнім окремому випробуванні для підрахунку ймовірності використовують формулу Пуассона:
Приклад 11. Ймовірність улучення в мішень при одному пострілі дорівнює 0,4. Знайти ймовірність 3-х улучень при 5-ти пострілах. Розв'язання. За формулою Бернуллі визначимо шукану ймовірність
Приклад 12. На підприємстві75% усієї продукції – продукція вищої якості. Знайти ймовірність того, що в партії зі 150 виробів: а) 100 виробів виявиться вищої якості; б) не менше 50 виробів виявиться вищої якості. Розв'язання. а) Скористаємося локальною теоремою Лапласа: n=150, k=100, p=0,75. Подія А – поява виробу відмінної якості.
за таблицею (Додаток 1) визначимо Р(А)=Р150(100) б)
Р100(50,150) Види рядів розподілу Генеральна сукупність - уся група об'єктів, що підлягають вивченню.
Вибірка - частина об'єктів генеральної сукупності, що потрапили на перевірку або дослідження Обсяг генеральної сукупності (вибірки ) - число елементів генеральної сукупності (вибірки): N,(n). Варіант - кожне окреме значення ознаки ( Частота - число, що показує, скільки разів зустрічається кожни варіант Статистичний ряд розподілу – упорядкована статистична сукупність. Ранжирований ряд – ряд чисел, що знаходиться в порядку зростання або спадання. Варіаційний ряд - ранжирований у порядку зростання або спадання ряд варіантів з відповідними їм частотами. Дискретний ряд - ряд, у якому окремі значення ознаки (варіанти) відрізняються одне від одного на деяку скінчену величину. Неперервний ряд (інтервальний) – ряд, у якому значення ознаки відрізняються одне від одного на яку завгодно малу величину. Статистичним інтервальним розподілом називається відповідність між інтервалами вибірки, частотами і відносними частотами. Відносною частотою
к – кількість інтервалів. При переході від інтервального ряду розподілу до дискретного припускають, що частоти згруповані в центрах інтервалів:
Атрибутивний ряд – ряд, у якому значення ознаки не має кількісного вираження.
Полігон відносних частот - ламана, яка з'єднує точки Діаграма - значення ознаки, виражене в процентному відношенні. Емпіричною функцією розподілу випадкової величини Х називається функція
де nx - число спостережень вибірки, менших за х Властивості: 1. Значення 2. 3.
Алгоритм вибіркового методу 1) Визначення розмаху вибірки: 2) побудова ранжированого ряду; 3) визначення кількості інтервалів: формула Стерджеса
4) обчислення кроку (довжини) інтервалів:
6) побудова дискретного ряду розподілу, полігона; 7) обчислення числових характеристик: середнього значення, дисперсії, середнього квадратичного відхилення, моди, медіани, коефіцієнта варіації, асиметрію, ексцес; 8) зробити висновок.
Приклад 15. Отримані вибіркові дані про врожайність зернових культур (ц/га) по господарствах Запорізької області за 2003 рік:
Використовуючи вибірковий метод: 1. визначити розмах вибірки; побудувати: 2. ранжирований ряд; 3. інтервальний ряд, гістограму; 4. дискретний ряд, полігон; 5. обчислити числові характеристики: 6. зробити висновок на підставі отриманих числових характеристик. Розв'язання. Обсяг вибірки (кількість елементів): 1. Визначимо максимальний і мінімальний варіант вибірки:
Розмах вибірки обчислимо за формулою:
2. Побудуємо ранжирований ряд, розташувавши значення вибірки в зростаючому чи спадному порядку:
3. Для побудови інтервального ряду розподілу визначимо кількість інтервалів розбивки за формулою:
Крок інтервалу визначаємо за формулою:
Складемо інтервальний ряд розподілу
Для отриманого ряду розподілу побудуємо гістограму відносних частот 4. Для переходу до дискретного ряду розподілу, припускаємо, що частоти згруповані в центрах інтервалів
Побудуємо полігон відносних частот (зобразимо на гістограмі). 1. Обчислимо числові характеристики вибірки даних, для чого побудуємо таблицю:
- середнє значення:
- дисперсію:
- виправлену дисперсію:
- середнє квадратичне відхилення:
- коефіцієнт варіації:
- моду:
- медіану:
- асиметрію:
- ексцес:
Висновок: У цілому по господарствах Запорізької області середня врожайність зернових культур складає 15,51-22,3 (ц/га),
Кореляційний аналіз Функціональним називають зв'язок між ознаками, при якому кожному значенню однієї змінної відповідає чітко окреслене значення іншої змінної. Кореляційним (статистичним) зв'язком називається такий зв'язок, при якому чисельному значенню однієї змінної відповідає кілька значень іншої. Кореляційною залежністю y від x називається така залежність, при якій зміни випадкової величини x спричинюють зміни середнього значення змінної y ( Вибірковим коефіцієнтом кореляції називається число:
де
Властивості коефіцієнта кореляції: a) абсолютна величина коефіцієнта кореляції не перевищує 1
b) якщо
c) якщо d) чим ближче e) якщо
Рівняння лінійної регресії Параметри лінійної регресії дорівнюють:
Перевірка гіпотези про значимість коефіцієнта кореляції. Гіпотеза а) Визначають значення критерію, що спостерігається
б) по таблиці Стьюдента (Додаток 3) визначають в) при
Метод найменших квадратів Лінійна залежність 1) Обчислюють середні для 2) Визначають параметри:
Параболічна залежність 1) Складають систему рівнянь:
2) Методом Крамера обчислюють параметри параболи:
Для досліджуваних видів функцій обчислюють середню погрішність:
Точніше та функція, у якої середня погрішність менше. Приклад 16. Задана залежність врожайності y (ц/га) від якості ґрунту x (у балах).
Знайти: -коефіцієнт кореляції; -рівняння лінійної регресії. -перевірити коефіцієнт кореляції на значимість. -рівняння лінійної, параболічної залежності (МНК), середню погрішність. Розв'язання. Для зручності обчислень складемо розрахункову таблицю:
Обчислимо середні значення для х і у:
Обчислимо середні квадратичні відхилення для х і у:
Обчислюємо коефіцієнт кореляції:
На підставі властивостей коефіцієнта кореляції робимо висновок. Оскільки r=0,62 >0, то між x і y сильний, зростаючий лінійний кореляційний зв'язок. Обчислюємо коефіцієнти лінійної регресії
Побудуємо на координатній площині задані пари точок і отримаєму пряму. Перевіримо коефіцієнта кореляції на значимість (критерій Стьюдента).
а) Обчислюємо значення критерію, що спостерігається
б) по таблиці Сть’юдента (Додаток 3) визначаємо
Оскільки
Метод найменших квадратів Для зручності складаємо таблицю:
1. Обчислимо середні значення для х і у:
2. Визначаємо параметри:
3. Складають систему рівнянь:
4. Обчислюють
4. Обчислюють параметри параболи:
Побудуємо графіки:
Для зручності складаємо таблицю:
Середня погрішність для прямій:
Середня погрішність для параболи:
Парабола точніше згладжує дані.
Розділ 3. ЗАВДАННЯ ДО САМОСТІЙНОЇ РОБОТИ Індивідуальні завдання
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.82.167 (0.182 с.) |

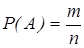 .
. ,
, проведених випробуваннях, тт.
проведених випробуваннях, тт. ,
, – статистична ймовірність події
– статистична ймовірність події  ;
;  – відносна частота події
– відносна частота події  ;
;  – число іспитів, в яких з’явилась подія
– число іспитів, в яких з’явилась подія  ;
; 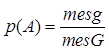 ,
, .
.
 , подія наступить рівно k разів (все рівно, в якій послідовності):
, подія наступить рівно k разів (все рівно, в якій послідовності): , де
, де 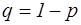 .
. .
.

 - функція Лапласа, обумовлена в таблиці (Додаток 1).
- функція Лапласа, обумовлена в таблиці (Додаток 1). .
. де
де
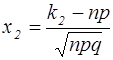 .
. - функція Лапласа, обумовлена у таблиці (Додаток 2).
- функція Лапласа, обумовлена у таблиці (Додаток 2). ,
,  .
. де
де  .
.

 тоді:
тоді:
 де
де


 отже:
отже: 0,5-(-0,5)=1.
0,5-(-0,5)=1.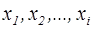 ).
).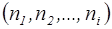 .
. (частістю) називають відношення частоти ni, щовідповідає значенню xi, до суми всіх частот (обсягу вибірки):
(частістю) називають відношення частоти ni, щовідповідає значенню xi, до суми всіх частот (обсягу вибірки): ,
, .
. Гістограма відносних частот - ступінчата фігура, що складається з прямокутників, основами яких служать інтервали
Гістограма відносних частот - ступінчата фігура, що складається з прямокутників, основами яких служать інтервали  , а висоти дорівнюють
, а висоти дорівнюють 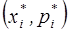 .
. ,
,
 - неспадна функція
- неспадна функція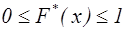
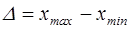 ;
;
 чи
чи  , (де n – обсяг вибірки)
, (де n – обсяг вибірки) , де xmin
, де xmin  , xmaх
, xmaх 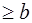
 .
.
 .
.

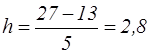
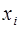





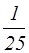



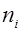


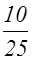





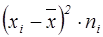






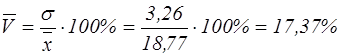




 . Причому в більшій частині господарств отриманий урожай 17,67(ц/га),
. Причому в більшій частині господарств отриманий урожай 17,67(ц/га),  . У цілому по області розсіювання за результатами врожайності значне
. У цілому по області розсіювання за результатами врожайності значне  . Спостерігається незначна правобічна скошеність у даних, незначна пласковершіність.
. Спостерігається незначна правобічна скошеність у даних, незначна пласковершіність. ), тобто
), тобто  .
. ,
,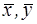 - вибіркові середні для
- вибіркові середні для  і
і 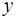 , тобто
, тобто 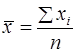 ,
,  .
. - вибіркові середньоквадратичні відхилення для
- вибіркові середньоквадратичні відхилення для 
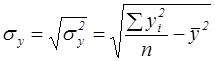 .
.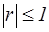
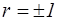 , то
, то  ;
; , то між
, то між  до
до 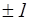 , тим сильніше лінійний зв'язок між
, тим сильніше лінійний зв'язок між 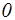 , тим він слабший;
, тим він слабший; , зв'язок між
, зв'язок між  , зв'язок – спадний.
, зв'язок – спадний.
 ,
, 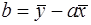 .
. : лінійного кореляційного зв'язку для даної генеральної сукупності немає.
: лінійного кореляційного зв'язку для даної генеральної сукупності немає. .
. .
. - нульову гіпотезу відкидають, при
- нульову гіпотезу відкидають, при 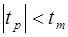 -
-  приймають.
приймають.

 ,
, 


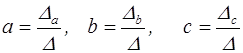



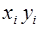
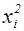


 ;
;  ; (n=4)
; (n=4) ;
; 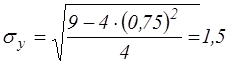 .
.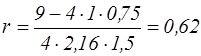 .
.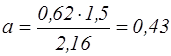 ;
; 


 - для даної генеральної сукупності лінійного кореляційного зв'язку немає.
- для даної генеральної сукупності лінійного кореляційного зв'язку немає.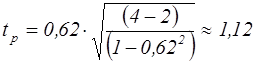 ,
, .
.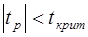 (1,12 < 4,30) нульову гіпотезу відкидаємо, тобто коефіцієнт кореляції для всієї генеральної сукупності не дорівнює нулю.
(1,12 < 4,30) нульову гіпотезу відкидаємо, тобто коефіцієнт кореляції для всієї генеральної сукупності не дорівнює нулю.

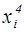
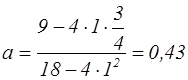 ,
, 






 Рівняння параболи має від:
Рівняння параболи має від:
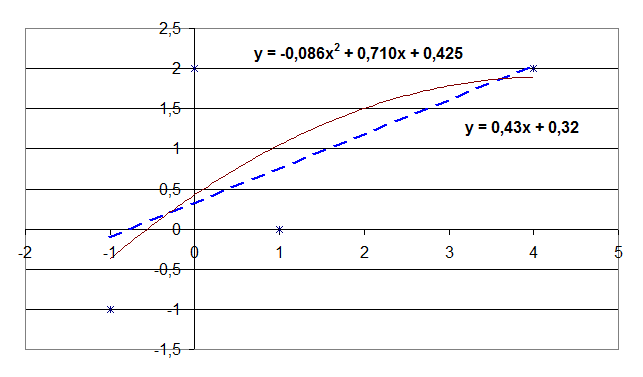 5. Обчислюють середню погрішність.
5. Обчислюють середню погрішність.